九年级数学上册试题 1.3二次函数的性质习题-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 1.3二次函数的性质习题-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 635.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 22:43:45 | ||
图片预览



文档简介
1.3二次函数的性质
一、单选题
1.在平面直角坐标系中,抛物线()与轴交于点,.若线段上有且只有7个点的横坐标为整数,则的取值范围是( )
A. B.
C. D.
2.关于二次函数的三个结论:①图象与轴的交点为;②对任意实数,都有与对应的函数值相等;③若,对应的的整数值有4个,则或.其中,正确结论的个数是( )
A.0 B.1
C.2 D.3
3.已知二次函数()的图象如图,则下列结论中正确的是( )
A. B.当时,y随x的增大而增大
C. D.3是方程的一个根
4.若抛物线(是常数)的图象经过第一、二、三象限,则的取值范围是( )
A. B. C. D.
5.已知二次函数与轴的交点是(1,0)和(3,0),关于的方程(其中)的两个解分别是和5,关于的方程(其中)也有两个整数解,这两个整数解分别是( )
A.1和4 B.2和5 C.0和4 D.0和5
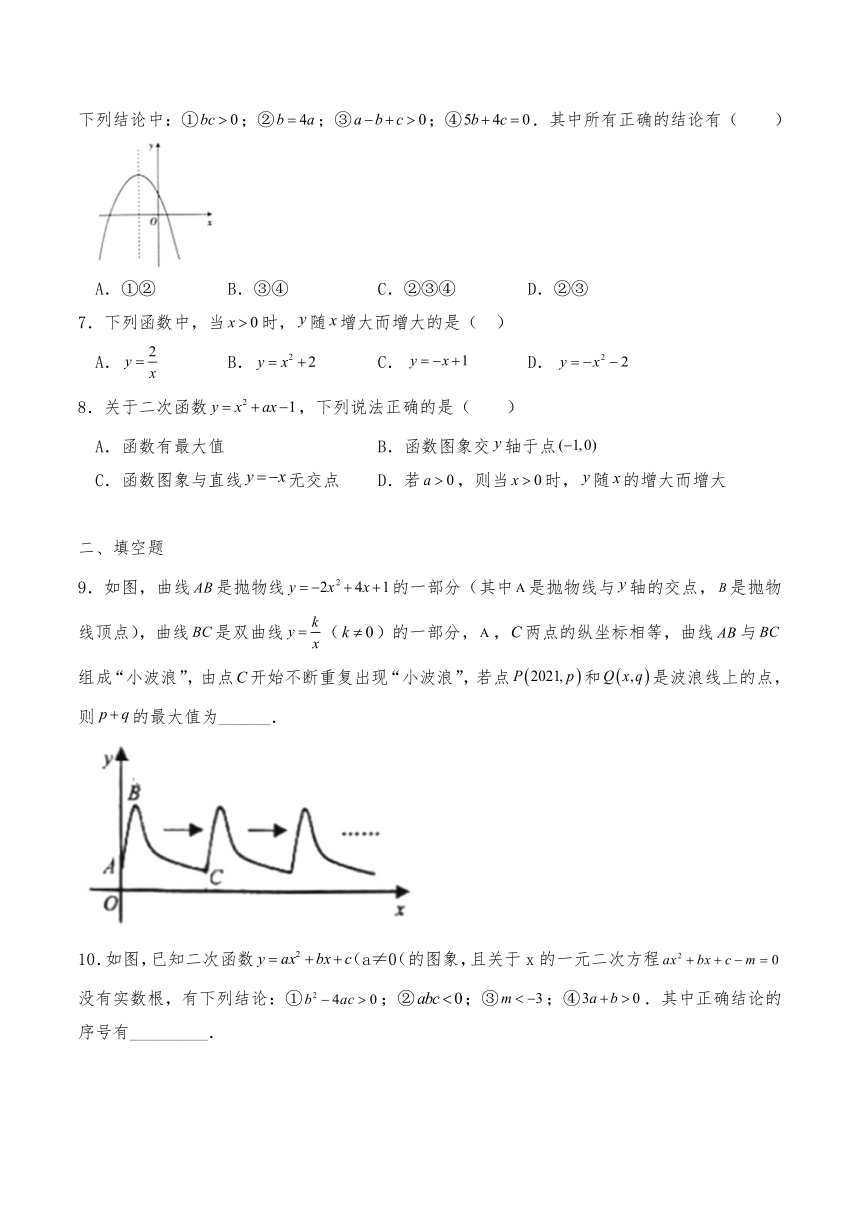
6.已知二次函数的图象如图所示,若方程的两个根为,,下列结论中:①;②;③;④.其中所有正确的结论有( )
A.①② B.③④ C.②③④ D.②③
7.下列函数中,当时,随增大而增大的是( )
A. B. C. D.
8.关于二次函数,下列说法正确的是( )
A.函数有最大值 B.函数图象交轴于点
C.函数图象与直线无交点 D.若,则当时,随的增大而增大
二、填空题
9.如图,曲线是抛物线的一部分(其中是抛物线与轴的交点,是抛物线顶点),曲线是双曲线()的一部分,,两点的纵坐标相等,曲线与组成“小波浪”,由点开始不断重复出现“小波浪”,若点和是波浪线上的点,则的最大值为______.
10.如图,已知二次函数(a≠0(的图象,且关于x的一元二次方程没有实数根,有下列结论:①;②;③;④.其中正确结论的序号有_________.
11.有一个二次函数的图象,甲、乙、丙三位同学分别说出了它的特点:
甲:对称轴是直线x=2;
乙:与x轴两个交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形的面积为3.请你写出满足上述全部特点的一个二次函数解析式_____.
12.已知抛物线与x轴交于不同的两点和与y轴的正半轴交于点C,如果,是方程的两个根且的面积为,求此抛物线解析式______.
13.已知二次函数的图象如图所示,则关于x的一元二次方程的根为___________.
14.抛物线y=ax2+bx+c(a,b,c为常数,a<0)的顶点为P(m,n),经过A(﹣1,0),B(3,0)两点,下列四个结论:
①bc>0;
②M(x1,y1),N(x2,y2)是抛物线上两点,若x1<x2,x1+x2>2,则y1<y2;
③关于x的方程a(x+1)2+bx=﹣c﹣b的解为x1=﹣2,x2=2;
④关于x的方程ax2+bx+c=a+n一定有两个不相等的实数根.其中正确的结论是_____(填写序号).
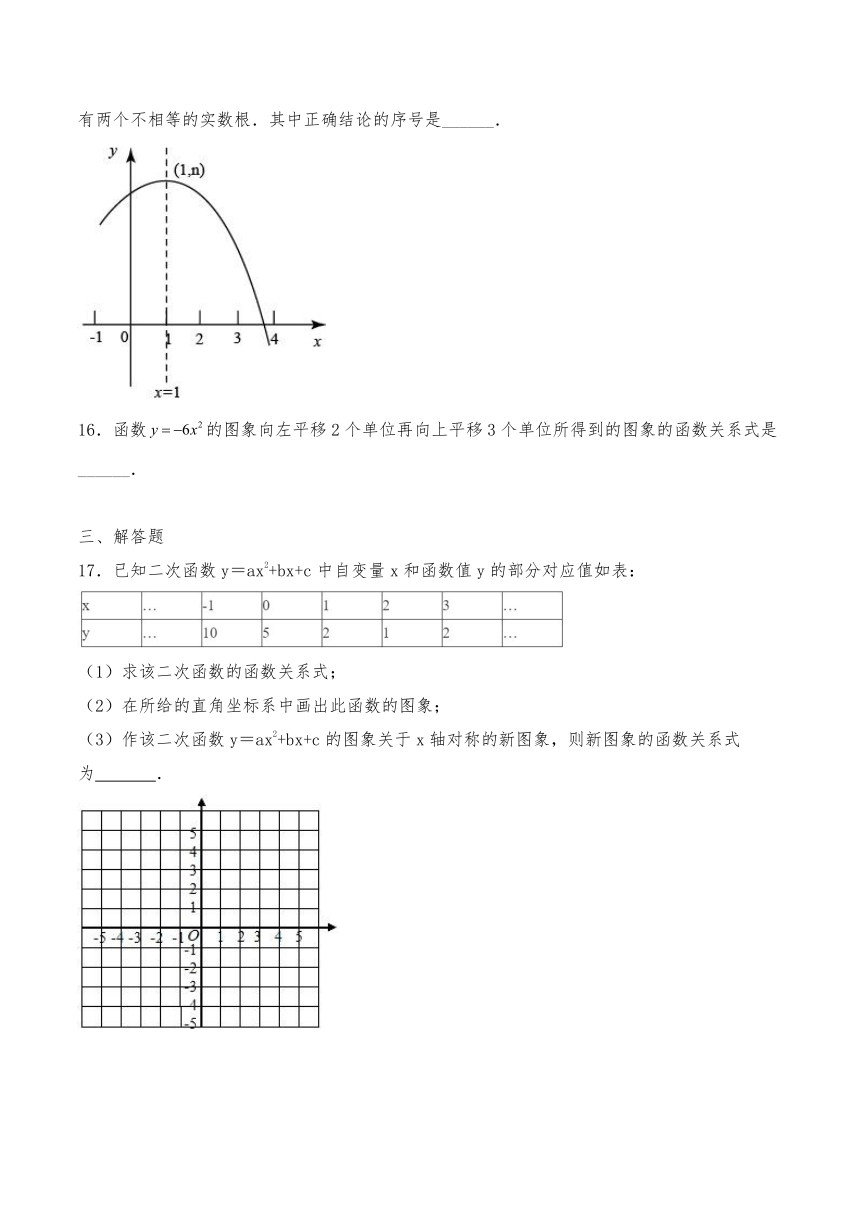
15.如图是抛物线的部分图象,其顶点为,且与轴的一个交点在点和之间下列结论:①;②;③;④关于的方程有两个不相等的实数根.其中正确结论的序号是______.
16.函数的图象向左平移2个单位再向上平移3个单位所得到的图象的函数关系式是______.
三、解答题
17.已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如表:
(1)求该二次函数的函数关系式;
(2)在所给的直角坐标系中画出此函数的图象;
(3)作该二次函数y=ax2+bx+c的图象关于x轴对称的新图象,则新图象的函数关系式为 .
18.在平面直角坐标系中,二次函数图象的表达式为,其中.
(1)若此函数图象经过点,求这个二次函数的表达式.
(2)若,为此二次函数图象上两个不同点.
①若,则,试求a的值.
②当,对任意的,都有,试求a的取值范围.
19.2020年是脱贫攻坚收官之年,为贯彻落实党中央全面建成小康社会的新部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.如果将农村家庭人均年纯收入8000元作为一个标准,该地区仅剩部分家庭尚未达标.2019年7月,为估计该地区能否在2020年底达到上述标准,统计了当时该地某一贫困家庭2019年1至6月的人均月纯收入,汇总如下:
月份代码 1 2 3 4 5 6
人均月纯收(元) 310 350 390 430 470 510
根据分析,发现该家庭人均月纯收入y与月份代码x之间具有一次函数关系(记2019年1月、2月、…、2020年1月、…分别为x=1,x=2,…,x=13,…,依此类推).
由于新冠肺炎疫情的影响,该家庭2020年第一季度每月人均月纯收入只有2019年12月人均月纯收入的三分之二.根据以上信息,完成以下问题.
(1)求该家庭人均月纯收入y与月份代码x之间的函数关系式;
(2)若疫情没有暴发,2020年底该家庭能否达到人均年纯收入8000元的标准
(3)2020年3月初开始,在当地党员干部的扶持下,该家庭的人均月纯收入y与月份代码x之间满足二次函数y=x2+bx+c的关系.若该家庭2020年12月人均月纯收入不低于1400元,求b的最小值.
(4)若以该家庭2020年3月人均月纯收入为基数,以后每月的增长率为a,为了使该家庭2020年底能达到人均年纯收入8000元的标准,a至少为多少 (结果保留两位小数)
(参考数据:≈62.81)(参考公式:1+x+x2+…+x9=;(1+a)10≈1+10a+45a2+120a3(|a|<0.15).
20.已知直线y=x+3分别交x轴和y轴于点A和B,抛物线y=ax2+bx+c经过点A和B,且抛物线的对称轴为直线x=﹣2.
(1)抛物线与x轴的另一个交点C的坐标为 ;
(2)试确定抛物线的解析式;
(3)在同一平面直角坐标系中分别画出两个函数的图象(请用2B铅笔或黑色水笔加黑加粗),观察图象,写出二次函数值小于一次函数值的自变量x的取值范围 .
21.关于x的二次函数与x轴有交点.
(1)求a的取值范围;
(2)当时,求抛物线与x轴两个交点间的距离.
22.如图,抛物线与轴交于(-1,0),(3,0)两点,直线与抛物线交于、两点,其中点的横坐标为2.
(1)求抛物线及直线的函数表达式;
(2)点是线段上的点(不与,重合)过作轴交抛物线于,若点的横坐标为,请用含的代数式表示的长.
23.已知二次函数的图象过点
(1)此二次函数的表达式,并用配方法将其化为的形式
(2)画出此函数的图象;
(3)借助图象,判断若,则 的取值范围是
24.求下列二次函数的顶点坐标:
(1)(配方法)
(2)(公式法)
25.某数学兴趣小组对函数的图象和性质进行探究,发现自变量的取值范围是全体实数,与的几组对应值列表如下:
… 0 1 2 3 …
… 0 …
(1)补全上表;
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程有 个实数根;
②关于的方程有2个实数根时,的取值范围是 .
③当取何值时,随的增大而增大?
26.已知抛物线的顶点坐标是,且过点.
求这个抛物线对应的函数表达式.
在所给坐标系中画出该函数的图象.
当取什么值时,函数值小于0
答案
一、单选题
B.D.D.D.C.C.B.D.
二、填空题
9..
10.①③④.
11.y=(x+1)(x﹣5).(答案不唯一).
12..
13.x1=-1,x2=3.
14.①③④.
15.①③④.
16..
三、解答题
17.
解:(1)由图表可知抛物线y=ax2+bx+c过点(1,2),(3,2),
∴对称轴为x==2;
∴顶点坐标为:(2,1),
∴设y=a(x﹣2)2+1,
将(0,5)代入可得:4a+1=5,
解得:a=1,
∴二次函数的解析式为:y=(x﹣2)2+1,即y=x2﹣4x+5,
所求二次函数的关系式为y=x2﹣4x+5.
(2)描点、连线画出函数图象如图:
;
(3)∵新图象与二次函数y=ax2+bx+c的图象关于x轴对称,
∴﹣y=x2﹣4x+5,
∴新图象的函数关系式为y=﹣x2+4x﹣5,
故答案为y=﹣x2+4x﹣5.
18.
(1)∵函数图象过点,
∴将点代入y=ax2+(a+1)x,
解得:a=﹣2,
;
(2)①∵(x1,y1),(x2,y2)为此二次函数图象上两个不同点
∴x1≠x2,
∵y1=y2,
∴ax12+(a+1)x1=ax22+(a+1)x2,
∴a(x1+x2)(x1﹣x2)=(a+1)(x2﹣x1),
a(x1+x2)=﹣(a+1),
∵x1+x2=4,
∴a=;
②函数y=ax2+(a+1)x的对称轴是,
∵x1>x2≥2,对任意的x1,x2都有,
当a>0时,无法满足条件;
当a<0时,,,
∴.
19.
(1)设人均月纯收入y与月份代码x之间的函数表达式为y=kx+m,
将数据(1,310),(2,350)代入得:解得
故函数表达式为y=40x+270.
(2)2020年1月对应x=13,2020年12月对应x=24,
则2020年该家庭的人均年纯收入为12个月人均月纯收入之和,
即(13×40+270)+(14×40+270)+…+(24×40+270)=270×12+40×(13+14+…+24)=12120>8000,
故2020年底该家庭能达到人均年纯收入8000元的标准.
(3)该家庭2019年12月人均月纯收入为:12×40+270=750(元)
该家庭2020年3月份的人均月纯收入为750×=500(元);
由题意得,152+15b+c=500,∴c=275-15b,又242+24b+c≥1400,∴b≥61,
故b的最小值为61.
(4)由题意,1000+500+500(1+a)+500(1+a)2+…+500(1+a)9≥8000,
得≥7000,其中(1+a)10≈1+10a+45a2+120a3(|a|<0.15),整理得:120a2+45a-4≥0.
令120a2+45a-4=0,得a=,∴a1≈0.07,a2≈-0.45,
故不等式的解集为a≤-0.45(舍去)或a≥0.07,∴a至少应为0.07.
20.
解:(1)∵直线y=x+3分别交x轴和y轴于点A和B,
∴点A(﹣3,0),点B(0,3),
∵抛物线的对称轴为直线x=﹣2.抛物线与x轴的另一个交点为C,
∴点C(﹣1,0),
故答案为(﹣1,0);
(2)∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),点C(﹣1,0),
∴,解得:,
∴二次函数的解析式为:y=x2+4x+3;
(3)如图所示:
当﹣3<x<0时,二次函数值小于一次函数值,
故答案为:﹣3<x<0.
21.
解:(1)∵二次函数y=(a-2)x2-8x+4与x轴有交点,
∴82-4×(a-2)×4=-16a+96≥0,a-2≠0,
解得,a≤6且a≠2;
(2)当a=3时,二次函数为:y=x2-8x+4,
设抛物线与x轴两个交点的坐标为(x1,0)、(x2,0),
则x1+x2=8,x1 x2=4,
.
22.
解:(1)把A(-1,0)、B(3,0)代入y=x2+bx-c得:
,
解得:,
∴解析式为:y=x2-2x-3,
把x=2代入y=x2-2x-3得y=-3,
∴C(2,-3),
设直线AC的解析式为y=kx+n,
把A(-1,0)、C(2,-3)代入得,
解得:,
∴直线AC的解析式为;
(2)∵点M在直线AC上,
∴M的坐标为(m,-m-1);
∵点F在抛物线y=x2-2x-3上,
∴F点的坐标为(m,m2-2m-3),
∴MF=(-m-1)-( m2-2m-3)=-m2+m+2.
23.
(1)把代入,
得,
解得:,
∴二次函数的表达式为:,
配方得:
(2)∵,
∴顶点坐标为(1,4),对称轴方程为x=1,
当y=0时,,
,
∴图像与x轴的交点坐标为(-1,0)(3,0),
又∵图像过点
可得下图:
(3)由图可得当时,则 的取值范围是,
故答案为:.
24.
解:(1)
,
∴顶点坐标为(2,-4)
(2),
∵,,,
∴,,
∴顶点坐标为顶点坐标为.
25.
解:(1)如下表:
(2)如图,
(3)①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当-2≤x≤0或x≥2时,y随x的增大而增大.
26.
解:(1)∵抛物线的顶点坐标是,
设抛物线的解析式为,
抛物线过点,
,
,
抛物线的解析式为;
(2)列表:
x … -3 -2 -1 0 1 …
y … 0 3 4 3 0 …
描点:在平面直角坐标系中描出点(-3,0),(-2,3),(-1,4),(0,3),(1,0)
连线:用平滑曲线连接,
(3)∵函数值小于,
∴函数图像再x轴下方,在-3左侧和1右侧,
当x<-3或x>1时,函数值小于.
一、单选题
1.在平面直角坐标系中,抛物线()与轴交于点,.若线段上有且只有7个点的横坐标为整数,则的取值范围是( )
A. B.
C. D.
2.关于二次函数的三个结论:①图象与轴的交点为;②对任意实数,都有与对应的函数值相等;③若,对应的的整数值有4个,则或.其中,正确结论的个数是( )
A.0 B.1
C.2 D.3
3.已知二次函数()的图象如图,则下列结论中正确的是( )
A. B.当时,y随x的增大而增大
C. D.3是方程的一个根
4.若抛物线(是常数)的图象经过第一、二、三象限,则的取值范围是( )
A. B. C. D.
5.已知二次函数与轴的交点是(1,0)和(3,0),关于的方程(其中)的两个解分别是和5,关于的方程(其中)也有两个整数解,这两个整数解分别是( )
A.1和4 B.2和5 C.0和4 D.0和5
6.已知二次函数的图象如图所示,若方程的两个根为,,下列结论中:①;②;③;④.其中所有正确的结论有( )
A.①② B.③④ C.②③④ D.②③
7.下列函数中,当时,随增大而增大的是( )
A. B. C. D.
8.关于二次函数,下列说法正确的是( )
A.函数有最大值 B.函数图象交轴于点
C.函数图象与直线无交点 D.若,则当时,随的增大而增大
二、填空题
9.如图,曲线是抛物线的一部分(其中是抛物线与轴的交点,是抛物线顶点),曲线是双曲线()的一部分,,两点的纵坐标相等,曲线与组成“小波浪”,由点开始不断重复出现“小波浪”,若点和是波浪线上的点,则的最大值为______.
10.如图,已知二次函数(a≠0(的图象,且关于x的一元二次方程没有实数根,有下列结论:①;②;③;④.其中正确结论的序号有_________.
11.有一个二次函数的图象,甲、乙、丙三位同学分别说出了它的特点:
甲:对称轴是直线x=2;
乙:与x轴两个交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形的面积为3.请你写出满足上述全部特点的一个二次函数解析式_____.
12.已知抛物线与x轴交于不同的两点和与y轴的正半轴交于点C,如果,是方程的两个根且的面积为,求此抛物线解析式______.
13.已知二次函数的图象如图所示,则关于x的一元二次方程的根为___________.
14.抛物线y=ax2+bx+c(a,b,c为常数,a<0)的顶点为P(m,n),经过A(﹣1,0),B(3,0)两点,下列四个结论:
①bc>0;
②M(x1,y1),N(x2,y2)是抛物线上两点,若x1<x2,x1+x2>2,则y1<y2;
③关于x的方程a(x+1)2+bx=﹣c﹣b的解为x1=﹣2,x2=2;
④关于x的方程ax2+bx+c=a+n一定有两个不相等的实数根.其中正确的结论是_____(填写序号).
15.如图是抛物线的部分图象,其顶点为,且与轴的一个交点在点和之间下列结论:①;②;③;④关于的方程有两个不相等的实数根.其中正确结论的序号是______.
16.函数的图象向左平移2个单位再向上平移3个单位所得到的图象的函数关系式是______.
三、解答题
17.已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如表:
(1)求该二次函数的函数关系式;
(2)在所给的直角坐标系中画出此函数的图象;
(3)作该二次函数y=ax2+bx+c的图象关于x轴对称的新图象,则新图象的函数关系式为 .
18.在平面直角坐标系中,二次函数图象的表达式为,其中.
(1)若此函数图象经过点,求这个二次函数的表达式.
(2)若,为此二次函数图象上两个不同点.
①若,则,试求a的值.
②当,对任意的,都有,试求a的取值范围.
19.2020年是脱贫攻坚收官之年,为贯彻落实党中央全面建成小康社会的新部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.如果将农村家庭人均年纯收入8000元作为一个标准,该地区仅剩部分家庭尚未达标.2019年7月,为估计该地区能否在2020年底达到上述标准,统计了当时该地某一贫困家庭2019年1至6月的人均月纯收入,汇总如下:
月份代码 1 2 3 4 5 6
人均月纯收(元) 310 350 390 430 470 510
根据分析,发现该家庭人均月纯收入y与月份代码x之间具有一次函数关系(记2019年1月、2月、…、2020年1月、…分别为x=1,x=2,…,x=13,…,依此类推).
由于新冠肺炎疫情的影响,该家庭2020年第一季度每月人均月纯收入只有2019年12月人均月纯收入的三分之二.根据以上信息,完成以下问题.
(1)求该家庭人均月纯收入y与月份代码x之间的函数关系式;
(2)若疫情没有暴发,2020年底该家庭能否达到人均年纯收入8000元的标准
(3)2020年3月初开始,在当地党员干部的扶持下,该家庭的人均月纯收入y与月份代码x之间满足二次函数y=x2+bx+c的关系.若该家庭2020年12月人均月纯收入不低于1400元,求b的最小值.
(4)若以该家庭2020年3月人均月纯收入为基数,以后每月的增长率为a,为了使该家庭2020年底能达到人均年纯收入8000元的标准,a至少为多少 (结果保留两位小数)
(参考数据:≈62.81)(参考公式:1+x+x2+…+x9=;(1+a)10≈1+10a+45a2+120a3(|a|<0.15).
20.已知直线y=x+3分别交x轴和y轴于点A和B,抛物线y=ax2+bx+c经过点A和B,且抛物线的对称轴为直线x=﹣2.
(1)抛物线与x轴的另一个交点C的坐标为 ;
(2)试确定抛物线的解析式;
(3)在同一平面直角坐标系中分别画出两个函数的图象(请用2B铅笔或黑色水笔加黑加粗),观察图象,写出二次函数值小于一次函数值的自变量x的取值范围 .
21.关于x的二次函数与x轴有交点.
(1)求a的取值范围;
(2)当时,求抛物线与x轴两个交点间的距离.
22.如图,抛物线与轴交于(-1,0),(3,0)两点,直线与抛物线交于、两点,其中点的横坐标为2.
(1)求抛物线及直线的函数表达式;
(2)点是线段上的点(不与,重合)过作轴交抛物线于,若点的横坐标为,请用含的代数式表示的长.
23.已知二次函数的图象过点
(1)此二次函数的表达式,并用配方法将其化为的形式
(2)画出此函数的图象;
(3)借助图象,判断若,则 的取值范围是
24.求下列二次函数的顶点坐标:
(1)(配方法)
(2)(公式法)
25.某数学兴趣小组对函数的图象和性质进行探究,发现自变量的取值范围是全体实数,与的几组对应值列表如下:
… 0 1 2 3 …
… 0 …
(1)补全上表;
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程有 个实数根;
②关于的方程有2个实数根时,的取值范围是 .
③当取何值时,随的增大而增大?
26.已知抛物线的顶点坐标是,且过点.
求这个抛物线对应的函数表达式.
在所给坐标系中画出该函数的图象.
当取什么值时,函数值小于0
答案
一、单选题
B.D.D.D.C.C.B.D.
二、填空题
9..
10.①③④.
11.y=(x+1)(x﹣5).(答案不唯一).
12..
13.x1=-1,x2=3.
14.①③④.
15.①③④.
16..
三、解答题
17.
解:(1)由图表可知抛物线y=ax2+bx+c过点(1,2),(3,2),
∴对称轴为x==2;
∴顶点坐标为:(2,1),
∴设y=a(x﹣2)2+1,
将(0,5)代入可得:4a+1=5,
解得:a=1,
∴二次函数的解析式为:y=(x﹣2)2+1,即y=x2﹣4x+5,
所求二次函数的关系式为y=x2﹣4x+5.
(2)描点、连线画出函数图象如图:
;
(3)∵新图象与二次函数y=ax2+bx+c的图象关于x轴对称,
∴﹣y=x2﹣4x+5,
∴新图象的函数关系式为y=﹣x2+4x﹣5,
故答案为y=﹣x2+4x﹣5.
18.
(1)∵函数图象过点,
∴将点代入y=ax2+(a+1)x,
解得:a=﹣2,
;
(2)①∵(x1,y1),(x2,y2)为此二次函数图象上两个不同点
∴x1≠x2,
∵y1=y2,
∴ax12+(a+1)x1=ax22+(a+1)x2,
∴a(x1+x2)(x1﹣x2)=(a+1)(x2﹣x1),
a(x1+x2)=﹣(a+1),
∵x1+x2=4,
∴a=;
②函数y=ax2+(a+1)x的对称轴是,
∵x1>x2≥2,对任意的x1,x2都有,
当a>0时,无法满足条件;
当a<0时,,,
∴.
19.
(1)设人均月纯收入y与月份代码x之间的函数表达式为y=kx+m,
将数据(1,310),(2,350)代入得:解得
故函数表达式为y=40x+270.
(2)2020年1月对应x=13,2020年12月对应x=24,
则2020年该家庭的人均年纯收入为12个月人均月纯收入之和,
即(13×40+270)+(14×40+270)+…+(24×40+270)=270×12+40×(13+14+…+24)=12120>8000,
故2020年底该家庭能达到人均年纯收入8000元的标准.
(3)该家庭2019年12月人均月纯收入为:12×40+270=750(元)
该家庭2020年3月份的人均月纯收入为750×=500(元);
由题意得,152+15b+c=500,∴c=275-15b,又242+24b+c≥1400,∴b≥61,
故b的最小值为61.
(4)由题意,1000+500+500(1+a)+500(1+a)2+…+500(1+a)9≥8000,
得≥7000,其中(1+a)10≈1+10a+45a2+120a3(|a|<0.15),整理得:120a2+45a-4≥0.
令120a2+45a-4=0,得a=,∴a1≈0.07,a2≈-0.45,
故不等式的解集为a≤-0.45(舍去)或a≥0.07,∴a至少应为0.07.
20.
解:(1)∵直线y=x+3分别交x轴和y轴于点A和B,
∴点A(﹣3,0),点B(0,3),
∵抛物线的对称轴为直线x=﹣2.抛物线与x轴的另一个交点为C,
∴点C(﹣1,0),
故答案为(﹣1,0);
(2)∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),点C(﹣1,0),
∴,解得:,
∴二次函数的解析式为:y=x2+4x+3;
(3)如图所示:
当﹣3<x<0时,二次函数值小于一次函数值,
故答案为:﹣3<x<0.
21.
解:(1)∵二次函数y=(a-2)x2-8x+4与x轴有交点,
∴82-4×(a-2)×4=-16a+96≥0,a-2≠0,
解得,a≤6且a≠2;
(2)当a=3时,二次函数为:y=x2-8x+4,
设抛物线与x轴两个交点的坐标为(x1,0)、(x2,0),
则x1+x2=8,x1 x2=4,
.
22.
解:(1)把A(-1,0)、B(3,0)代入y=x2+bx-c得:
,
解得:,
∴解析式为:y=x2-2x-3,
把x=2代入y=x2-2x-3得y=-3,
∴C(2,-3),
设直线AC的解析式为y=kx+n,
把A(-1,0)、C(2,-3)代入得,
解得:,
∴直线AC的解析式为;
(2)∵点M在直线AC上,
∴M的坐标为(m,-m-1);
∵点F在抛物线y=x2-2x-3上,
∴F点的坐标为(m,m2-2m-3),
∴MF=(-m-1)-( m2-2m-3)=-m2+m+2.
23.
(1)把代入,
得,
解得:,
∴二次函数的表达式为:,
配方得:
(2)∵,
∴顶点坐标为(1,4),对称轴方程为x=1,
当y=0时,,
,
∴图像与x轴的交点坐标为(-1,0)(3,0),
又∵图像过点
可得下图:
(3)由图可得当时,则 的取值范围是,
故答案为:.
24.
解:(1)
,
∴顶点坐标为(2,-4)
(2),
∵,,,
∴,,
∴顶点坐标为顶点坐标为.
25.
解:(1)如下表:
(2)如图,
(3)①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当-2≤x≤0或x≥2时,y随x的增大而增大.
26.
解:(1)∵抛物线的顶点坐标是,
设抛物线的解析式为,
抛物线过点,
,
,
抛物线的解析式为;
(2)列表:
x … -3 -2 -1 0 1 …
y … 0 3 4 3 0 …
描点:在平面直角坐标系中描出点(-3,0),(-2,3),(-1,4),(0,3),(1,0)
连线:用平滑曲线连接,
(3)∵函数值小于,
∴函数图像再x轴下方,在-3左侧和1右侧,
当x<-3或x>1时,函数值小于.
同课章节目录
