九年级数学上册试题 1.4二次函数的应用习题-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 1.4二次函数的应用习题-浙教版(含答案) |

|
|
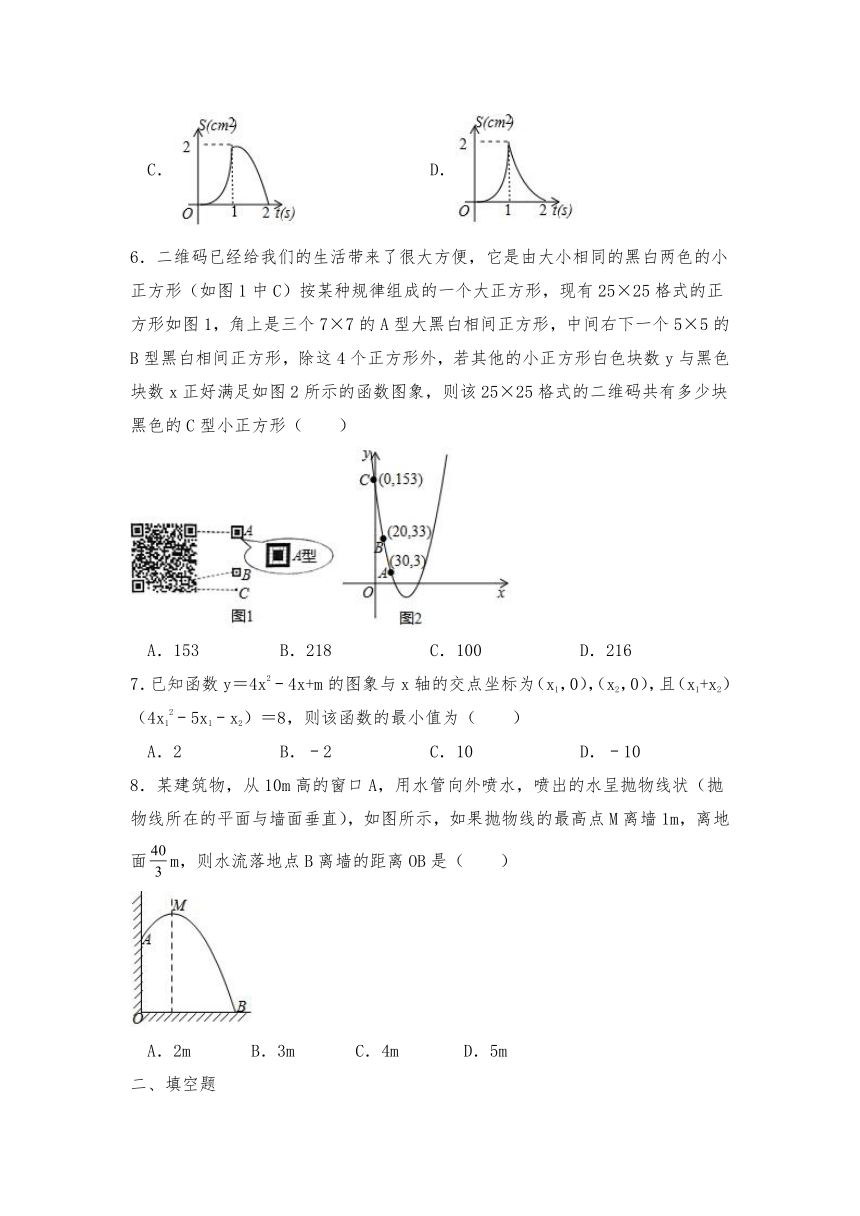
| 格式 | docx | ||
| 文件大小 | 720.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 22:45:55 | ||
图片预览




文档简介
1.4二次函数的应用
一、单选题
1.如图,抛物线与轴交于点,其对称轴为直线,结合图象分析下列结论:①;②;③当时,随的增大而增大;④一元二次方程的两根分别为,;⑤;⑥若,为方程的两个根,则且,其中正确的结论有( )
A.个 B.个 C.个 D.个
2.如图,在正方形ABCD中,边长CD为3cm.动点P从点A出B发,以cm/s的速度沿AC方向运动到点C停止. 动点Q同时从点A出发,以1cm/s的速度沿折线AB→BC方向运动到点C停止.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A.B.
C.D.
3.如图,已知抛物线与直线交于,两点,则关于的不等式的解集是( )
A.或 B.或 C. D.
4.汽车刹车后行驶的距离s(单位:米)与行驶的时间t(单位:秒)的函数关系式是s=15t-6t2,那么汽车刹车后几秒停下来?( )
A.0 B.1.25 C.2.5 D.3
5.如图,正方形的边长为,点,点同时从点出发,速度均,点沿向点运动,点沿向点运动,则的面积与运动时间之间函数关系的大致图象是( )
A. B.
C. D.
6.二维码已经给我们的生活带来了很大方便,它是由大小相同的黑白两色的小正方形(如图1中C)按某种规律组成的一个大正方形,现有25×25格式的正方形如图1,角上是三个7×7的A型大黑白相间正方形,中间右下一个5×5的B型黑白相间正方形,除这4个正方形外,若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象,则该25×25格式的二维码共有多少块黑色的C型小正方形( )
A.153 B.218 C.100 D.216
7.已知函数y=4x2﹣4x+m的图象与x轴的交点坐标为(x1,0),(x2,0),且(x1+x2)(4x12﹣5x1﹣x2)=8,则该函数的最小值为( )
A.2 B.﹣2 C.10 D.﹣10
8.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
二、填空题
9.用一根长为的铁丝,把它折成一个长方形框.设长方形的宽为,面积为,则关于的函数关系式是________.
10.如图,在平面直角坐标系中,O为坐标原点,点A(-3,0)在抛物线上,点B是该抛物线与y轴的交点,过点B作轴交抛物线于点C,连结AB,AC.若AC平分∠BAO.则此抛物线对应的函数解析式为__________.
11.如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.
12.今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
(1)小华的问题解答: ;
(2)小明的问题解答: .
13.如图,抛物线y=x2+bx-3与x轴交于A、B两点(点A在点B左侧),直线l与抛物线交于A、C两点,其中点A、C的横坐标分别为-1和2.点G是抛物线上的动点,在x轴上存在点F,使以A、C、F、G四个点为顶点的四边形是平行四边形,则点F的坐标为________.
14.二次函数y=ax2+bx+c(a≠0)的图象如图所示,请直接写出不等式ax2+bx+c>0的解集_____.
15.如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点A,点M是抛物线x轴上方任意一点,过点M作MP⊥x轴于点P,以MP为对角线作矩形MNPQ,连结NQ,则对角线NQ的取值范围为_________.
16.把一根长30cm的铁丝分为两部分,每一部分均弯曲成一个正三角形,它们的面积和的最小值是_____cm2.
三、解答题
17.某学习小组在研究函数的图象与性质时,已列表、描点并画出了图象的一部分.
x 0 1 2 3 4
y 0
(1)请补全函数图象;
(2)方程实数根的个数为______;其中一根为______.
(3)观察图象,写出该函数y随x增大而增大时,自变量x的取值范围.
18.如图,有一块三角形土地,它的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面积是矩形DEFG的大楼.
(1)求地基的面积y(m2)和边EF的长x(m)的函数关系式;
(2)当地基的边长EF为多少时地基的面积最大,最大面积是多少?
19.劳动是财富的源泉,也是幸福的源泉.沈河区某中学对劳动教育进行积极探索和实践,创建学生劳动教育基地,让学生参与农耕劳作.如图,现计划利用校园围墙的一段MN(MN最长可用25m),用40m长的篱笆,围成一个长方形菜园ABCD.设AB的长为xm(7.2≤x>20).
(1)BC的长度为 m(用含x的代数式表示),长方形菜园的面积S(m2)与AB的长x(m)的关系式为S= ;
(2)根据(1)中的关系式完成如表:
AB的长x(m) 8 9 10 11 12 13 14 15 ……
菜园的面积S(m2) 192 198 182 168 150 ……
(3)请根据表中数据分析,S如何随x的变化而变化?(写出一个结论即可)
20.如图1,在平面直角坐标系中,抛物线与直线交于点和点,与轴交于点.
(1)求,的值及抛物线的解析式;
(2)在图1中,把向上平移个单位长度,始终保持点的对应点在第二象限抛物线上,点,的对应点分别为,,若直线与的边有两个交点,求的取值范围;
(3)如图2,在抛物线上是否存在点(不与点重合),使和的面积相等?若存在,直接写出点的坐标;若不存在,请说明理由.
21.端午节前夕,某超市调研一种进价为4元/个的粽子的销售情况,当每个售价为6元时,每天能卖出1400个,在此基础上售价每上涨0.1元,每天销售量将减少10个.根据物价局规定,售价不能超过进价的300%.
(1)若要实现每天6000元的销售利润,售价应定为多少?
(2)若按照物价局规定的最高售价,每天的利润会超过6000元吗?请说明理由.
22.如图,抛物线经过点,顶点,对称轴交轴于点,
(1)求抛物线的解析式;
(2)在第一象限内的抛物线上求点,使得是以为底边的等腰三角形,求出此时点的坐标;
(3)在(2)的基础上,点是否是第一象限内的抛物线上与距离最远的点?若是,请说明理由;若不是,请求出第一象限内的抛物线上与距离最远的点的坐标.
23.某商家采取线上和线下两种方式销售某款商品,规定无论是线上还是线下每件售价不低于进价,且线上售价始终比线下每件便宜元.已知该款商品进价为元/件,线上的月销售量固定为件,线下的月销售量(件)与线下售价(元/件)满足关系式.设该商品线上和线下月销售利润总和为(元).
(1)求与之间的函数关系式(不要求写出自变量的取值范围);
(2)若该商家每月想从这种商品销售中获得元的利润,又想尽量给客户实惠,该如何给这种商品进行线下定价?
(3)物价部门规定,该商品的每件利润不得高于进价的,如果商家每月要想从这种商品销售中获得最大利润,他应该把这种商品的线下售价定为多少?月最大销售利润是多少?
24.如图,在边长为120cm的正方形铁皮ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体工艺盒(A,B,C,D四个顶点正好重合于上底面一点).已知点M,N在CD边上,且是被剪去的一个等腰直角三角形斜边的两个端点,设CM=DN=x(cm).
(1)若折成的包装盒恰好是个正方体,求这个工艺盒的体积;
(2)当x取何值时,工艺盒的四个侧面面积和S最大,最大值为多少?
25.某超市销售一种除菌液,进货价为每瓶5元,规定每瓶的售价不能低于进货价,每瓶的利润不能高于进货价.经市场调查,每天的销售量(瓶)与每瓶的售价(元)满足一次函数关系,部分数据如下表:
售价(元/瓶) 5 6 7
销售量(瓶) 160 140 120
(1)求出与之间的函数关系式;(不需要求自变量的取值范围)
(2)设超市销售该品牌除菌液每天的销售利润为元,当每瓶除菌液的售价定为多少元时,超市销售该品牌除菌液每天的销售利润最大,最大利润是多少元?
26.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米.
(1)求出y和x的函数关系式,并写出x的取值范围;
(2)求y的最大值.
答案
一、单选题
C.D.D.B.C.C.D.B.
二、填空题
9.y=-x2+50x
10..
11.5.
12.当定价为4元时,能实现每天800元的销售利润.
800元的销售利润不是最多,当定价为4.8元时,每天的销售利润最大.
13.(1,0)、(-3,0)、、.
14.1<x<3.
15.0<NQ<4.
16..
三、解答题
17.
解:(1)如图,
(2)根据图像可知:方程2x=0有3个实数根;其中一根为x=0;
故答案为3,0;
(3)当x<﹣2或x>2时,函数y随x增大而增大.
18.
解:(1)∵四边形DEFG为矩形,
∴EF=DG=x,DG∥BC,
∵DE⊥BC,
∴DE=HM,
∵DG∥BC,
∴△ADG∽△ABC,
∴,
∴,
∴AM=x,
∴DE=80﹣x,
∴y=DE×DG==80x﹣;
(2)∵y=﹣+80x=﹣(x﹣50)2+2000,
∴当x=50时,y的最大值为2000,
即当EF=50m时,地基的面积最大,最大面积为2000m2.
19.
解:(1)BC=40﹣AB﹣CD=(40﹣2x)m,
S=AB BC=x(40﹣2x)=﹣2x2+40x,
故答案为:(40﹣2x),﹣2x2+40x.
(2)将x=9,10,12分别代入解析式可得S=198,200,192.
故答案为:198,200,192.
(3)当x<10时,S随x增大而增大.
20.
(1)∵点、在直线上,
∴,.
∴,.
∴、.
又∵、在抛物线上,
∴,解得,.
∴抛物线的解析式为.
(2)如图,当点移动到上时,是△PMN与直线AB有唯一公共点M的终止临界位置,
过点B作BR⊥x轴于点R,则
∴AR=BR.
∴△ABR是等腰直角三角形,∠BAR=∠ABR=45°.
∵OA=OC=3,
∴△ACO是等腰直角三角形,∠CAO=45°,且
过点 P作PH⊥x 轴,交 AB于点 H,则∠PHM=∠HBR=45°.
由平移的性质可知,PM∥AC且PM=AC.
∴∠PMH=∠BAC=90°,
∴是等腰直角三角形,且
令,则,
∴,解得,(不合题意,舍去).
当t=-4时,
∴,此时.
∵初始位置时,△ACO的边与直线AB有唯一公共点 A,
∴符合条件的m的取值范围是.
(3)存在.点的坐标为(-1,-4)或(3,12)或(-4,5).
分两种情况:
①当点在直线的下方时,过点作的平行线与抛物线的交点即为满足题意的点,如图2所示,
∵,可设直线的解析式为.将代入,得,
∴直线的解析式为.联立直线和抛物线的解析式,
解得,或(舍去).
故点的坐标为(-1,-4).
②当点在直线的上方时,设.
过点作于点,如图所示,则.
∵和的面积相等,
∴
∴四边形为平行四边形.
∴线段的中点在直线上,
则,
解得,或-4,故点的坐标为(3,12)或(-4,5).
综上所述,符合条件的点的坐标为(-1,-4)或(3,12)或(-4,5).
21.
解:(1)设售价为元,由题意得:
解得或,
售价不能超过进价的.
,即,
,
答:若要实现每天6000元的销售利润,售价应定为10元.
(2)设售价为元,利润为元,由题意得
,
当时,函数能取得最大值,最大值为6400元.
答:按照物价局规定的最高售价,每天的利润会超过6000元,最大利润是6400元.
22.
解:(1)∵抛物线 的顶点坐标是B(1,2),
∴ ,
∵抛物线经过点A(0,1),
∴ ,
解得:a=-1,
所以抛物线的解析式为或;
(2)∵A(0,1),C(1,0),
∴OA=OC,
若PA=PC,
则点P在直线上,
即直线与抛物线在第一象限的交点即为点P.
令=,
解得:=(舍)或,
∴P点的坐标为;
(3)假设Q点是第一象限内的抛物线上与AC距离最远的点,
则△AQC的面积最大,即四边形OAQC的面积最大,连接OQ,
=
当时,四边形OAQC的面积最大,
此时点Q的坐标为 .
23.
解:根据题意,则
(1);
(2)依题意得:
,
解得:,
∵想尽量给客户实惠,
这种商品线下售价为元/件.
根据题意得.
由知,
在内,随的增大而增大
时,的最大值为(元).
要想获得最大利润,线下售价应为元/件,月最大利润为元.
24.
解:(1)根据题意,设CM=DN=x(cm),折成的工艺盒恰好是个正方体,
由勾股定理可得:MG=GN=x,MN=2x
∵正方形纸片ABCD边长为120cm,即CM+MN+DN=120
∴x+2x+x=120,解得:x=30,
∴正方体的底面边长a=30,
∴V=a3==5400(cm3);
答:这个工艺盒的体积是5400cm3;
(2)设工艺盒的底面边长为acm,高为hcm,
则a=x,h==(60﹣x),
∴S=4ah=4x (60﹣x)=﹣8x2+480x=﹣8(x﹣30)2+7200,
∵0<x<60,
∴当x=30时,S最大,最大值为7200cm2.
25.
解:(1)∵与满足一次函数关系,
∴设与之间的函数关系式为.
将,;,代入,
得,解得,
∴与之间的函数关系式为:;
(2).
∵,
∴抛物线开口向下,有最大值,
根据每瓶的售价不能低于进货价,每瓶的利润不能高于进货价,得,
∴当时,最大值为320.
答:该产品销售价定为每瓶9元时,每天销售利润最大,最大销售利润320元.
26.
解:(1)由题意可得,y=x(30-2x)=-2x2+30x,
即y与x的函数关系式是y=-2x2+30x;
∵墙的长度为18,
∴0<30-2x≤18,
解得,6≤x<15,
即x的取值范围是6≤x<15;
(2)由(1)知,y=-2x2+30x=-2,
而6≤x<15,
∴当x=7.5时,y取得最大值,此时y=112.5,
即当x=7.5米时,y的最大值是112.5平方米.
一、单选题
1.如图,抛物线与轴交于点,其对称轴为直线,结合图象分析下列结论:①;②;③当时,随的增大而增大;④一元二次方程的两根分别为,;⑤;⑥若,为方程的两个根,则且,其中正确的结论有( )
A.个 B.个 C.个 D.个
2.如图,在正方形ABCD中,边长CD为3cm.动点P从点A出B发,以cm/s的速度沿AC方向运动到点C停止. 动点Q同时从点A出发,以1cm/s的速度沿折线AB→BC方向运动到点C停止.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A.B.
C.D.
3.如图,已知抛物线与直线交于,两点,则关于的不等式的解集是( )
A.或 B.或 C. D.
4.汽车刹车后行驶的距离s(单位:米)与行驶的时间t(单位:秒)的函数关系式是s=15t-6t2,那么汽车刹车后几秒停下来?( )
A.0 B.1.25 C.2.5 D.3
5.如图,正方形的边长为,点,点同时从点出发,速度均,点沿向点运动,点沿向点运动,则的面积与运动时间之间函数关系的大致图象是( )
A. B.
C. D.
6.二维码已经给我们的生活带来了很大方便,它是由大小相同的黑白两色的小正方形(如图1中C)按某种规律组成的一个大正方形,现有25×25格式的正方形如图1,角上是三个7×7的A型大黑白相间正方形,中间右下一个5×5的B型黑白相间正方形,除这4个正方形外,若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象,则该25×25格式的二维码共有多少块黑色的C型小正方形( )
A.153 B.218 C.100 D.216
7.已知函数y=4x2﹣4x+m的图象与x轴的交点坐标为(x1,0),(x2,0),且(x1+x2)(4x12﹣5x1﹣x2)=8,则该函数的最小值为( )
A.2 B.﹣2 C.10 D.﹣10
8.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
二、填空题
9.用一根长为的铁丝,把它折成一个长方形框.设长方形的宽为,面积为,则关于的函数关系式是________.
10.如图,在平面直角坐标系中,O为坐标原点,点A(-3,0)在抛物线上,点B是该抛物线与y轴的交点,过点B作轴交抛物线于点C,连结AB,AC.若AC平分∠BAO.则此抛物线对应的函数解析式为__________.
11.如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.
12.今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
(1)小华的问题解答: ;
(2)小明的问题解答: .
13.如图,抛物线y=x2+bx-3与x轴交于A、B两点(点A在点B左侧),直线l与抛物线交于A、C两点,其中点A、C的横坐标分别为-1和2.点G是抛物线上的动点,在x轴上存在点F,使以A、C、F、G四个点为顶点的四边形是平行四边形,则点F的坐标为________.
14.二次函数y=ax2+bx+c(a≠0)的图象如图所示,请直接写出不等式ax2+bx+c>0的解集_____.
15.如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点A,点M是抛物线x轴上方任意一点,过点M作MP⊥x轴于点P,以MP为对角线作矩形MNPQ,连结NQ,则对角线NQ的取值范围为_________.
16.把一根长30cm的铁丝分为两部分,每一部分均弯曲成一个正三角形,它们的面积和的最小值是_____cm2.
三、解答题
17.某学习小组在研究函数的图象与性质时,已列表、描点并画出了图象的一部分.
x 0 1 2 3 4
y 0
(1)请补全函数图象;
(2)方程实数根的个数为______;其中一根为______.
(3)观察图象,写出该函数y随x增大而增大时,自变量x的取值范围.
18.如图,有一块三角形土地,它的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面积是矩形DEFG的大楼.
(1)求地基的面积y(m2)和边EF的长x(m)的函数关系式;
(2)当地基的边长EF为多少时地基的面积最大,最大面积是多少?
19.劳动是财富的源泉,也是幸福的源泉.沈河区某中学对劳动教育进行积极探索和实践,创建学生劳动教育基地,让学生参与农耕劳作.如图,现计划利用校园围墙的一段MN(MN最长可用25m),用40m长的篱笆,围成一个长方形菜园ABCD.设AB的长为xm(7.2≤x>20).
(1)BC的长度为 m(用含x的代数式表示),长方形菜园的面积S(m2)与AB的长x(m)的关系式为S= ;
(2)根据(1)中的关系式完成如表:
AB的长x(m) 8 9 10 11 12 13 14 15 ……
菜园的面积S(m2) 192 198 182 168 150 ……
(3)请根据表中数据分析,S如何随x的变化而变化?(写出一个结论即可)
20.如图1,在平面直角坐标系中,抛物线与直线交于点和点,与轴交于点.
(1)求,的值及抛物线的解析式;
(2)在图1中,把向上平移个单位长度,始终保持点的对应点在第二象限抛物线上,点,的对应点分别为,,若直线与的边有两个交点,求的取值范围;
(3)如图2,在抛物线上是否存在点(不与点重合),使和的面积相等?若存在,直接写出点的坐标;若不存在,请说明理由.
21.端午节前夕,某超市调研一种进价为4元/个的粽子的销售情况,当每个售价为6元时,每天能卖出1400个,在此基础上售价每上涨0.1元,每天销售量将减少10个.根据物价局规定,售价不能超过进价的300%.
(1)若要实现每天6000元的销售利润,售价应定为多少?
(2)若按照物价局规定的最高售价,每天的利润会超过6000元吗?请说明理由.
22.如图,抛物线经过点,顶点,对称轴交轴于点,
(1)求抛物线的解析式;
(2)在第一象限内的抛物线上求点,使得是以为底边的等腰三角形,求出此时点的坐标;
(3)在(2)的基础上,点是否是第一象限内的抛物线上与距离最远的点?若是,请说明理由;若不是,请求出第一象限内的抛物线上与距离最远的点的坐标.
23.某商家采取线上和线下两种方式销售某款商品,规定无论是线上还是线下每件售价不低于进价,且线上售价始终比线下每件便宜元.已知该款商品进价为元/件,线上的月销售量固定为件,线下的月销售量(件)与线下售价(元/件)满足关系式.设该商品线上和线下月销售利润总和为(元).
(1)求与之间的函数关系式(不要求写出自变量的取值范围);
(2)若该商家每月想从这种商品销售中获得元的利润,又想尽量给客户实惠,该如何给这种商品进行线下定价?
(3)物价部门规定,该商品的每件利润不得高于进价的,如果商家每月要想从这种商品销售中获得最大利润,他应该把这种商品的线下售价定为多少?月最大销售利润是多少?
24.如图,在边长为120cm的正方形铁皮ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体工艺盒(A,B,C,D四个顶点正好重合于上底面一点).已知点M,N在CD边上,且是被剪去的一个等腰直角三角形斜边的两个端点,设CM=DN=x(cm).
(1)若折成的包装盒恰好是个正方体,求这个工艺盒的体积;
(2)当x取何值时,工艺盒的四个侧面面积和S最大,最大值为多少?
25.某超市销售一种除菌液,进货价为每瓶5元,规定每瓶的售价不能低于进货价,每瓶的利润不能高于进货价.经市场调查,每天的销售量(瓶)与每瓶的售价(元)满足一次函数关系,部分数据如下表:
售价(元/瓶) 5 6 7
销售量(瓶) 160 140 120
(1)求出与之间的函数关系式;(不需要求自变量的取值范围)
(2)设超市销售该品牌除菌液每天的销售利润为元,当每瓶除菌液的售价定为多少元时,超市销售该品牌除菌液每天的销售利润最大,最大利润是多少元?
26.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米.
(1)求出y和x的函数关系式,并写出x的取值范围;
(2)求y的最大值.
答案
一、单选题
C.D.D.B.C.C.D.B.
二、填空题
9.y=-x2+50x
10..
11.5.
12.当定价为4元时,能实现每天800元的销售利润.
800元的销售利润不是最多,当定价为4.8元时,每天的销售利润最大.
13.(1,0)、(-3,0)、、.
14.1<x<3.
15.0<NQ<4.
16..
三、解答题
17.
解:(1)如图,
(2)根据图像可知:方程2x=0有3个实数根;其中一根为x=0;
故答案为3,0;
(3)当x<﹣2或x>2时,函数y随x增大而增大.
18.
解:(1)∵四边形DEFG为矩形,
∴EF=DG=x,DG∥BC,
∵DE⊥BC,
∴DE=HM,
∵DG∥BC,
∴△ADG∽△ABC,
∴,
∴,
∴AM=x,
∴DE=80﹣x,
∴y=DE×DG==80x﹣;
(2)∵y=﹣+80x=﹣(x﹣50)2+2000,
∴当x=50时,y的最大值为2000,
即当EF=50m时,地基的面积最大,最大面积为2000m2.
19.
解:(1)BC=40﹣AB﹣CD=(40﹣2x)m,
S=AB BC=x(40﹣2x)=﹣2x2+40x,
故答案为:(40﹣2x),﹣2x2+40x.
(2)将x=9,10,12分别代入解析式可得S=198,200,192.
故答案为:198,200,192.
(3)当x<10时,S随x增大而增大.
20.
(1)∵点、在直线上,
∴,.
∴,.
∴、.
又∵、在抛物线上,
∴,解得,.
∴抛物线的解析式为.
(2)如图,当点移动到上时,是△PMN与直线AB有唯一公共点M的终止临界位置,
过点B作BR⊥x轴于点R,则
∴AR=BR.
∴△ABR是等腰直角三角形,∠BAR=∠ABR=45°.
∵OA=OC=3,
∴△ACO是等腰直角三角形,∠CAO=45°,且
过点 P作PH⊥x 轴,交 AB于点 H,则∠PHM=∠HBR=45°.
由平移的性质可知,PM∥AC且PM=AC.
∴∠PMH=∠BAC=90°,
∴是等腰直角三角形,且
令,则,
∴,解得,(不合题意,舍去).
当t=-4时,
∴,此时.
∵初始位置时,△ACO的边与直线AB有唯一公共点 A,
∴符合条件的m的取值范围是.
(3)存在.点的坐标为(-1,-4)或(3,12)或(-4,5).
分两种情况:
①当点在直线的下方时,过点作的平行线与抛物线的交点即为满足题意的点,如图2所示,
∵,可设直线的解析式为.将代入,得,
∴直线的解析式为.联立直线和抛物线的解析式,
解得,或(舍去).
故点的坐标为(-1,-4).
②当点在直线的上方时,设.
过点作于点,如图所示,则.
∵和的面积相等,
∴
∴四边形为平行四边形.
∴线段的中点在直线上,
则,
解得,或-4,故点的坐标为(3,12)或(-4,5).
综上所述,符合条件的点的坐标为(-1,-4)或(3,12)或(-4,5).
21.
解:(1)设售价为元,由题意得:
解得或,
售价不能超过进价的.
,即,
,
答:若要实现每天6000元的销售利润,售价应定为10元.
(2)设售价为元,利润为元,由题意得
,
当时,函数能取得最大值,最大值为6400元.
答:按照物价局规定的最高售价,每天的利润会超过6000元,最大利润是6400元.
22.
解:(1)∵抛物线 的顶点坐标是B(1,2),
∴ ,
∵抛物线经过点A(0,1),
∴ ,
解得:a=-1,
所以抛物线的解析式为或;
(2)∵A(0,1),C(1,0),
∴OA=OC,
若PA=PC,
则点P在直线上,
即直线与抛物线在第一象限的交点即为点P.
令=,
解得:=(舍)或,
∴P点的坐标为;
(3)假设Q点是第一象限内的抛物线上与AC距离最远的点,
则△AQC的面积最大,即四边形OAQC的面积最大,连接OQ,
=
当时,四边形OAQC的面积最大,
此时点Q的坐标为 .
23.
解:根据题意,则
(1);
(2)依题意得:
,
解得:,
∵想尽量给客户实惠,
这种商品线下售价为元/件.
根据题意得.
由知,
在内,随的增大而增大
时,的最大值为(元).
要想获得最大利润,线下售价应为元/件,月最大利润为元.
24.
解:(1)根据题意,设CM=DN=x(cm),折成的工艺盒恰好是个正方体,
由勾股定理可得:MG=GN=x,MN=2x
∵正方形纸片ABCD边长为120cm,即CM+MN+DN=120
∴x+2x+x=120,解得:x=30,
∴正方体的底面边长a=30,
∴V=a3==5400(cm3);
答:这个工艺盒的体积是5400cm3;
(2)设工艺盒的底面边长为acm,高为hcm,
则a=x,h==(60﹣x),
∴S=4ah=4x (60﹣x)=﹣8x2+480x=﹣8(x﹣30)2+7200,
∵0<x<60,
∴当x=30时,S最大,最大值为7200cm2.
25.
解:(1)∵与满足一次函数关系,
∴设与之间的函数关系式为.
将,;,代入,
得,解得,
∴与之间的函数关系式为:;
(2).
∵,
∴抛物线开口向下,有最大值,
根据每瓶的售价不能低于进货价,每瓶的利润不能高于进货价,得,
∴当时,最大值为320.
答:该产品销售价定为每瓶9元时,每天销售利润最大,最大销售利润320元.
26.
解:(1)由题意可得,y=x(30-2x)=-2x2+30x,
即y与x的函数关系式是y=-2x2+30x;
∵墙的长度为18,
∴0<30-2x≤18,
解得,6≤x<15,
即x的取值范围是6≤x<15;
(2)由(1)知,y=-2x2+30x=-2,
而6≤x<15,
∴当x=7.5时,y取得最大值,此时y=112.5,
即当x=7.5米时,y的最大值是112.5平方米.
同课章节目录
