九年级数学上册试题 3.1 圆同步练习-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 3.1 圆同步练习-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 309.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 22:51:27 | ||
图片预览



文档简介
3.1 圆
一、单选题
1.已知的半径为,圆心到直线的距离为,则直线与的位置关系为 ( )
A.相交 B.相切 C.相离 D.无法确定
2.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm B.6cm C.7cm D.8cm
3.已知的半径为,点与圆心的距离为,则点与的位置关系是( )
A.点在内 B.点在上
C.点在外 D.点不在内
4.下列说法错误的是( )
A.圆上的点到圆心的距离相等 B.过圆心的线段是直径
C.直径是圆中最长的弦 D.半径相等的圆是等圆
5.点在半径为的外,则点到圆心的距离与的关系是( )
A. B. C. D.
6.已知在中,半径,弦,则的值不可以是( )
A.6 B.8
C.10 D.12
7.下列说法中,不正确的是( )
A.圆既是轴对称图形又是旋转对称图形
B.一个圆的直径的长是它半径的2倍
C.圆的每一条直径都是它的对称轴
D.直径是圆的弦,但半径不是弦
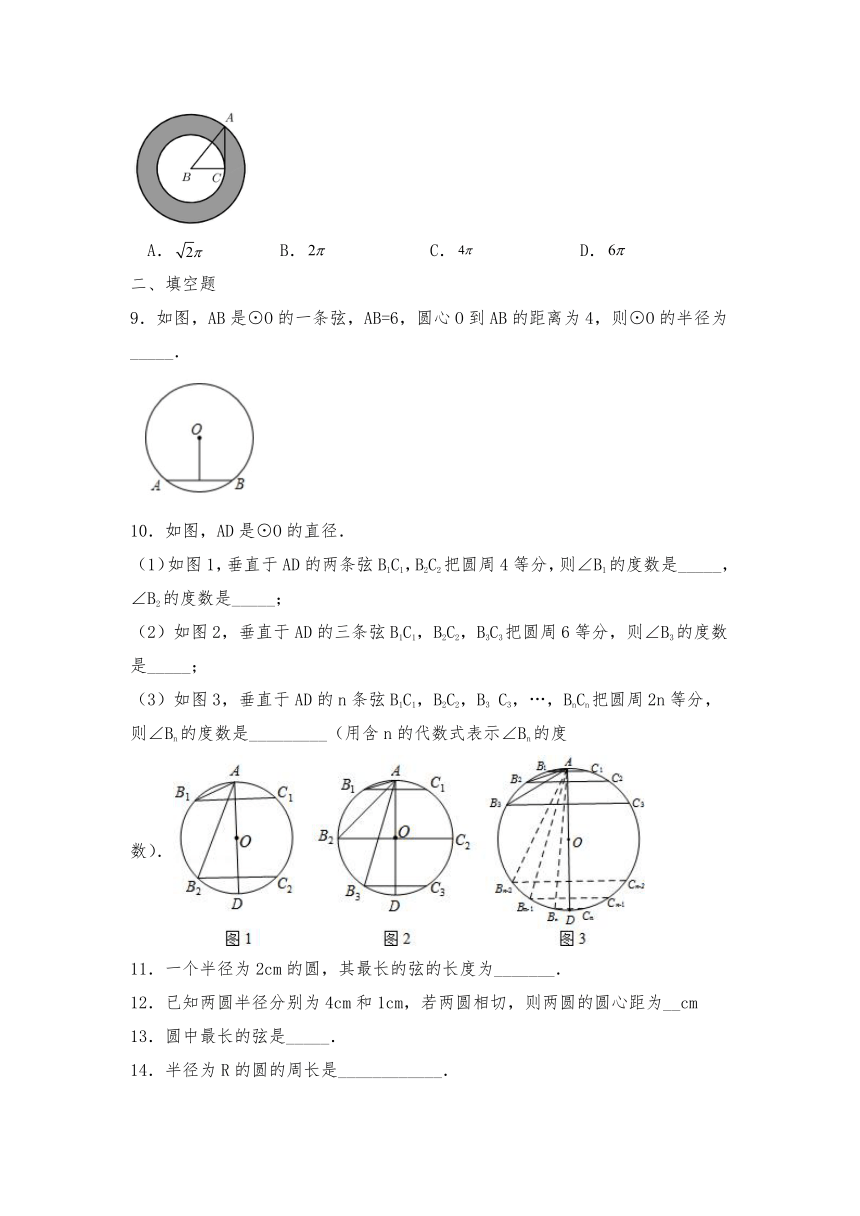
8.如图,在直角中,,则以为圆心,分别为半径的圆形成一个圆环,则该圆环的面积为( ).
A. B. C. D.
二、填空题
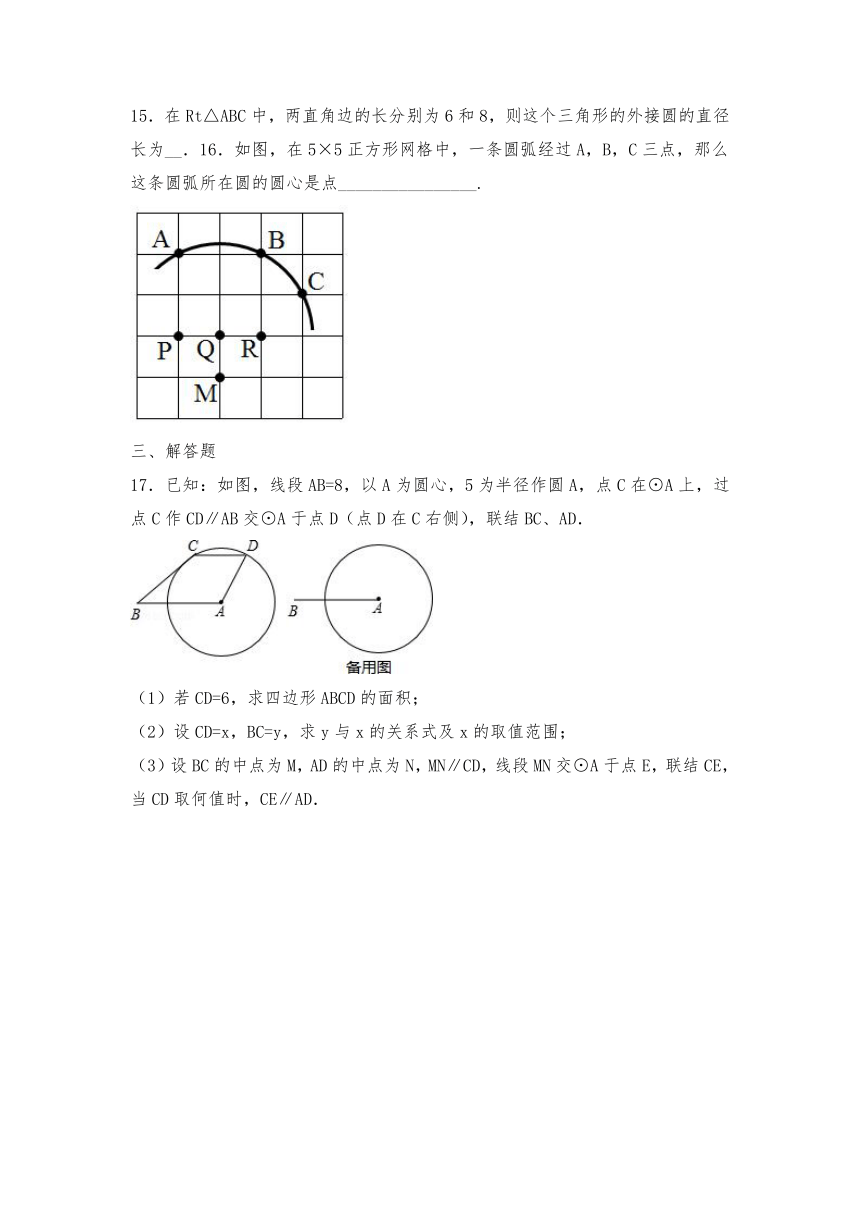
9.如图,AB是⊙O的一条弦,AB=6,圆心O到AB的距离为4,则⊙O的半径为_____.
10.如图,AD是⊙O的直径.
(1)如图1,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是_____,∠B2的度数是_____;
(2)如图2,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,则∠B3的度数是_____;
(3)如图3,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,则∠Bn的度数是_________(用含n的代数式表示∠Bn的度数).
11.一个半径为2cm的圆,其最长的弦的长度为_______.
12.已知两圆半径分别为4cm和1cm,若两圆相切,则两圆的圆心距为__cm
13.圆中最长的弦是_____.
14.半径为R的圆的周长是____________.
15.在Rt△ABC中,两直角边的长分别为6和8,则这个三角形的外接圆的直径长为__.16.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是点________________.
三、解答题
17.已知:如图,线段AB=8,以A为圆心,5为半径作圆A,点C在⊙A上,过点C作CD∥AB交⊙A于点D(点D在C右侧),联结BC、AD.
(1)若CD=6,求四边形ABCD的面积;
(2)设CD=x,BC=y,求y与x的关系式及x的取值范围;
(3)设BC的中点为M,AD的中点为N,MN∥CD,线段MN交⊙A于点E,联结CE,当CD取何值时,CE∥AD.
18.已知点P、Q,且PQ=4cm,
(1)画出下列图形:到点P的距离等于2cm的点的集合;到点Q的距离等于3cm的点的集合.
(2)在所画图中,到点P的距离等于2cm,且到点Q的距离等于3cm的点有几个?请在图中将它们表示出来.
19.已知:如图,在中,是直径,为不是直径的弦,求证:是中最长的弦.
20.如图,在△ABC中,∠ACB=90°,∠A=40°;以C为圆心、CB为半径的圆交AB于点D,求∠ACD的度数.
21.如图所示,在四边形ABCD ,∠B=∠D=90°,求证:A、B、C、D四点在同一个圆上.
22.如图,AB、AC是⊙O的两条弦,且AB=AC.求证:∠1=∠2.
23.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线相交于点E.已知AB=2DE,∠E=18°.试求∠AOC的度数.
24.以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,若BC=12,CD=5.求⊙A的半径r的取值范围.
25.已知两点A、B和直线l,求作一圆,使之经过A、B两点,且圆心在直线l上.
26.如图,CD是的直径,点A在DC的延长线上,AE交于点B,AB等于的半径,,求的度数.
答案
一、单选题
B.A.A.B.D.D.C.B.
二、填空题
9.5.
10.22.5° 67.5° 75°
11.4cm.
12.5或3.
13.直径.
14.2πR.
15.10.
16.Q.
三、解答题
17.(1)作AH⊥CD于H,如图,
则CH=DH=CD=×6=3,
在Rt△AHD中,∵AD=5,DH=3,
∴AH==4,
∴四边形ABCD的面积=(CD+AB) AH=×(6+8)×4=28;
(2)作CP⊥AB于P,如图1,
∵AH⊥CD,CD=x
∴CH=DH=x,
∴AP=CH=x,
∴BP=AB-AP=8-x,
在Rt△PAC中,∵AC2=AP2+CP2,
∴CP2=25-x2,
在Rt△BPC中,∵BC2=BP2+CP2,
∴y2=(8-x)2+25-x2=89-8x,
∴y=(0<x<10);
(3)设AH交MN于点F,连结AE,如图2,
∵CD∥AB,CD≠AB,
∴四边形ABCD为梯形,
∵BC的中点为M,AD的中点为N,
∴MN为梯形ABCD的中位线,
∴MN∥CD,
∵CE∥AD,
∴四边形CEND为平行四边形,
∴DC=NE=x,
∵FN∥CD,N点为AD的中点,
∴FN为△AHD的中位线,
∴FN=DH=x,
∴EF=x-x=x,
在Rt△AEF中,AF2=AE2-EF2,
在Rt△AFN中,AF2=AN2-NF2,
∴AE2-EF2=AN2-NF2,即52-(x)2=()2-(x)2,解得x=.
即当CD为时,CE∥AD.
18.
解:(1)到点P的距离等于2cm的点的集合图中⊙P;到点Q的距离等于3cm的点的集合图中⊙Q.
(2)到点P的距离等于2cm,且到点Q的距离等于3cm的点有2个,图中C、D.
19.
证明:如图,连接,,
、、、是圆的半径,
.
是圆的直径,
.
、、是三角形的三边,
.
即.
是中最长的弦.
20.
解:连接CD,∵∠ACB=90°,∠A=40°,
∴∠B=50°,
∵CD=CB,
∴∠BCD=180°-2×50°=80°,
∴∠ACD=90°-80°=10°.
故答案为10°.
21.
证明:连AC,取AC的中点O,连接OB、OD,
∵∠B=∠D=90°,
∴OB=AC,OD=AC.即OB=OA=OC=OD,
∴ A、B、C、D四点在同一圆上.
22.
连接OB、OC.
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS).
∴∠1=∠2.
23.
连接OD,
∵AB=2DE,AB=2OD,
∴OD=DE,∴∠DOE=∠E,
∴∠ODC=2∠E=36°,
∵OC=OD,∴∠C=∠ODC=36°,
∴∠AOC=∠C+∠E=54°
24.
解:根据题意画出图形如下所示:
∵AB=CD=5,AD=BC=12,
根据矩形的性质和勾股定理得到:AC==13.
∵AB=5,AD=12,AC=13,
而A,C,D中至少有一个点在⊙A内,且至少有一个点在⊙A外,
∴点B在⊙A内,点C在⊙A外.
∴5<r<13.
故答案为:5<r<13.
25.
解:连接AB,作线段AB的垂直平分线交直线于点O.以点O为圆心,AO为半径作圆,
则⊙O即为所求,
26.
解:∵AB等于的半径,
∴,
∴
∵
∴
∵,
∴,
∵,
∴,
∴.
一、单选题
1.已知的半径为,圆心到直线的距离为,则直线与的位置关系为 ( )
A.相交 B.相切 C.相离 D.无法确定
2.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm B.6cm C.7cm D.8cm
3.已知的半径为,点与圆心的距离为,则点与的位置关系是( )
A.点在内 B.点在上
C.点在外 D.点不在内
4.下列说法错误的是( )
A.圆上的点到圆心的距离相等 B.过圆心的线段是直径
C.直径是圆中最长的弦 D.半径相等的圆是等圆
5.点在半径为的外,则点到圆心的距离与的关系是( )
A. B. C. D.
6.已知在中,半径,弦,则的值不可以是( )
A.6 B.8
C.10 D.12
7.下列说法中,不正确的是( )
A.圆既是轴对称图形又是旋转对称图形
B.一个圆的直径的长是它半径的2倍
C.圆的每一条直径都是它的对称轴
D.直径是圆的弦,但半径不是弦
8.如图,在直角中,,则以为圆心,分别为半径的圆形成一个圆环,则该圆环的面积为( ).
A. B. C. D.
二、填空题
9.如图,AB是⊙O的一条弦,AB=6,圆心O到AB的距离为4,则⊙O的半径为_____.
10.如图,AD是⊙O的直径.
(1)如图1,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是_____,∠B2的度数是_____;
(2)如图2,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,则∠B3的度数是_____;
(3)如图3,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,则∠Bn的度数是_________(用含n的代数式表示∠Bn的度数).
11.一个半径为2cm的圆,其最长的弦的长度为_______.
12.已知两圆半径分别为4cm和1cm,若两圆相切,则两圆的圆心距为__cm
13.圆中最长的弦是_____.
14.半径为R的圆的周长是____________.
15.在Rt△ABC中,两直角边的长分别为6和8,则这个三角形的外接圆的直径长为__.16.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是点________________.
三、解答题
17.已知:如图,线段AB=8,以A为圆心,5为半径作圆A,点C在⊙A上,过点C作CD∥AB交⊙A于点D(点D在C右侧),联结BC、AD.
(1)若CD=6,求四边形ABCD的面积;
(2)设CD=x,BC=y,求y与x的关系式及x的取值范围;
(3)设BC的中点为M,AD的中点为N,MN∥CD,线段MN交⊙A于点E,联结CE,当CD取何值时,CE∥AD.
18.已知点P、Q,且PQ=4cm,
(1)画出下列图形:到点P的距离等于2cm的点的集合;到点Q的距离等于3cm的点的集合.
(2)在所画图中,到点P的距离等于2cm,且到点Q的距离等于3cm的点有几个?请在图中将它们表示出来.
19.已知:如图,在中,是直径,为不是直径的弦,求证:是中最长的弦.
20.如图,在△ABC中,∠ACB=90°,∠A=40°;以C为圆心、CB为半径的圆交AB于点D,求∠ACD的度数.
21.如图所示,在四边形ABCD ,∠B=∠D=90°,求证:A、B、C、D四点在同一个圆上.
22.如图,AB、AC是⊙O的两条弦,且AB=AC.求证:∠1=∠2.
23.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线相交于点E.已知AB=2DE,∠E=18°.试求∠AOC的度数.
24.以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,若BC=12,CD=5.求⊙A的半径r的取值范围.
25.已知两点A、B和直线l,求作一圆,使之经过A、B两点,且圆心在直线l上.
26.如图,CD是的直径,点A在DC的延长线上,AE交于点B,AB等于的半径,,求的度数.
答案
一、单选题
B.A.A.B.D.D.C.B.
二、填空题
9.5.
10.22.5° 67.5° 75°
11.4cm.
12.5或3.
13.直径.
14.2πR.
15.10.
16.Q.
三、解答题
17.(1)作AH⊥CD于H,如图,
则CH=DH=CD=×6=3,
在Rt△AHD中,∵AD=5,DH=3,
∴AH==4,
∴四边形ABCD的面积=(CD+AB) AH=×(6+8)×4=28;
(2)作CP⊥AB于P,如图1,
∵AH⊥CD,CD=x
∴CH=DH=x,
∴AP=CH=x,
∴BP=AB-AP=8-x,
在Rt△PAC中,∵AC2=AP2+CP2,
∴CP2=25-x2,
在Rt△BPC中,∵BC2=BP2+CP2,
∴y2=(8-x)2+25-x2=89-8x,
∴y=(0<x<10);
(3)设AH交MN于点F,连结AE,如图2,
∵CD∥AB,CD≠AB,
∴四边形ABCD为梯形,
∵BC的中点为M,AD的中点为N,
∴MN为梯形ABCD的中位线,
∴MN∥CD,
∵CE∥AD,
∴四边形CEND为平行四边形,
∴DC=NE=x,
∵FN∥CD,N点为AD的中点,
∴FN为△AHD的中位线,
∴FN=DH=x,
∴EF=x-x=x,
在Rt△AEF中,AF2=AE2-EF2,
在Rt△AFN中,AF2=AN2-NF2,
∴AE2-EF2=AN2-NF2,即52-(x)2=()2-(x)2,解得x=.
即当CD为时,CE∥AD.
18.
解:(1)到点P的距离等于2cm的点的集合图中⊙P;到点Q的距离等于3cm的点的集合图中⊙Q.
(2)到点P的距离等于2cm,且到点Q的距离等于3cm的点有2个,图中C、D.
19.
证明:如图,连接,,
、、、是圆的半径,
.
是圆的直径,
.
、、是三角形的三边,
.
即.
是中最长的弦.
20.
解:连接CD,∵∠ACB=90°,∠A=40°,
∴∠B=50°,
∵CD=CB,
∴∠BCD=180°-2×50°=80°,
∴∠ACD=90°-80°=10°.
故答案为10°.
21.
证明:连AC,取AC的中点O,连接OB、OD,
∵∠B=∠D=90°,
∴OB=AC,OD=AC.即OB=OA=OC=OD,
∴ A、B、C、D四点在同一圆上.
22.
连接OB、OC.
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS).
∴∠1=∠2.
23.
连接OD,
∵AB=2DE,AB=2OD,
∴OD=DE,∴∠DOE=∠E,
∴∠ODC=2∠E=36°,
∵OC=OD,∴∠C=∠ODC=36°,
∴∠AOC=∠C+∠E=54°
24.
解:根据题意画出图形如下所示:
∵AB=CD=5,AD=BC=12,
根据矩形的性质和勾股定理得到:AC==13.
∵AB=5,AD=12,AC=13,
而A,C,D中至少有一个点在⊙A内,且至少有一个点在⊙A外,
∴点B在⊙A内,点C在⊙A外.
∴5<r<13.
故答案为:5<r<13.
25.
解:连接AB,作线段AB的垂直平分线交直线于点O.以点O为圆心,AO为半径作圆,
则⊙O即为所求,
26.
解:∵AB等于的半径,
∴,
∴
∵
∴
∵,
∴,
∵,
∴,
∴.
同课章节目录
