九年级数学上册试题 3.1圆习题-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 3.1圆习题-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 470.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 22:52:46 | ||
图片预览




文档简介
3.1圆
一、单选题
1.已知在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,CM是它的中线,以C为圆心,5cm为半径作⊙C,则点M与⊙C的位置关系为( )
A.点M在⊙C上 B.点M在⊙C内 C.点M在⊙C外 D.点M不在⊙C内
2.平面上有四个点,过其中任意3个点一共能确定圆的个数为( )
A.0或3或4 B.0或1或3 C.0或1或3或4 D.0或1或4
3.下列命题:半圆是中心对称图形;相等的圆心角所对的弧相等;平分弦的直径垂直于弦;圆内两条非直径的相交弦不能互相平分,其中正确的有( )
A.个 B.个 C.个 D.个
4.在平面直角坐标系中,⊙O的圆心在点(1,0),半径为2,则下面各点在⊙O上的是( )
A.(2,0) B.(0,2) C.(0,) D.(,0)5.如图是由4个边长为a的正六边形组成的网格图,每个顶点均为格点,若该图中到点A的距离超过3的格点有且仅有6个,则a的取值范围为( )
A. B. C. D.
6.如图,、是上的两个点,是直径,若,则等于( )
A. B. C. D.
7.已知点O是△ABC的外心,作正方形OCDE,下列说法:①点O是△AEB的外心;②点O是△ADC的外心;③点O是△BCE的外心;④点O是△ADB的外心.其中一定不成立的说法是( )
A.②④ B.①③ C.②③④ D.①③④
8.下列图形中,面积最大的是( )
A.边长为6的正三角形; B.长分别为2.5、6、6.5的三角形;
C.半径为的圆; D.对角线长为6和8的菱形;
二、填空题
9.如图,在矩形纸片中,,,点是的中点,点是边上的一个动点,将△沿所在直线翻折,得到,则线段的最小值是___________.
10.如图,P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,若x、y都是整数,则这样的点共有_____个.
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为___.
12.如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为_______.
13.如图,矩形和正方形中,,,正方形绕点旋转过程中,线段的最小值为______.
14.点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,则动点M到达A101点处所需时间为____秒.
15.下列命题:①长度相等的弧是等弧;②半圆既包括圆弧又包括直径;③相等的圆心角所对的弦相等;④外心在三角形的一条边上的三角形是直角三角形,其中正确的命题有_________.
16.在一个圆中,有个圆心角为160°的扇形,则这个扇形的面积是整个圆面积的________.
三、解答题
17.已知:如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E两点.
(1)当△ABC为等边三角形时,则图1中△ODE的形状是 ;
(2)若A=60°,AB≠AC(如图2),则(1)的结论是否还成立?请说明理由.
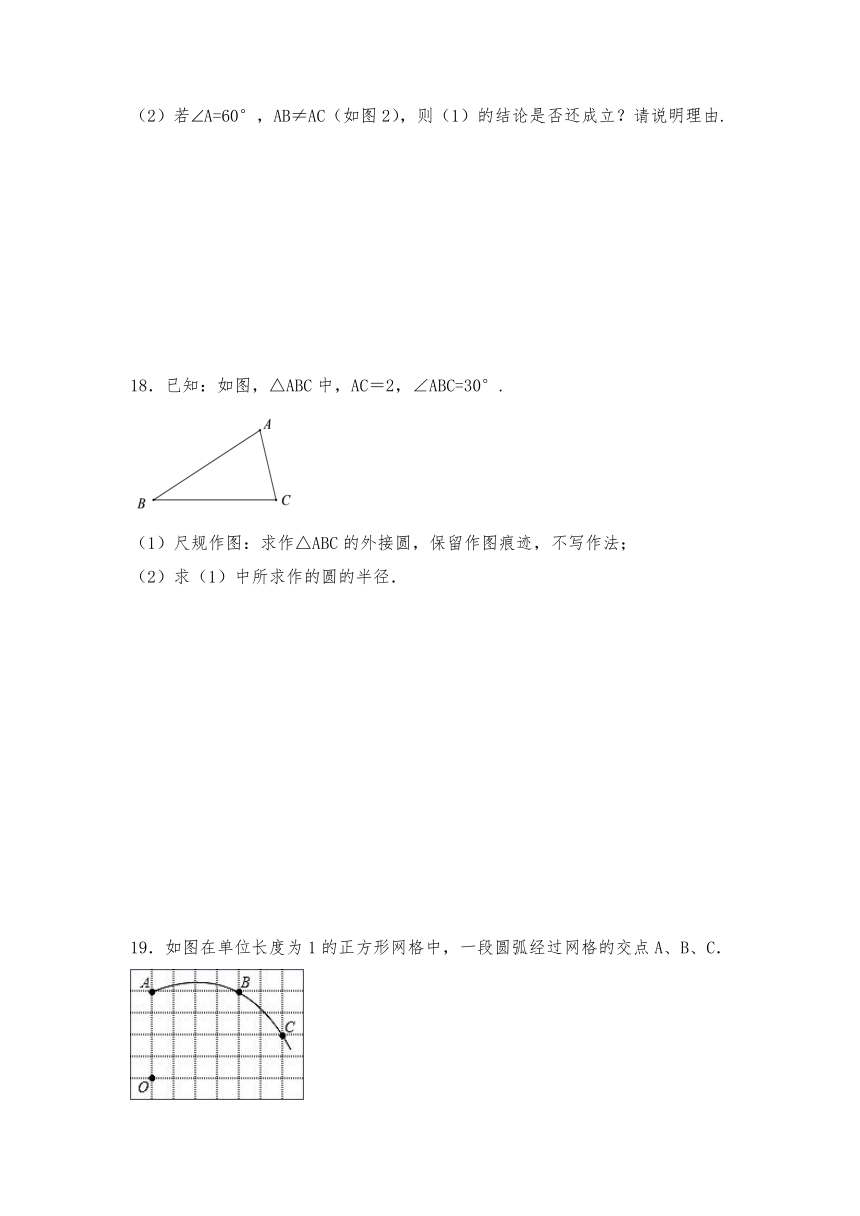
18.已知:如图,△ABC中,AC=2,∠ABC=30°.
(1)尺规作图:求作△ABC的外接圆,保留作图痕迹,不写作法;
(2)求(1)中所求作的圆的半径.
19.如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,只借助直尺确定该圆弧所在圆的圆心D,并连接AD、CD.(保留作图痕迹,不写作法)
(2)请在(1)的基础上,完成下列填空与计算:
①写出点的坐标:C 、D ;
②⊙D的半径= ;(结果保留根号)
③求扇形ADC的面积.(结果保留π)
20.如图,AB 是⊙O 的弦,AB=5cm,点 P 是弦 AB 上的一个定点,点 C 是弧 AB 上的一 个动点,连接 CP 并延长,交⊙O 于点 D.
小明根据学习函数的经验,分别对 AC,PC,PD 长度之间的关系进行了探究.
下面是小明的探究过程:
(1)对于点 C 在弧 AB 上的不同位置,画图、测量,得到了线段 AC,PC,PD 的长度的 几组值,如下表:
位置 1 位置 2 位置 3 位置 4 位置 5 位置 6 位置 7 位置 8 位置 9
AC/cm 0 0.37 1.00 1.82 2.10 3.00 3.50 3.91 5.00
PC/cm 1.00 0.81 0.69 0.75 1.26 2.11 2.50 3.00 4.00
PD/cm 4.00 5.00 5.80 6.00 3.00 1.90 1.50 1.32 1.00
在 AC,PC,PD 的长度这三个量中,确定___的长度是自变量,其他两条线段的长度都是这个自变量的函数;
(2)请你在同一平面直角坐标系 xOy 中, 画(1)中所确定的两个函数的图象;
(3)结合函数图象,解决问题:
①当 PC=PD 时,AC 的长度约为 cm;
②当△APC 为等腰三角形时,PC 的长度约为 cm.
21.如图, AB 是半圆O的直径, AD 和 BC 是它的两条切线,切点分别为 A 、B ,CO平分∠BCD.
(1)求证:CD是半圆O的切线;
(2)若AD=2 , CD=5 ,求 BC 的长.
22.如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合).试判断PA、PC、PB的大小关系,并说明理由.
23.如图,等腰中,,,平分交于,若点为外一点,且,判断和的位置关系.
24.已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°
(1)如图①,求∠DAC的大小;
(2)如图②,若⊙O的半径为4,求DE的长.
25.作图题:(保留作图痕迹,不写做法)
(1)已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心O。
(2)考古学家在考古过程中发现一个圆盘,但是因为历史悠久,已经有一部分缺失,如图所示.现希望复原圆盘,需要先找到圆盘的圆心,才能继续完成后续修复工作.请利用直尺(无刻度)和圆规,在图中找出圆心O.
答案
一、单选题
A.C.C.C.A.B.A.D.
二、填空题
9..
10.12个
11.4或2cm
12..
13.
14.(101+5050π)
15.②④.
16..
三、解答题
17.解:
△ODE为等边三角形
证明:∵△ABC为等边三角形,
∴B=C=60°.
∵OB=OC=OD=OE,
∴△OBD,△OEC均为等边三角形.
∴BOD=COE=60°.
∴DOE=60°.
∵OD=OE,
∴△ODE为等边三角形.
(2)答:成立.
证明:如图:连接CD
∵BC为⊙O直径,
∴BDC=90°,
∴ADC=90°.
∵A=60°,
∴ACD=30°.
∴DOE=60°.
∵OD=OE,
∴△DOE为等边三角形.
18.
(1)作法如下:
①作线段AB的垂直平分线;
②作线段BC的垂直平分线;
③以两条垂直平分线的交点O为圆心,OA长为半圆画圆,则圆O即为所求作的圆.
(2)连接OA,OB.
∵AC=2,∠ABC=30°,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴圆的半径是2,
19.
(1)根据题意画出相应的图形,如图所示:
(2)①根据图形得:C(6,2),D(2,0);
②在Rt△AOD中,OA=4,OD=2,
根据勾股定理得:AD=,
则⊙D的半径为;
③∵AD=CD,AO=DF=4,OD=CF=2,
∴△AOD≌△DFC,
∴∠ADO=∠DCF,
∴∠ADO+∠CDF=∠DCF +∠CDF=90°,
则∠ADC=90°,
∴S扇形ADC=
20.
解:(1)由于PC和PD随着AC的变化而变化,
∴确定AC的长度是自变量,其他两条线段的长度都是这个自变量的函数,
故答案为:AC;
(2)函数图象如图所示:
(3)①由函数图象得:当PC=PD时,AC的长度约为2.9cm;
②∵当AC=0时,点A和点C重合,此时PC=1cm,
∴AP=1cm,
当AP=AC=1cm时,由表格得,PC=0.69cm,
当AP=PC=1cm时,则PC=1cm,
当AC=PC时,如图,由函数图象得,PC≈0.8cm,
综上所述,PC的长度约为0.69cm或1cm或0.8cm.
21.(1)如图所示:过点O作OE⊥DC,垂足为E.
∵BC是圆0的切线,
∴OB⊥BC.
∴∠CEC=∠OBC=90°.
∵CO平分∠ECB,
∴∠ECO=∠BCO.
在△ECO和△BCO中,
,
∴ECO≌△BCO.
∴OE=OB.
∵OE⊥DC,OE=OB,
∴DC是圆O的切线.
(2)∵AD、DC、CB是圆的切线,
∴DE=DA,EC=CB.
∴BC=DC-AD=5-2=3.
22.当点P与点O重合时,PA=PB=PC,
当点P在OA上时,PA<PC<PB.
理由:连接OC,
在△POC中,OC-OP<PC<OP+OC,
∵OA=OB=OC,
∴OA-OP<PC<OP+OB,∴PA<PC<PB,
同理,当P点在OB上时,PB<PC<PA.
23..
理由如下:
过、、三点作圆,与射线相交于点,连接、,如图所示,
则、、、四点共圆,
所以根据圆内接四边形的性质可得.
∵,,
∴,
∴.
∵,
∴,
∴点与点重合,
∴、、、四点共圆,
∴根据圆周角定理可得,即.
24.(1)连接OC,如图①,
∵DC切⊙O于点C,∴OC⊥DC,又∵AD⊥DC,∴AD∥OC,∴∠DAC=∠ACO,∵OA=OC,∴∠OCA=∠CAB=30°,∴∠DAC=30°;
(2)连OE,OC,如图②,
∵∠EOC=2∠DAC=60°,∴△OEC为等边三角形,∴EC=OE=4,∠OCE=60°,∴∠DCE=30°,
∴DE=CE=2.
25.(1)如图所示,点O即为对称中心.理由如下:
∵四边形ABCD与四边形EFGH成中心对称,∴BF过对称中心,CG过对称中心,∴BF、CG的交点即为对称中心.
(2)如图所示,点O即为所求作的圆心;
一、单选题
1.已知在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,CM是它的中线,以C为圆心,5cm为半径作⊙C,则点M与⊙C的位置关系为( )
A.点M在⊙C上 B.点M在⊙C内 C.点M在⊙C外 D.点M不在⊙C内
2.平面上有四个点,过其中任意3个点一共能确定圆的个数为( )
A.0或3或4 B.0或1或3 C.0或1或3或4 D.0或1或4
3.下列命题:半圆是中心对称图形;相等的圆心角所对的弧相等;平分弦的直径垂直于弦;圆内两条非直径的相交弦不能互相平分,其中正确的有( )
A.个 B.个 C.个 D.个
4.在平面直角坐标系中,⊙O的圆心在点(1,0),半径为2,则下面各点在⊙O上的是( )
A.(2,0) B.(0,2) C.(0,) D.(,0)5.如图是由4个边长为a的正六边形组成的网格图,每个顶点均为格点,若该图中到点A的距离超过3的格点有且仅有6个,则a的取值范围为( )
A. B. C. D.
6.如图,、是上的两个点,是直径,若,则等于( )
A. B. C. D.
7.已知点O是△ABC的外心,作正方形OCDE,下列说法:①点O是△AEB的外心;②点O是△ADC的外心;③点O是△BCE的外心;④点O是△ADB的外心.其中一定不成立的说法是( )
A.②④ B.①③ C.②③④ D.①③④
8.下列图形中,面积最大的是( )
A.边长为6的正三角形; B.长分别为2.5、6、6.5的三角形;
C.半径为的圆; D.对角线长为6和8的菱形;
二、填空题
9.如图,在矩形纸片中,,,点是的中点,点是边上的一个动点,将△沿所在直线翻折,得到,则线段的最小值是___________.
10.如图,P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,若x、y都是整数,则这样的点共有_____个.
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为___.
12.如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为_______.
13.如图,矩形和正方形中,,,正方形绕点旋转过程中,线段的最小值为______.
14.点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,则动点M到达A101点处所需时间为____秒.
15.下列命题:①长度相等的弧是等弧;②半圆既包括圆弧又包括直径;③相等的圆心角所对的弦相等;④外心在三角形的一条边上的三角形是直角三角形,其中正确的命题有_________.
16.在一个圆中,有个圆心角为160°的扇形,则这个扇形的面积是整个圆面积的________.
三、解答题
17.已知:如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E两点.
(1)当△ABC为等边三角形时,则图1中△ODE的形状是 ;
(2)若A=60°,AB≠AC(如图2),则(1)的结论是否还成立?请说明理由.
18.已知:如图,△ABC中,AC=2,∠ABC=30°.
(1)尺规作图:求作△ABC的外接圆,保留作图痕迹,不写作法;
(2)求(1)中所求作的圆的半径.
19.如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,只借助直尺确定该圆弧所在圆的圆心D,并连接AD、CD.(保留作图痕迹,不写作法)
(2)请在(1)的基础上,完成下列填空与计算:
①写出点的坐标:C 、D ;
②⊙D的半径= ;(结果保留根号)
③求扇形ADC的面积.(结果保留π)
20.如图,AB 是⊙O 的弦,AB=5cm,点 P 是弦 AB 上的一个定点,点 C 是弧 AB 上的一 个动点,连接 CP 并延长,交⊙O 于点 D.
小明根据学习函数的经验,分别对 AC,PC,PD 长度之间的关系进行了探究.
下面是小明的探究过程:
(1)对于点 C 在弧 AB 上的不同位置,画图、测量,得到了线段 AC,PC,PD 的长度的 几组值,如下表:
位置 1 位置 2 位置 3 位置 4 位置 5 位置 6 位置 7 位置 8 位置 9
AC/cm 0 0.37 1.00 1.82 2.10 3.00 3.50 3.91 5.00
PC/cm 1.00 0.81 0.69 0.75 1.26 2.11 2.50 3.00 4.00
PD/cm 4.00 5.00 5.80 6.00 3.00 1.90 1.50 1.32 1.00
在 AC,PC,PD 的长度这三个量中,确定___的长度是自变量,其他两条线段的长度都是这个自变量的函数;
(2)请你在同一平面直角坐标系 xOy 中, 画(1)中所确定的两个函数的图象;
(3)结合函数图象,解决问题:
①当 PC=PD 时,AC 的长度约为 cm;
②当△APC 为等腰三角形时,PC 的长度约为 cm.
21.如图, AB 是半圆O的直径, AD 和 BC 是它的两条切线,切点分别为 A 、B ,CO平分∠BCD.
(1)求证:CD是半圆O的切线;
(2)若AD=2 , CD=5 ,求 BC 的长.
22.如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合).试判断PA、PC、PB的大小关系,并说明理由.
23.如图,等腰中,,,平分交于,若点为外一点,且,判断和的位置关系.
24.已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°
(1)如图①,求∠DAC的大小;
(2)如图②,若⊙O的半径为4,求DE的长.
25.作图题:(保留作图痕迹,不写做法)
(1)已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心O。
(2)考古学家在考古过程中发现一个圆盘,但是因为历史悠久,已经有一部分缺失,如图所示.现希望复原圆盘,需要先找到圆盘的圆心,才能继续完成后续修复工作.请利用直尺(无刻度)和圆规,在图中找出圆心O.
答案
一、单选题
A.C.C.C.A.B.A.D.
二、填空题
9..
10.12个
11.4或2cm
12..
13.
14.(101+5050π)
15.②④.
16..
三、解答题
17.解:
△ODE为等边三角形
证明:∵△ABC为等边三角形,
∴B=C=60°.
∵OB=OC=OD=OE,
∴△OBD,△OEC均为等边三角形.
∴BOD=COE=60°.
∴DOE=60°.
∵OD=OE,
∴△ODE为等边三角形.
(2)答:成立.
证明:如图:连接CD
∵BC为⊙O直径,
∴BDC=90°,
∴ADC=90°.
∵A=60°,
∴ACD=30°.
∴DOE=60°.
∵OD=OE,
∴△DOE为等边三角形.
18.
(1)作法如下:
①作线段AB的垂直平分线;
②作线段BC的垂直平分线;
③以两条垂直平分线的交点O为圆心,OA长为半圆画圆,则圆O即为所求作的圆.
(2)连接OA,OB.
∵AC=2,∠ABC=30°,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴圆的半径是2,
19.
(1)根据题意画出相应的图形,如图所示:
(2)①根据图形得:C(6,2),D(2,0);
②在Rt△AOD中,OA=4,OD=2,
根据勾股定理得:AD=,
则⊙D的半径为;
③∵AD=CD,AO=DF=4,OD=CF=2,
∴△AOD≌△DFC,
∴∠ADO=∠DCF,
∴∠ADO+∠CDF=∠DCF +∠CDF=90°,
则∠ADC=90°,
∴S扇形ADC=
20.
解:(1)由于PC和PD随着AC的变化而变化,
∴确定AC的长度是自变量,其他两条线段的长度都是这个自变量的函数,
故答案为:AC;
(2)函数图象如图所示:
(3)①由函数图象得:当PC=PD时,AC的长度约为2.9cm;
②∵当AC=0时,点A和点C重合,此时PC=1cm,
∴AP=1cm,
当AP=AC=1cm时,由表格得,PC=0.69cm,
当AP=PC=1cm时,则PC=1cm,
当AC=PC时,如图,由函数图象得,PC≈0.8cm,
综上所述,PC的长度约为0.69cm或1cm或0.8cm.
21.(1)如图所示:过点O作OE⊥DC,垂足为E.
∵BC是圆0的切线,
∴OB⊥BC.
∴∠CEC=∠OBC=90°.
∵CO平分∠ECB,
∴∠ECO=∠BCO.
在△ECO和△BCO中,
,
∴ECO≌△BCO.
∴OE=OB.
∵OE⊥DC,OE=OB,
∴DC是圆O的切线.
(2)∵AD、DC、CB是圆的切线,
∴DE=DA,EC=CB.
∴BC=DC-AD=5-2=3.
22.当点P与点O重合时,PA=PB=PC,
当点P在OA上时,PA<PC<PB.
理由:连接OC,
在△POC中,OC-OP<PC<OP+OC,
∵OA=OB=OC,
∴OA-OP<PC<OP+OB,∴PA<PC<PB,
同理,当P点在OB上时,PB<PC<PA.
23..
理由如下:
过、、三点作圆,与射线相交于点,连接、,如图所示,
则、、、四点共圆,
所以根据圆内接四边形的性质可得.
∵,,
∴,
∴.
∵,
∴,
∴点与点重合,
∴、、、四点共圆,
∴根据圆周角定理可得,即.
24.(1)连接OC,如图①,
∵DC切⊙O于点C,∴OC⊥DC,又∵AD⊥DC,∴AD∥OC,∴∠DAC=∠ACO,∵OA=OC,∴∠OCA=∠CAB=30°,∴∠DAC=30°;
(2)连OE,OC,如图②,
∵∠EOC=2∠DAC=60°,∴△OEC为等边三角形,∴EC=OE=4,∠OCE=60°,∴∠DCE=30°,
∴DE=CE=2.
25.(1)如图所示,点O即为对称中心.理由如下:
∵四边形ABCD与四边形EFGH成中心对称,∴BF过对称中心,CG过对称中心,∴BF、CG的交点即为对称中心.
(2)如图所示,点O即为所求作的圆心;
同课章节目录
