九年级数学上册试题 3.2图形的旋转 习题-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 3.2图形的旋转 习题-浙教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 929.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 22:53:31 | ||
图片预览





文档简介
3.2图形的旋转
一、单选题
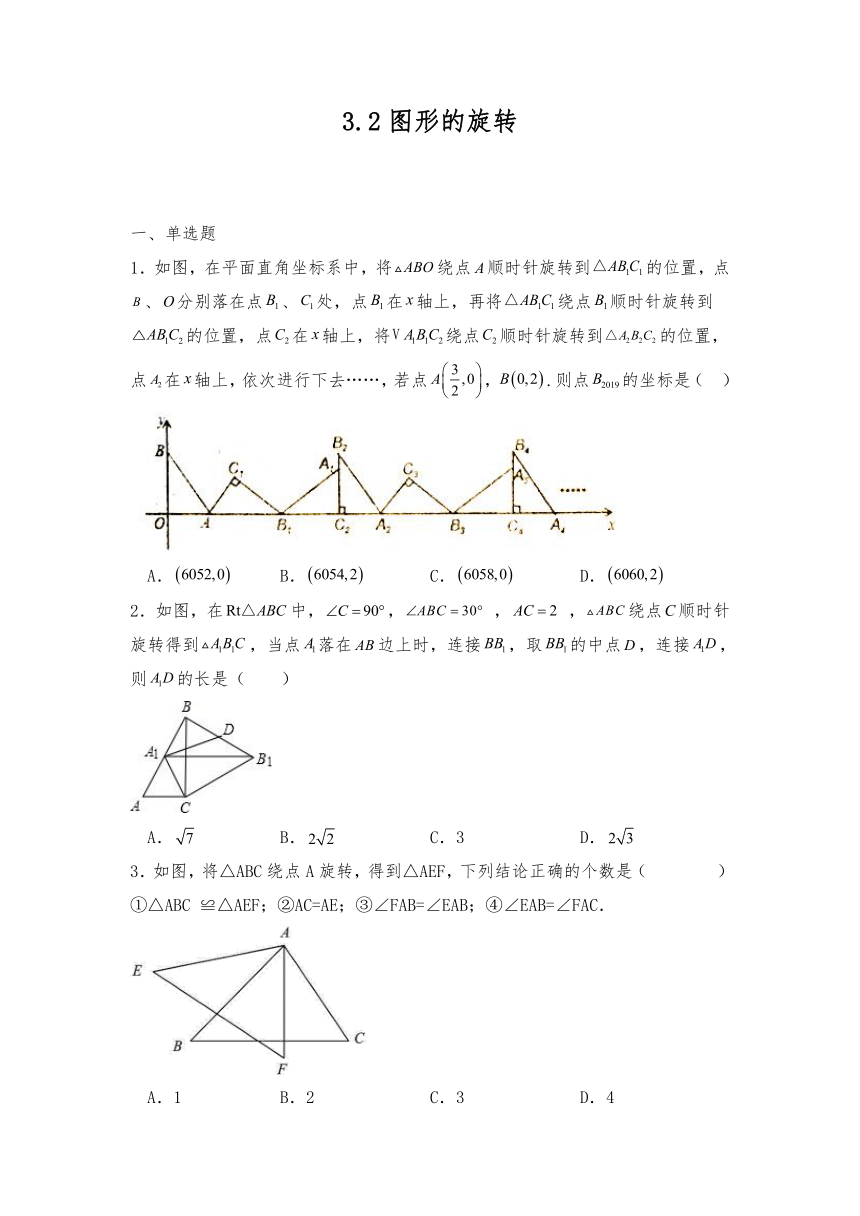
1.如图,在平面直角坐标系中,将绕点顺时针旋转到的位置,点、分别落在点、处,点在轴上,再将绕点顺时针旋转到的位置,点在轴上,将绕点顺时针旋转到的位置,点在轴上,依次进行下去……,若点,.则点的坐标是( )
A. B. C. D.
2.如图,在中,, , ,绕点顺时针旋转得到,当点落在边上时,连接,取的中点,连接,则的长是( )
A. B. C.3 D.
3.如图,将△ABC绕点A旋转,得到△AEF,下列结论正确的个数是( )
①△ABC ≌△AEF;②AC=AE;③∠FAB=∠EAB;④∠EAB=∠FAC.
A.1 B.2 C.3 D.4
4.如图,直线与x轴、y轴分别相交于点A、B,过点B作,使,将绕点O顺时针旋转,每次旋转,则第2021次旋转结束时,点C的对应点落在反比例函数的图象上,则k的值为( )
A. B.4 C. D.6
5.如图,将绕着点顺时针旋转后得到,若,则的度数是( )
A. B. C. D.
6.将正方体骰子(相对面上的点数1和6、2和5、3和4)放置于水平桌面上,如图1.在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换,若骰子的初始位置为图1所示的状态,那么按上述规则连续完成4次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.1
7.如图,∠ABC=20°,将△ABC绕点B顺时针旋转130°得到△EBF.若点A,F,E在同一条直线上,则∠AFB的度数是( )
A.35° B.40° C.45° D.50°
8.如图,点的坐标是,点的坐标是,为的中点,将绕点逆时针旋转后得到,若反比例函数的图象恰好经过的中点,则的值是( )
A.24 B.25 C.26 D.30
二、填空题
9.如图,菱形的对角线交于点,将绕着点旋转得到,若,则菱形的边长是_______.
10.如图,在△ABC 中,∠ACB 为钝角,边 AC 绕点 A 沿逆时针方向旋转 90°得到AD,边 BC 绕点 B 沿顺时针方向旋转 90°得到 BE,作 DM⊥AB 于点 M,EN⊥AB于 点 N, 若 AB=10,EN=4, 则 DM=__________.
11.如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360°),得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值和最大值的和为_____.
12.如图,一副含30°和45°角的三角板和拼合在个平面上,边与重合,.当点从点出发沿方向滑动时,点同时从点出发沿射线方向滑动.当点从点滑动到点时停止运动,连接,则的面积最大值为__________.
13.在中,,,将绕点旋转,使点落在原的点处,此时点落在点处,延长线段,交原的边的延长线于点,则的度数为____度.
14.如图平面直角坐标系中,的顶点坐标分别为,,,点绕点旋转得到点,点绕点旋转得到点,点绕点旋转得到点,点绕点旋转得到点,…,按此作法进行下去,则点的坐标为_____________.
15.如图,将绕直角顶点逆时针旋转,使顶点的对应点落在边上,点的对应点与点的连线交于点,则的度数为_______.
16.如图,在△ABC中,∠BAC=35°,将△ABC绕点A顺时针方向旋转50°,得到△AB′C′,则∠B′AC的度数是 .
三、解答题
17.如图,在四边形ABCD中,AB=AD,∠B+∠D=180 ,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.
18.如图,方格纸中的每格都是边长为1的正方形,将(顶点都是正方形的顶点)绕点按逆时针方向旋转得到.
(1)在所给的图形中画出;
(2)线段AA1的长为 ;
(3)以O、B、A、A1为顶点的四边形的面积为
19.如图,是绕点顺时针旋转后得到的图形,若点恰好落在上,且,求的度数.
20.某数学活动小组在一次活动中,对一个数学问题作如下研究:
(问题呈现)
(1)如图1,中分别以为边向外作等腰和等腰,使,,,连结,试猜想与的大小关系,并说明理由.
(问题再探)
(2)如图2,中分别以为边向外作等腰和等腰,,连结,若,求的长.
(问题拓展)
(3)如图3,四边形中,连结,,,,,,请直接写出的长.
21.在中,,.
(1)直接写出的大小为______.(用含的式子表示)
(2)当时,将线段绕点逆时针旋转得到线段,连接、.
①求证:;
②当,求的度数.
22.综合与实践
问题情境
从“特殊到一般”是数学探究的常用方法之,类比特殊图形中的数量关系和探究方法可以发现一般图形具有的普遍规律.
如图1,在中,,,为边上的中线,为上一点,将以点为旋转中心,逆时针旋转90°得到,的延长线交线段于点.探究线段,,之间的数量关系.
数学思考
(1)请你在图1中证明;
特例探究
(2)如图2,当垂直于时,求证:;
类比再探
(3)请判断(2)的结论在图1中是否仍然成立?若成立,请证明;若不成立,请说明理由.
23.如图1,四根长度一定的木条,其中AB=6cm,CD=15cm,将这四根木条用小钉绞合在一起,构成一个四边形ABCD(在A、B、C、D四点处是可以活动的).现固定AB边不动,转动这个四边形,使它的形状改变,在转动的过程中有以下两个特殊位置.
位置一:当点D在BA的延长线上时,点C在线段AD上(如图2);
位置二:当点C在AB的延长线上时,∠C=90°.
(1)在图2中,若设BC的长为,请用的代数式表示AD的长;
(2)在图3中画出位置二的准确图形;(各木条长度需符合题目要求)
(3)利用图2、图3求图1的四边形ABCD中,BC、AD边的长.
24.甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
任务要求:
(1)请你在图1中画出旋转后的图形
甲、乙、丙三名同学又继续探索:
在正方形ABCD中,∠EAF=45°,点F为BC上一点,点E为DC上一点,∠EAF的两边AE、AF分别与直线BD交于点M、N.连接EF
甲发现:线段BF,EF,DE之间存在着关系式EF=BF+DE;
乙发现:△CEF的周长是一个恒定不变的值;
丙发现:线段BN,MN,DM之间存在着关系式BN2+DM2=MN2
(2)现请你参与三位同学的研究工作中来,你认为三名同学中哪个的发现是正确的,并说明你的理由.
25.通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的,下面是一个案例,请补充完整.
原题;如图①,点分别在正方形的边上,,连接,则,试说明理由,
(1)(思路梳理)
∵,∴把绕点A逆时针旋转至,可使与重合,∵,∴,即:点共线,根据“”,易证_______,得;
(2)(类比引申)
如图②,四边形中,,点分别在上,,若都不是直角,则当与满足等量关系__________时,仍有;
(3)(联想拓展)
如图③,在中,,点均在边上,且,猜想应满足的等量关系,并写出推理过程.
26.如图,点O是等边ABC内一点,将CO绕点C顺时针旋转60°得到CD,连接OD,AO,BO,AD.
(1)求证:BCO≌ACD.
(2)若OA=10,OB=8,OC=6,求∠BOC的度数.
答案
一、单选题
C.A.B.D.B.B.C.C.
二、填空题
9.
10.6
11.﹣1
12..
13.30°.
14..
15.105.
16.15°.
三、解答题
17.
证明:如图将△ADF顺时针旋转得到△ABG,使得AD与AB重合,
则△ADF≌△ABG,
∴∠FAG=∠BAD,AF=AG,DF=GB,
∵,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=EF,
∵GE=GB+BE=DF+BE,
∴EF=BE+FD.
18.
解:(1)先分别画出点,再顺次连接点即可得到,如图所示:
(2)由题意得:在中,,
,
由旋转的性质得:,
则在中,,
故答案为:;
(3)以、、、为顶点的四边形的面积为,
,
,
,
故答案为:.
19.
解:是绕点顺时针旋转后得到的图形,
,,
,
,
,
,
,
.
20.
解:(1),理由如下:
∵,
∴,
又∵,
,
∴,
∴;
(2)∵等腰和等腰,
∴,,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
在中,
,
∴;
(3)∵,,
∴△BCD是等边三角形,
连接BD,把△ABD绕点D逆时针旋转60°得到△ECD,连接AE,
则EC=AB=15,△ADE是等边三角形,
∴,,
∵,
∴,
在Rt△AEC中,
,
∴.
21.
解:(1)90°-α
∵ AB=AC,
∴∠ABC=(180°-∠BAC)
=(180°-α)
=90°-α
(2)①线段BC绕点B逆时针旋转60°得到线段BD则BC=BD, ∠DBC =60°
∴△BCD为等边三角形
∴ BD=CD
在△ABD和△ACD中,
∵AB =AC
BD= CD,
AD=AD
∴△ABD≌△ ACD(SSS)
②当α=40°时,
∵ AB=AC,∠ACB =∠ABC =90°-α=70°
∵△BCD为等边三角形
∴∠BCD =60°
∴∠ACD = ∠ACB-∠BCD = 10°
22.
(1)证明:根据旋转图形的性质,可得△AEC≌△BFC,
∴∠FBC=∠EAC.
又∵∠ADC=∠BDP,∠EAC+∠ADC=180°-∠ACD=90°,
∴∠BDP+∠FBC=90°,
∴∠BPD=180°-(∠BDP+∠FBC)=90°,
∴AP⊥BE.
(2)证明:∵∠CEP=∠EPF=∠ECF=90°,
∴四边形CEPF是矩形.
∵CE=CF
∴四边形CEPF是正方形.
∴CE=EP=FP.
又∵∠CDE=∠BDP,CD=BD,∠CED=∠BPD=90°
∴△CED≌△BPD,
∴CE=BP.
∴EP+FP=2CE=2BP.
(3)成立.
理由如下:过点C作CG⊥AD,垂足为G,CH⊥BP,垂足为H.
∵△BFC由△AEC逆时针90°旋转得到,
∴∠AEC=∠BFC,CE=CF,∠ECF=90°.
∵∠CEG+∠AEC=180°,∠CFH+∠BFC=180°,
∴∠CEG=∠CFH.
∵∠CGE=∠CHF=90°,
∴△CEG≌△CFH,
∴CH=CG,EG=FH.
∴EP+FP=GP+HP
∵∠CGP=∠GPH=∠H=90°,
∴四边形CGPH是正方形.
又(2)可知,GP+PH=2BP,
∴EP+PF=2BP.
23.
解:(1)∵在四边形ABCD的转动过程中,BC、AD边的长度始终保持不变,BC=x,
∴在图2中,AC=BC AB=x 6,AD=AC+CD=x+9.
(2)∴位置二的图见图3.
(3)∵在四边形ABCD转动的过程中,BC、AD边的长度始终保持不变,
∴在图3中,BC=x,AC=AB+BC=6+x,AD=x+9,
∵图3中,△ACD为直角三角形,∠C=90°,
由勾股定理得:AC2+CD2=AD2,
∴(6+x)2+152=(x+9)2,
整理,得6x=180,
解得x=30,
即BC=30,
∴AD=39.
24. 解:(1)画图如图1所示;
(2)甲、乙、丙三名同学的发现都是正确的;
①甲发现正确;理由如下:
如图2所示,
延长CB到K,使BK=DE,连AK,
∵四边形ABCD是正方形,
∴AB=AD,∠ABF=∠ABK=∠ADE=90°,
在△AKB和△AED中,,
∴△AKB≌△AED(SAS),
∴∠BAK=∠DAE,
∵∠BAF+∠DAE=45°,
∴∠BAF+∠BAK=45°,
即∠KAF=45°,
∴∠KAF=∠FAE,
在△AKF和△AEF中,,
∴△AKF≌△AEF(SAS),
∴KF=EF,
又∵BK=DE,
∴EF=BF+DE;
②乙发现正确;理由如下:
延长CB到K,使BK=DE,连接AK,如图2所示:
同①得:△AKB≌△AED,
∴∠BAK=∠DAE,
∵∠BAF+∠DAE=45°,
∴∠BAF+∠BAK=45°,
即∠KAF=45°,
∴∠KAF=∠FAE,
在△AKF和△AEF中,,
∴△AKF≌△AEF(SAS),
∴KF=EF,
又∵BK=DE,
∴EF=BF+DE;
△CEF周长=CF+CE+EF
=CF+CE+(BF+DE)
=(CF+BF)+(CE+DE)
=BC+DC=2a(定值);
③丙发现正确;理由如下:
如图3,在AK上截取AG=AM,连接BG,GN,
在△ABG和△ADM中,,
∴△ABG≌△ADM(SAS),
∴BG=DM,∠ABG=∠ADB=45°,
又∵∠ABD=45°,
∴∠GBD=90°,
∵∠BAF+∠DAE=45°,
∴∠KAF=45°,
∴∠KAF=∠FAE,
在△GAN和△NAM中,,
∴△GAN≌△NAM(SAS),
∴NG=MN,
∵∠GBD=90°,
∴BG2+BN2=NG2,
∴BN2+DM2=MN2;
综上所述:甲、乙、丙三名同学的发现都是正确的.
25.
解:(1) ∵,
把绕点逆时针旋转至,
可使与重合,
三点共线,
则
即
在与中
故答案为:;
(2)当时,仍有,理由如下:
∵,
把绕点逆时针旋转至,可使与重合,如图,
三点共线,
在与中
即
故答案为:;
(3)猜想:,理由如下,
证明:将绕点顺时针旋转,得到,如图,连接,则
,
在中
在与中
.
26.
(1)证明:∵CO绕点C顺时针旋转60°得到CD,
∴CO=CD,∠OCD=60°,
∵△ABC是等边三角形,
∴CA=CB,∠BCA=60°,
∴∠BCA=∠OCD,
∴∠BCO=∠ACD,
在△BCO和△ACD中,
,
∴△BCO≌△ACD(SAS).
(2)解:∵CO=CD,∠OCD=60°,
∴△OCD是等边三角形,
∴OD=OC=6.∠ODC=60°,
∵△BCO≌△ACD,
∴AD=OB=8,∠BOC=∠ADC,
∵OA=10,
∴OA2=AD2+OD2,
∴∠ADO=90°,
∴∠ADC=∠ADO+∠CDO=150°,
∴∠BOC=∠ADC=150°.
,
一、单选题
1.如图,在平面直角坐标系中,将绕点顺时针旋转到的位置,点、分别落在点、处,点在轴上,再将绕点顺时针旋转到的位置,点在轴上,将绕点顺时针旋转到的位置,点在轴上,依次进行下去……,若点,.则点的坐标是( )
A. B. C. D.
2.如图,在中,, , ,绕点顺时针旋转得到,当点落在边上时,连接,取的中点,连接,则的长是( )
A. B. C.3 D.
3.如图,将△ABC绕点A旋转,得到△AEF,下列结论正确的个数是( )
①△ABC ≌△AEF;②AC=AE;③∠FAB=∠EAB;④∠EAB=∠FAC.
A.1 B.2 C.3 D.4
4.如图,直线与x轴、y轴分别相交于点A、B,过点B作,使,将绕点O顺时针旋转,每次旋转,则第2021次旋转结束时,点C的对应点落在反比例函数的图象上,则k的值为( )
A. B.4 C. D.6
5.如图,将绕着点顺时针旋转后得到,若,则的度数是( )
A. B. C. D.
6.将正方体骰子(相对面上的点数1和6、2和5、3和4)放置于水平桌面上,如图1.在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换,若骰子的初始位置为图1所示的状态,那么按上述规则连续完成4次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.1
7.如图,∠ABC=20°,将△ABC绕点B顺时针旋转130°得到△EBF.若点A,F,E在同一条直线上,则∠AFB的度数是( )
A.35° B.40° C.45° D.50°
8.如图,点的坐标是,点的坐标是,为的中点,将绕点逆时针旋转后得到,若反比例函数的图象恰好经过的中点,则的值是( )
A.24 B.25 C.26 D.30
二、填空题
9.如图,菱形的对角线交于点,将绕着点旋转得到,若,则菱形的边长是_______.
10.如图,在△ABC 中,∠ACB 为钝角,边 AC 绕点 A 沿逆时针方向旋转 90°得到AD,边 BC 绕点 B 沿顺时针方向旋转 90°得到 BE,作 DM⊥AB 于点 M,EN⊥AB于 点 N, 若 AB=10,EN=4, 则 DM=__________.
11.如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360°),得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值和最大值的和为_____.
12.如图,一副含30°和45°角的三角板和拼合在个平面上,边与重合,.当点从点出发沿方向滑动时,点同时从点出发沿射线方向滑动.当点从点滑动到点时停止运动,连接,则的面积最大值为__________.
13.在中,,,将绕点旋转,使点落在原的点处,此时点落在点处,延长线段,交原的边的延长线于点,则的度数为____度.
14.如图平面直角坐标系中,的顶点坐标分别为,,,点绕点旋转得到点,点绕点旋转得到点,点绕点旋转得到点,点绕点旋转得到点,…,按此作法进行下去,则点的坐标为_____________.
15.如图,将绕直角顶点逆时针旋转,使顶点的对应点落在边上,点的对应点与点的连线交于点,则的度数为_______.
16.如图,在△ABC中,∠BAC=35°,将△ABC绕点A顺时针方向旋转50°,得到△AB′C′,则∠B′AC的度数是 .
三、解答题
17.如图,在四边形ABCD中,AB=AD,∠B+∠D=180 ,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.
18.如图,方格纸中的每格都是边长为1的正方形,将(顶点都是正方形的顶点)绕点按逆时针方向旋转得到.
(1)在所给的图形中画出;
(2)线段AA1的长为 ;
(3)以O、B、A、A1为顶点的四边形的面积为
19.如图,是绕点顺时针旋转后得到的图形,若点恰好落在上,且,求的度数.
20.某数学活动小组在一次活动中,对一个数学问题作如下研究:
(问题呈现)
(1)如图1,中分别以为边向外作等腰和等腰,使,,,连结,试猜想与的大小关系,并说明理由.
(问题再探)
(2)如图2,中分别以为边向外作等腰和等腰,,连结,若,求的长.
(问题拓展)
(3)如图3,四边形中,连结,,,,,,请直接写出的长.
21.在中,,.
(1)直接写出的大小为______.(用含的式子表示)
(2)当时,将线段绕点逆时针旋转得到线段,连接、.
①求证:;
②当,求的度数.
22.综合与实践
问题情境
从“特殊到一般”是数学探究的常用方法之,类比特殊图形中的数量关系和探究方法可以发现一般图形具有的普遍规律.
如图1,在中,,,为边上的中线,为上一点,将以点为旋转中心,逆时针旋转90°得到,的延长线交线段于点.探究线段,,之间的数量关系.
数学思考
(1)请你在图1中证明;
特例探究
(2)如图2,当垂直于时,求证:;
类比再探
(3)请判断(2)的结论在图1中是否仍然成立?若成立,请证明;若不成立,请说明理由.
23.如图1,四根长度一定的木条,其中AB=6cm,CD=15cm,将这四根木条用小钉绞合在一起,构成一个四边形ABCD(在A、B、C、D四点处是可以活动的).现固定AB边不动,转动这个四边形,使它的形状改变,在转动的过程中有以下两个特殊位置.
位置一:当点D在BA的延长线上时,点C在线段AD上(如图2);
位置二:当点C在AB的延长线上时,∠C=90°.
(1)在图2中,若设BC的长为,请用的代数式表示AD的长;
(2)在图3中画出位置二的准确图形;(各木条长度需符合题目要求)
(3)利用图2、图3求图1的四边形ABCD中,BC、AD边的长.
24.甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
任务要求:
(1)请你在图1中画出旋转后的图形
甲、乙、丙三名同学又继续探索:
在正方形ABCD中,∠EAF=45°,点F为BC上一点,点E为DC上一点,∠EAF的两边AE、AF分别与直线BD交于点M、N.连接EF
甲发现:线段BF,EF,DE之间存在着关系式EF=BF+DE;
乙发现:△CEF的周长是一个恒定不变的值;
丙发现:线段BN,MN,DM之间存在着关系式BN2+DM2=MN2
(2)现请你参与三位同学的研究工作中来,你认为三名同学中哪个的发现是正确的,并说明你的理由.
25.通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的,下面是一个案例,请补充完整.
原题;如图①,点分别在正方形的边上,,连接,则,试说明理由,
(1)(思路梳理)
∵,∴把绕点A逆时针旋转至,可使与重合,∵,∴,即:点共线,根据“”,易证_______,得;
(2)(类比引申)
如图②,四边形中,,点分别在上,,若都不是直角,则当与满足等量关系__________时,仍有;
(3)(联想拓展)
如图③,在中,,点均在边上,且,猜想应满足的等量关系,并写出推理过程.
26.如图,点O是等边ABC内一点,将CO绕点C顺时针旋转60°得到CD,连接OD,AO,BO,AD.
(1)求证:BCO≌ACD.
(2)若OA=10,OB=8,OC=6,求∠BOC的度数.
答案
一、单选题
C.A.B.D.B.B.C.C.
二、填空题
9.
10.6
11.﹣1
12..
13.30°.
14..
15.105.
16.15°.
三、解答题
17.
证明:如图将△ADF顺时针旋转得到△ABG,使得AD与AB重合,
则△ADF≌△ABG,
∴∠FAG=∠BAD,AF=AG,DF=GB,
∵,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=EF,
∵GE=GB+BE=DF+BE,
∴EF=BE+FD.
18.
解:(1)先分别画出点,再顺次连接点即可得到,如图所示:
(2)由题意得:在中,,
,
由旋转的性质得:,
则在中,,
故答案为:;
(3)以、、、为顶点的四边形的面积为,
,
,
,
故答案为:.
19.
解:是绕点顺时针旋转后得到的图形,
,,
,
,
,
,
,
.
20.
解:(1),理由如下:
∵,
∴,
又∵,
,
∴,
∴;
(2)∵等腰和等腰,
∴,,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
在中,
,
∴;
(3)∵,,
∴△BCD是等边三角形,
连接BD,把△ABD绕点D逆时针旋转60°得到△ECD,连接AE,
则EC=AB=15,△ADE是等边三角形,
∴,,
∵,
∴,
在Rt△AEC中,
,
∴.
21.
解:(1)90°-α
∵ AB=AC,
∴∠ABC=(180°-∠BAC)
=(180°-α)
=90°-α
(2)①线段BC绕点B逆时针旋转60°得到线段BD则BC=BD, ∠DBC =60°
∴△BCD为等边三角形
∴ BD=CD
在△ABD和△ACD中,
∵AB =AC
BD= CD,
AD=AD
∴△ABD≌△ ACD(SSS)
②当α=40°时,
∵ AB=AC,∠ACB =∠ABC =90°-α=70°
∵△BCD为等边三角形
∴∠BCD =60°
∴∠ACD = ∠ACB-∠BCD = 10°
22.
(1)证明:根据旋转图形的性质,可得△AEC≌△BFC,
∴∠FBC=∠EAC.
又∵∠ADC=∠BDP,∠EAC+∠ADC=180°-∠ACD=90°,
∴∠BDP+∠FBC=90°,
∴∠BPD=180°-(∠BDP+∠FBC)=90°,
∴AP⊥BE.
(2)证明:∵∠CEP=∠EPF=∠ECF=90°,
∴四边形CEPF是矩形.
∵CE=CF
∴四边形CEPF是正方形.
∴CE=EP=FP.
又∵∠CDE=∠BDP,CD=BD,∠CED=∠BPD=90°
∴△CED≌△BPD,
∴CE=BP.
∴EP+FP=2CE=2BP.
(3)成立.
理由如下:过点C作CG⊥AD,垂足为G,CH⊥BP,垂足为H.
∵△BFC由△AEC逆时针90°旋转得到,
∴∠AEC=∠BFC,CE=CF,∠ECF=90°.
∵∠CEG+∠AEC=180°,∠CFH+∠BFC=180°,
∴∠CEG=∠CFH.
∵∠CGE=∠CHF=90°,
∴△CEG≌△CFH,
∴CH=CG,EG=FH.
∴EP+FP=GP+HP
∵∠CGP=∠GPH=∠H=90°,
∴四边形CGPH是正方形.
又(2)可知,GP+PH=2BP,
∴EP+PF=2BP.
23.
解:(1)∵在四边形ABCD的转动过程中,BC、AD边的长度始终保持不变,BC=x,
∴在图2中,AC=BC AB=x 6,AD=AC+CD=x+9.
(2)∴位置二的图见图3.
(3)∵在四边形ABCD转动的过程中,BC、AD边的长度始终保持不变,
∴在图3中,BC=x,AC=AB+BC=6+x,AD=x+9,
∵图3中,△ACD为直角三角形,∠C=90°,
由勾股定理得:AC2+CD2=AD2,
∴(6+x)2+152=(x+9)2,
整理,得6x=180,
解得x=30,
即BC=30,
∴AD=39.
24. 解:(1)画图如图1所示;
(2)甲、乙、丙三名同学的发现都是正确的;
①甲发现正确;理由如下:
如图2所示,
延长CB到K,使BK=DE,连AK,
∵四边形ABCD是正方形,
∴AB=AD,∠ABF=∠ABK=∠ADE=90°,
在△AKB和△AED中,,
∴△AKB≌△AED(SAS),
∴∠BAK=∠DAE,
∵∠BAF+∠DAE=45°,
∴∠BAF+∠BAK=45°,
即∠KAF=45°,
∴∠KAF=∠FAE,
在△AKF和△AEF中,,
∴△AKF≌△AEF(SAS),
∴KF=EF,
又∵BK=DE,
∴EF=BF+DE;
②乙发现正确;理由如下:
延长CB到K,使BK=DE,连接AK,如图2所示:
同①得:△AKB≌△AED,
∴∠BAK=∠DAE,
∵∠BAF+∠DAE=45°,
∴∠BAF+∠BAK=45°,
即∠KAF=45°,
∴∠KAF=∠FAE,
在△AKF和△AEF中,,
∴△AKF≌△AEF(SAS),
∴KF=EF,
又∵BK=DE,
∴EF=BF+DE;
△CEF周长=CF+CE+EF
=CF+CE+(BF+DE)
=(CF+BF)+(CE+DE)
=BC+DC=2a(定值);
③丙发现正确;理由如下:
如图3,在AK上截取AG=AM,连接BG,GN,
在△ABG和△ADM中,,
∴△ABG≌△ADM(SAS),
∴BG=DM,∠ABG=∠ADB=45°,
又∵∠ABD=45°,
∴∠GBD=90°,
∵∠BAF+∠DAE=45°,
∴∠KAF=45°,
∴∠KAF=∠FAE,
在△GAN和△NAM中,,
∴△GAN≌△NAM(SAS),
∴NG=MN,
∵∠GBD=90°,
∴BG2+BN2=NG2,
∴BN2+DM2=MN2;
综上所述:甲、乙、丙三名同学的发现都是正确的.
25.
解:(1) ∵,
把绕点逆时针旋转至,
可使与重合,
三点共线,
则
即
在与中
故答案为:;
(2)当时,仍有,理由如下:
∵,
把绕点逆时针旋转至,可使与重合,如图,
三点共线,
在与中
即
故答案为:;
(3)猜想:,理由如下,
证明:将绕点顺时针旋转,得到,如图,连接,则
,
在中
在与中
.
26.
(1)证明:∵CO绕点C顺时针旋转60°得到CD,
∴CO=CD,∠OCD=60°,
∵△ABC是等边三角形,
∴CA=CB,∠BCA=60°,
∴∠BCA=∠OCD,
∴∠BCO=∠ACD,
在△BCO和△ACD中,
,
∴△BCO≌△ACD(SAS).
(2)解:∵CO=CD,∠OCD=60°,
∴△OCD是等边三角形,
∴OD=OC=6.∠ODC=60°,
∵△BCO≌△ACD,
∴AD=OB=8,∠BOC=∠ADC,
∵OA=10,
∴OA2=AD2+OD2,
∴∠ADO=90°,
∴∠ADC=∠ADO+∠CDO=150°,
∴∠BOC=∠ADC=150°.
,
同课章节目录
