九年级数学上册试题 3.2图形的旋转同步测试-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 3.2图形的旋转同步测试-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 00:00:00 | ||
图片预览

文档简介
3.2图形的旋转
一、单选题
1.如图,在平面直角坐标系中,A(﹣8,﹣1),B(﹣6,﹣9),C(﹣2.﹣9),D(﹣4,﹣1).先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )
A.(4,0) B.(5,0)
C.(4,0)或(﹣4,0) D.(5,0)或(﹣5,0)
2.如图,是正三角形内的一点,且,,.若将绕点逆时针旋转后,得到,则等于( ).
A.120° B.135° C.150° D.160°
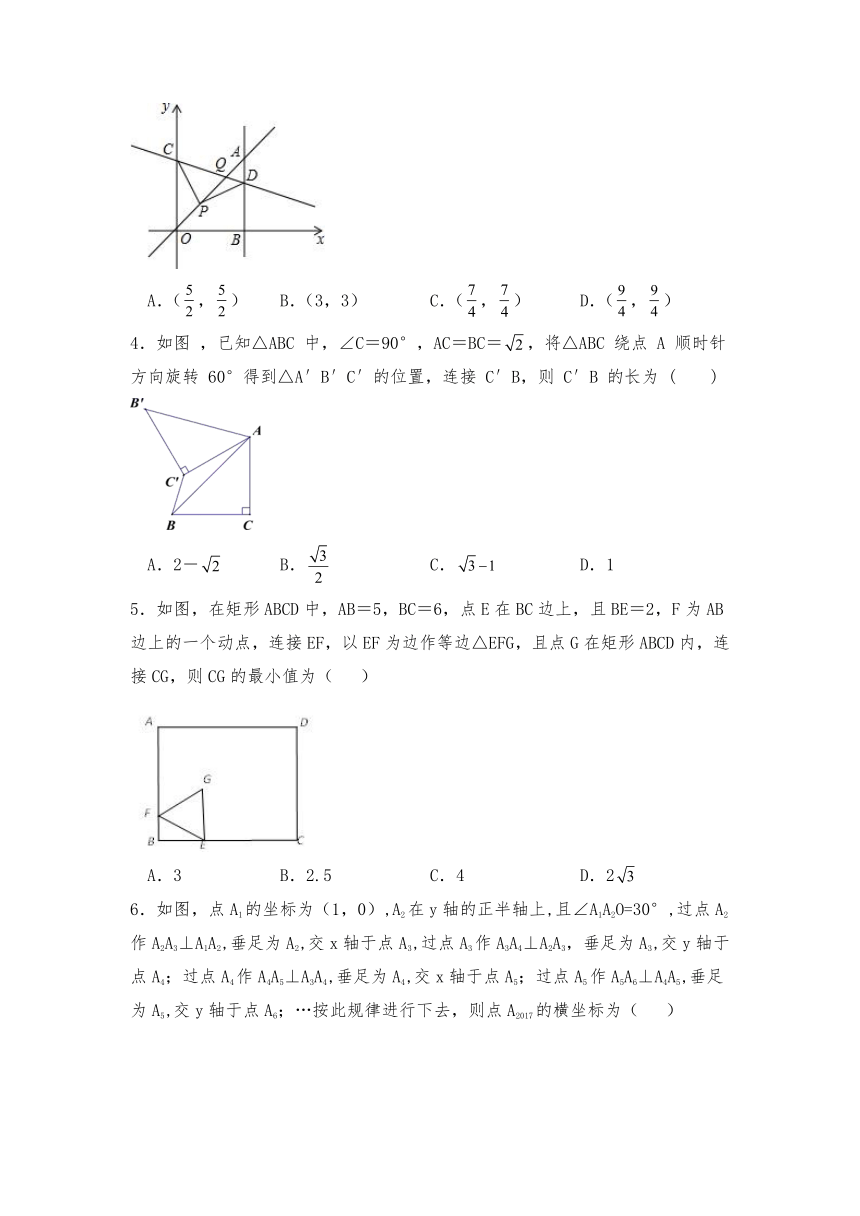
3.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
A.(,) B.(3,3) C.(,) D.(,)
4.如图 ,已知△ABC 中,∠C=90°,AC=BC=,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
A.2- B. C. D.1
5.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A.3 B.2.5 C.4 D.2
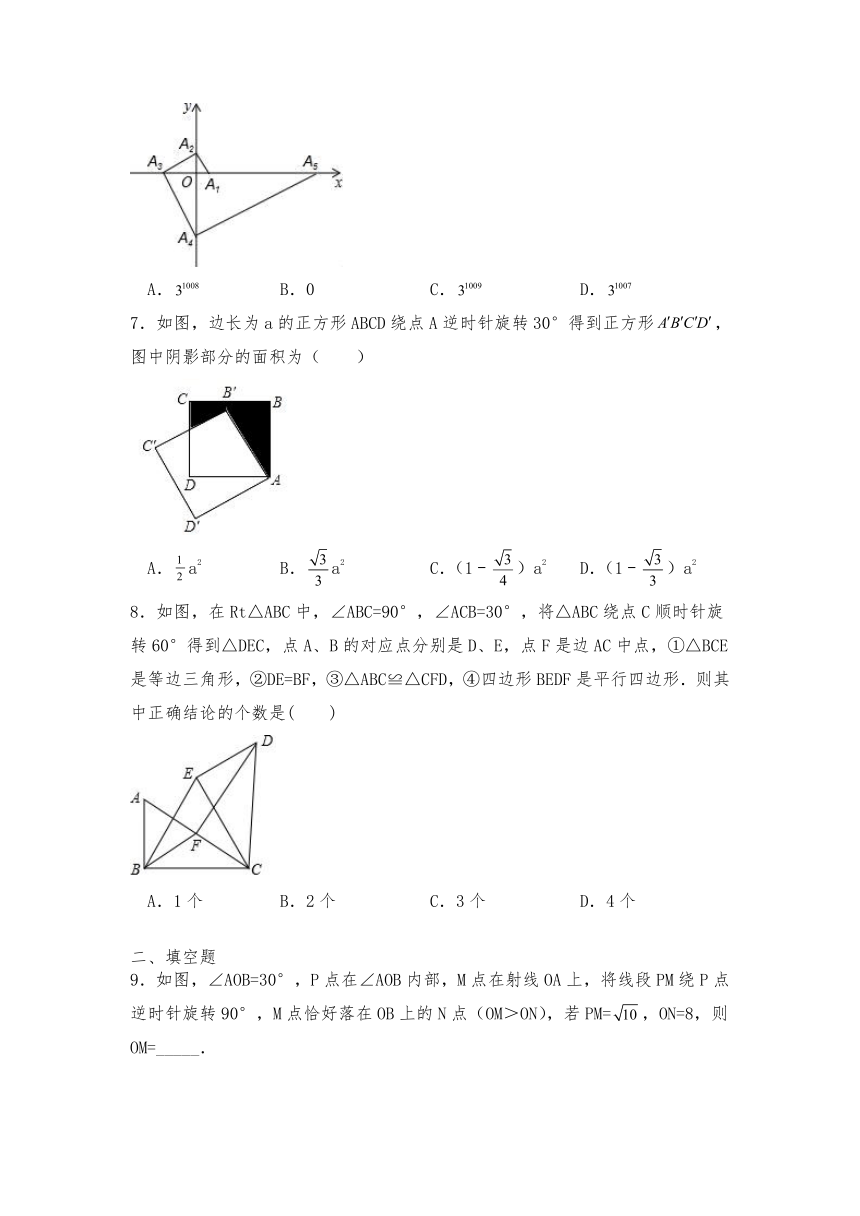
6.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为( )
A. B.0 C. D.
7.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形,图中阴影部分的面积为( )
A.a2 B.a2 C.(1﹣)a2 D.(1﹣)a2
8.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,①△BCE是等边三角形,②DE=BF,③△ABC≌△CFD,④四边形BEDF是平行四边形.则其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM=,ON=8,则OM=_____.
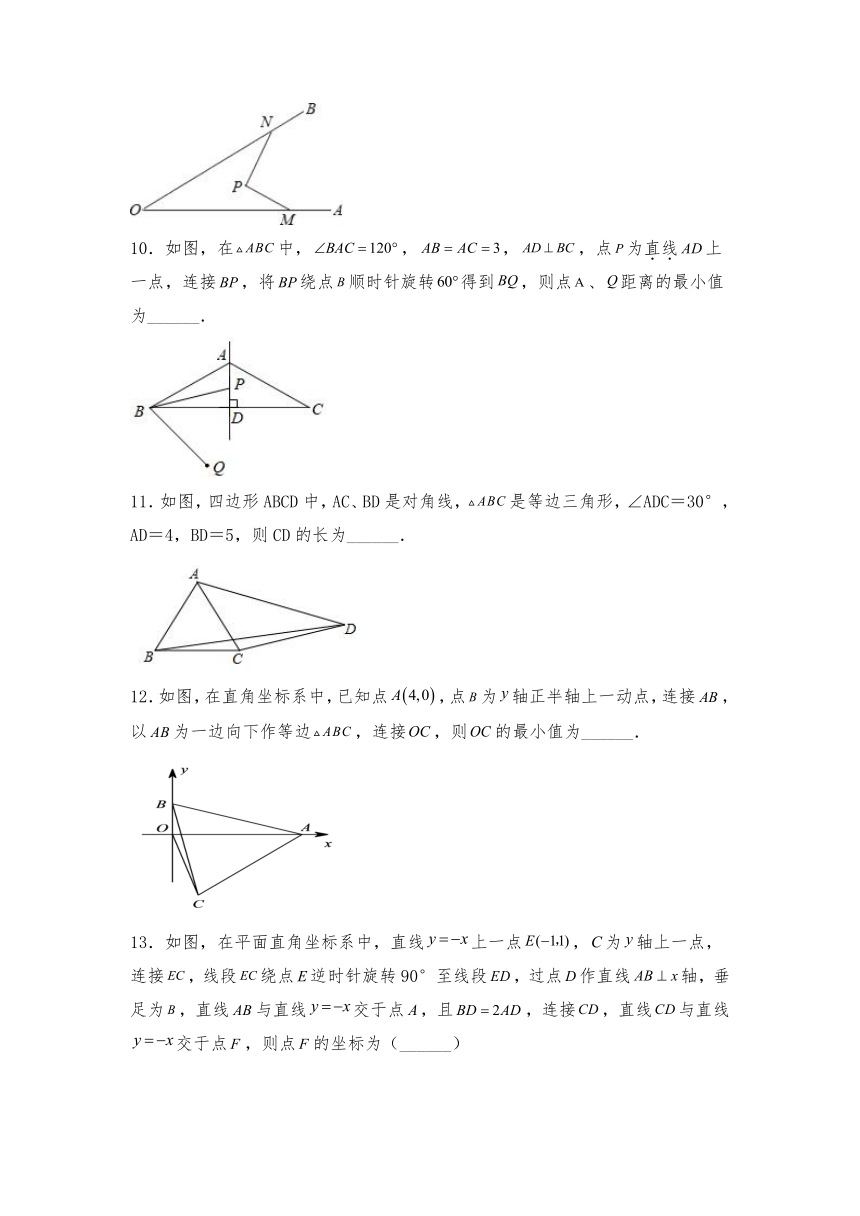
10.如图,在中,,,,点为直线上一点,连接,将绕点顺时针旋转得到,则点、距离的最小值为______.
11.如图,四边形ABCD中,AC、BD是对角线,是等边三角形,∠ADC=30°,AD=4,BD=5,则CD的长为______.
12.如图,在直角坐标系中,已知点,点为轴正半轴上一动点,连接,以为一边向下作等边,连接,则的最小值为______.
13.如图,在平面直角坐标系中,直线上一点,为轴上一点,连接,线段绕点逆时针旋转90°至线段,过点作直线轴,垂足为,直线与直线交于点,且,连接,直线与直线交于点,则点的坐标为(______)
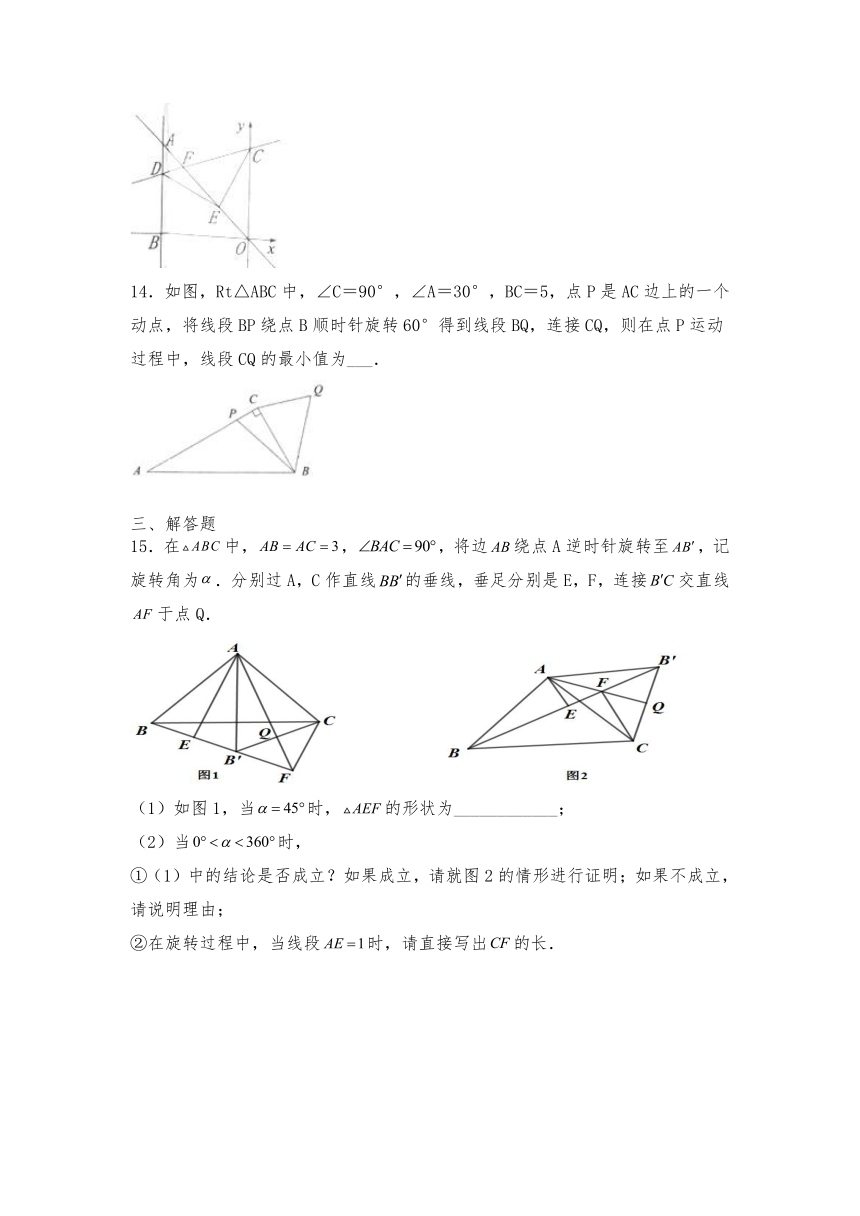
14.如图,Rt△ABC中,∠C=90°,∠A=30°,BC=5,点P是AC边上的一个动点,将线段BP绕点B顺时针旋转60°得到线段BQ,连接CQ,则在点P运动过程中,线段CQ的最小值为___.
三、解答题
15.在中,,,将边绕点A逆时针旋转至,记旋转角为.分别过A,C作直线的垂线,垂足分别是E,F,连接交直线于点Q.
(1)如图1,当时,的形状为____________;
(2)当时,
①(1)中的结论是否成立?如果成立,请就图2的情形进行证明;如果不成立,请说明理由;
②在旋转过程中,当线段时,请直接写出的长.
16.如图,在平面直角坐标系中,已知点A(1,0),将x轴绕点A顺时针旋转60°交y轴于点B,再将点B绕点A顺时针旋转90°得到点C.
(1)求直线BC的解析式;
(2)若点Q为平面直角坐标系中一点,且满足四边形ABCQ为平行四边形,求点Q的坐标;
(3)在直线BC和y轴上,是否分别存在点M和点N,使得以点M,N,A,C为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,说明理由.
17.(1)观察推理:如图1,中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:;
(2)类比探究:如图2,中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转 90°至,连接,求的面积;
(3)拓展提升:如图3,等边中,EC=BC=3cm,点O在BC上且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF,设点P运动的时间为t秒,当 秒时,,请说明理由.
18.如图所示,点A坐标为(0,a),点C坐标为(a,b),其中a、b满足+(b+3)2=0,将△ADC沿x轴正方向平移得到△BCE,其中四边形ABCD为长方形,∠ACD=70°.
(1)点E的坐标为 .
(2)在四边形ABCD中,点P从O点出发,以每秒1个单位长度的速度沿四边形ABCD顺时针运动(即O﹣A﹣B﹣C﹣D﹣A),运动时间为t秒(t>6),问当t为何值时,点P到x轴的距离为1?
(3)将△BCE以每秒10°绕点E顺时针旋转一周,当t= 时,△BCE的直角边(BC或CE)与AC平行.
19.如图,矩形ABCG与矩形CDEF全等,点B,C,D和点C,G,F分别在同一条直线上,其中AB=CD=4,BC=DE=8.连接对角线AC,CE.
(1)在图①中,连接AE,则AE= ;
(2)如图②,将图①中的矩形CDEF绕点C逆时针旋转,当CF平分∠ACE时,求此时点E到直线AC的距离.
(3)如图③,将图①中的矩形CDEF绕点C逆时针旋转到某一个位置,连接AE,连接DG并延长交AE于点M,取AG的中点N,连接MN,求MN长的最小值.
20.如图①②③,平面内三点O,M,N.如果将线段OM绕点O旋转90°得ON,称点N是点M关于点O的“等直点”,如果OM绕点O顺时针旋转90°得ON,称点N是点M关于点0的“正等直点”,如图②.
(1)如图2,在平面直角坐标系中,已知点P(2,1).
①在(-1,2),(2,-1),(1,-2)三点中, _________ 是点P关于原点O的“等直点”:
②若直线:交轴于点M,若点N是直线上一点,且点N是点M关于点P的“等直点”,求直线的解析式:
(2)如图3,已知点A的坐标为(2,0),点B在直线:上,若点B关于点A的“正等直点”C在坐标轴上,D是平面内一点,若四边形ABCD是平行四边形,直接写出点D的坐标.
21.如图,中,,,点在内,且,将绕点逆时针旋转90°得到,连接,,.
(1)试探究与的关系;
(2)当时,连接,求出的面积.
(3)请求出周长的最小值.
22.如图,在中,,,点,是边上两点,且,则线段,,之间有怎样的数量关系,并说明理由.
23.如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程的两个实数根.
(1)请尝试用根的判别式判定根的情况,并求出m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若∠BAC=30°,在(1)、(2)条件下求DC的长.
24.如图1,在中,,点D,E分别在边上,且,连接.现将绕点A顺时针方向旋转,旋转角为,如图2,连接.
(1)当时,求证:;
(2)如图3,当时,延长交于点,求证:垂直平分;
(3)在旋转过程中,求的面积的最大值,并写出此时旋转角的度数.
答案
一、单选题
D.C.D.C.CA.D.D.
二、填空题
9.4+2.
10.
11.3
12.2
13.(,).
14.
三、解答题
15.解:(1)由旋转性质得:,.
∵AE⊥,
∴.
∵AB=AC,∠ABC=∠ACB=45゜,
∴,
∵,AB=AC,,
∴.
∴.
∴.
∴.
∵CF⊥,
∴.
∴.
∵,
∴,且AF平分.
∴.
∴∠EAF=.
∵AE⊥,
∴∠EAF=∠EFA=45゜.
∴△AEF是等腰直角三角形.
故答案为:等腰直角三角形.
(2)①结论仍成立.
∵,,
∴.
∵,,
∴.
∴.
∵,
∴是等腰直角三角形.
∴.
又,
∴垂直平分.
∴,
∴.
∵,
∴是等腰直角三角形.
②如下图所示,当α<180゜时,
在直角△AEB中,由勾股定理得:,
∴.
∵△AEF是等腰直角三角形,是等腰直角三角形,
∴EF=AE=1,.
∵
∴
如下图所示,当180゜<α<360゜时,
在直角△AEB中,由勾股定理得:,
∴.
∵△AEF是等腰直角三角形,是等腰直角三角形,
∴EF=AE=1,.
∵,
∴.
综上所述,CF的长为或.
16.解:(1)轴绕点顺时针旋转交轴于点,
,
点,
,
,,
,
点绕点顺时针旋转得到点,
,,
过点作轴于点,
,
,,
,,
设直线的解析式为,
则有,
解得,
;
(2)设,
四边形为平行四边形,
、为平行四边形的对角线,
的中点,,的中点,,
,,
,,
,;
(3)在直线上,在轴上,
设,,,
①当、为平行四边形的对角线时,
中点的横坐标为,中点的横坐标为,
,
,
,;
②当、为平行四边形的对角线时,
中点的横坐标为,中点的横坐标为,
,
,
,;
③当、为平行四边形的对角线时,
中点的横坐标为,中点的横坐标为,
,
,
,;
综上所述:点的坐标为,或,或,.
17.(1) ∵BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
,
∴△AEC≌△CDB;
(2)如图,作B′D⊥AC于D,
∵斜边AB绕点A逆时针旋转90°至AB′,
∴AB′=AB,∠B′AB=90°,
即∠B′AC+∠BAC=90°,
而∠B+∠CAB=90°,
∴∠B=∠B′AC,
在△B′AD和△ABD中,
,
∴△B′AD≌△ABD,
∴B′D=AC=4,
∴△AB′C的面积=×4×4=8;
(3)由题意得:,则,
∵OF∥ED,
∴∠POF+∠OPC=180°,
∵∠POF=120°,
∴∠OPC=60°,
∵△BEC是等边三角形,
∴∠BCE=60°=∠OPC,
∴∠E=∠OPC=60°,
∴△COP是等边三角形,
∴PC=OC=2cm,
∴,解得,
即当t=1秒时,OF∥ED,
故答案为:1.
18.解:(1)∵+(b+3)2=0,
∴a-2=0,b+3=0,
∴a=2,b=-3,
∴点A坐标为(0,2),点C坐标为(2,-3),
∵四边形ABCD为长方形,
∴B(2,2),D(0,-3),
∴CD=2,
∵将△ADC沿x轴正方向平移得到△BCE,
∴CE=CD=2,
∴点E的坐标为(4,-3),
故答案为:(4,-3);
(2)∵点P到x轴的距离为1,
∴点P的坐标有(0,1),(2,1),(2,-1),(0,-1),
∵C长方形ABCD=AB+BC+CD+DA
=2+[2-(-3)] +2+[2-(-3)]
=14,
又∵点P从O点出发,以每秒1个单位长度的速度沿四边形ABCD顺时针运动(即O﹣A﹣B﹣C﹣D﹣A),运动时间为t秒(t>6),
∴点P的总路程为2+14=16,
∴t=16÷1=16,
∴6<t<16,
当点P从O点出发到(2,1)时,t=(2+2+1)÷1=5(不符合题意,舍去);
当点P从O点出发到(2,-1)时,t=(2+2+2+1)÷1=7(符合题意);
当点P从O点出发到(0,-1)时,t=(2+2+2+3+2+2)÷1=13(符合题意);
当点P从O点出发沿着O﹣A﹣B﹣C﹣D﹣O再到(0,1)时,
t=(14+1)÷5=15,
综上所述:当t的值为7或13或15时,点P到x轴的距离为1;
(3)①当BC与AC平行时,
∵∠ACD=70°,
∴∠DAC=∠ACB=20°,
将△BCE以每秒10°绕点E顺时针旋转一周,
BC转180°-20°=160°时满足,此时t=160°÷10°=16,
BC转360°-20°=340°时满足,此时t=340°÷10°=34,
②当CE与AC平行时,∠BEC=∠ACD=70°,
CE转70°时满足,此时t=70°÷10°=7,
BC转180°+70°=250°时满足,此时t=250°÷10°=25,
综上所述:当t=16或34或7或25时,△BCE的直角边(BC或CE)与AC平行.
19.解:(1)矩形与矩形全等,
,,
,
,
,
,
,
.
故答案为:;
(2)当平分时,
,由等腰三角形“三线合一”得:,,
设点到直线的距离为,
则由等面积法:,
,
此时点到直线的距离为;
(3)如图,过点作的平行线交的延长线于,连接,
,
,
,
,
,
,,
,
,
,
在与中,
,
,
,
的中点为,
,,
在矩形绕点逆时针旋转过程中的范围为:,
,
的最小值为,
的最小值为.
20.解:(1)如图2,连接OP,作PF⊥轴,将OP绕点O顺时针旋转90°得到OE,过点E作EH⊥轴,
∴PF=2,OF=1,∠PFO=∠EHO=90°,
∵将OP绕点O顺时针旋转90°得到OE,
∴OP=OE,∠POE=90°,
∴∠POF+∠EOH=90°,
∵∠POF+∠FPO=90°,
∴∠FPO=∠EOH,
又∵∠PFO=∠EHO=90°,OE=OP,
∴△PFO≌△OHE(AAS),
∴HE=OF=1,PF=OH=2,
∴点E(1,-2),
将OP绕点O顺时针旋转90°得到OG,
同理可求点G(-1,2),
∴,是点P关于原点O的“等直点”,
故答案为:,
②∵交轴于点M,
∴点M(0,4),
∵点N是点M关于点P的“等直点”,
∴MP=NP,MP⊥NP,
如图,当线段MP绕点P顺时针旋转90°得PN,过P作PQ⊥轴于点Q,NK⊥PQ交QP的延长线于点K,
则∠MQP=∠NKP=90°,
∠QMP+∠QPM=∠QPM+∠NPK=90°,
∴∠QMP=∠KPN,
∴△MPQ≌△PNK(AAS),
∴MQ=PK=4-1=3,PQ=NK=2,
∴点N(5,3),
∵点N是直线上一点,
∴
解得,
∴直线的解析式为:
当线段MP绕点P逆时针旋转90°得PN,
同理可得点N(-1,-1),
∴,
解得,
∴直线的解析式为:,
∴综上所述:直线的解析式为或
(2)如图3,当点C在轴上时,
∵点A的坐标为(2,0),
∴OA=2,
∵点C是点B关于点A的“正等直点”,
∴∠BAC=90°,AB=AC,
∴点B的横坐标为2,
∴点B的坐标(2,6),
∴AB=6=AC,
∴OC=8,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=6,
∴点D(8,-6);
若点C在轴上时,过点B作BE⊥轴于E,
∵点C是点B关于点A的“正等直点”,
∴∠BAC=90°,AB=AC,
∴∠BAE+∠CAO=90°,
又∵∠CAO+∠ACO=90°,
∴∠BAE=∠ACO,
又∵AC=AB,∠AOC=∠AEB=90°,
∴△ACO≌△ABE(AAS),
∴BE=AO=2,AE=OC,
∴点B的纵坐标为-2,
∴点B坐标为(,-2),
∴EO=,
∴CO=2+=,
∴点C(0,),
设点D(,),
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴
∴
∴点D(,),
综上所述:点D坐标为(8,-6)或(,).
21.(1)延长交于.
绕点逆时针旋转90°得到,
,,
,
,
又,,
,
,,
,
,
且,
(2),.
,
∵,
,,
当时,三点共线,与点重合.
,.
∴
由(1)知于,.
设,则
∴
∴(不合题意舍去)
∴
.
(3),,
∴BC=2,
由(1)知,,
∴当BD+BE最小时,△CBD周长最小;
,在以为圆心,为半径的圆上,
作AM⊥DE于M,交圆A于点,过点作圆的切线BQ,连接BD,连接EB并延长至H,使BH=BE,连接DH交BQ于K,
∵AD=AE,AM⊥DE
∴M是DE中点,
∵BH=BE,
∴B是HE中点,
∴BM是△DEH的中位线,
∴DH⊥DE,DH∥BM,
∵BQ是圆A的切线,
∴AB⊥BQ,
∴DE∥BQ,
∴K是DH中点,
∴点D、点H关于直线BQ对称,
∴点B是直线BQ上到点D、点E距离之和最小的点,
在圆A上任选异于点B的点P,连接PE、PD,PD交BQ于点N,
△PEN中,PE+PN﹥EN,
∴PE+PN+DN﹥EN+DN,
∴PE+PD﹥EN+DN,
前面已证,点B是直线BQ上到点D、点E距离之和最小的点,
∴EN+DN﹥DB+BE,
∴PE+PD﹥DB+BE,
∴点B是圆A上到点D、点E距离之和最小的点,
即DB+BE最小,此时△CBD周长最小;
,⊥DE,AD=AE,
,
又∵,
轴于.
作轴于
是矩形,
又∵
是正方形
,
∴EG=3-1=2,
由勾股定理得,,
周长的最小值
22.解:,,的数量关系为.
理由如下:如图,将绕点逆时针旋转至的位置,使与重合,连接,
则,,,.
又∵,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∴.
23.解:(1)、的长分别是关于的方程的两个实数根,
,即,
化简整理,得:,即.
又,
.
(2),理由如下:
由(1)得,当时,,
.
是的直径,
.
将绕点逆时针旋转后,得,如图所示.
,
,, .
,
,
点、、三点共线.
,
.
又,
为等腰直角三角形.
,
即.
(3)由(1)得,当时,
则有:,
∴可化为:
则
∴
.
,
,
∵,
∴,
由(2)得,,
∴
24.(1)根据题意:AB=AC,AD=AE,∠CAB=∠EAD=90,
∵∠CAE+∠BAE =∠BAD+∠BAE =90,
∴∠CAE=∠BAD,
在△ACE和△ABD中,,
∴△ACE△ABD(SAS),
∴CE=BD;
(2)根据题意:AB=AC,AD=AE,∠CAB=∠EAD=90,
在△ACE和△ABD中,,
∴△ACE△ABD(SAS),
∴∠ACE=∠ABD,
∵∠ACE+∠AEC=90,且∠AEC=∠FEB,
∴∠ABD+∠FEB=90,
∴∠EFB=90,
∴CF⊥BD,
∵AB=AC=,AD=AE=1,∠CAB=∠EAD=90,
∴BC=AB =,CD= AC+ AD=,
∴BC= CD,
∵CF⊥BD,
∴CF是线段BD的垂直平分线;
(3)中,边BC的长是定值,则BC边上的高取最大值时的面积有最大值,
∴当点D在线段BC的垂直平分线上时,的面积取得最大值,如图:
∵∵AB=AC=,AD=AE=1,∠CAB=∠EAD=90,DG⊥BC于G,
∴AG=BC=,∠GAB=45,
∴DG=AG+AD=,∠DAB=180-45=135,
∴的面积的最大值为:,
旋转角.
一、单选题
1.如图,在平面直角坐标系中,A(﹣8,﹣1),B(﹣6,﹣9),C(﹣2.﹣9),D(﹣4,﹣1).先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )
A.(4,0) B.(5,0)
C.(4,0)或(﹣4,0) D.(5,0)或(﹣5,0)
2.如图,是正三角形内的一点,且,,.若将绕点逆时针旋转后,得到,则等于( ).
A.120° B.135° C.150° D.160°
3.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
A.(,) B.(3,3) C.(,) D.(,)
4.如图 ,已知△ABC 中,∠C=90°,AC=BC=,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
A.2- B. C. D.1
5.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A.3 B.2.5 C.4 D.2
6.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为( )
A. B.0 C. D.
7.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形,图中阴影部分的面积为( )
A.a2 B.a2 C.(1﹣)a2 D.(1﹣)a2
8.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,①△BCE是等边三角形,②DE=BF,③△ABC≌△CFD,④四边形BEDF是平行四边形.则其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM=,ON=8,则OM=_____.
10.如图,在中,,,,点为直线上一点,连接,将绕点顺时针旋转得到,则点、距离的最小值为______.
11.如图,四边形ABCD中,AC、BD是对角线,是等边三角形,∠ADC=30°,AD=4,BD=5,则CD的长为______.
12.如图,在直角坐标系中,已知点,点为轴正半轴上一动点,连接,以为一边向下作等边,连接,则的最小值为______.
13.如图,在平面直角坐标系中,直线上一点,为轴上一点,连接,线段绕点逆时针旋转90°至线段,过点作直线轴,垂足为,直线与直线交于点,且,连接,直线与直线交于点,则点的坐标为(______)
14.如图,Rt△ABC中,∠C=90°,∠A=30°,BC=5,点P是AC边上的一个动点,将线段BP绕点B顺时针旋转60°得到线段BQ,连接CQ,则在点P运动过程中,线段CQ的最小值为___.
三、解答题
15.在中,,,将边绕点A逆时针旋转至,记旋转角为.分别过A,C作直线的垂线,垂足分别是E,F,连接交直线于点Q.
(1)如图1,当时,的形状为____________;
(2)当时,
①(1)中的结论是否成立?如果成立,请就图2的情形进行证明;如果不成立,请说明理由;
②在旋转过程中,当线段时,请直接写出的长.
16.如图,在平面直角坐标系中,已知点A(1,0),将x轴绕点A顺时针旋转60°交y轴于点B,再将点B绕点A顺时针旋转90°得到点C.
(1)求直线BC的解析式;
(2)若点Q为平面直角坐标系中一点,且满足四边形ABCQ为平行四边形,求点Q的坐标;
(3)在直线BC和y轴上,是否分别存在点M和点N,使得以点M,N,A,C为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,说明理由.
17.(1)观察推理:如图1,中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:;
(2)类比探究:如图2,中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转 90°至,连接,求的面积;
(3)拓展提升:如图3,等边中,EC=BC=3cm,点O在BC上且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF,设点P运动的时间为t秒,当 秒时,,请说明理由.
18.如图所示,点A坐标为(0,a),点C坐标为(a,b),其中a、b满足+(b+3)2=0,将△ADC沿x轴正方向平移得到△BCE,其中四边形ABCD为长方形,∠ACD=70°.
(1)点E的坐标为 .
(2)在四边形ABCD中,点P从O点出发,以每秒1个单位长度的速度沿四边形ABCD顺时针运动(即O﹣A﹣B﹣C﹣D﹣A),运动时间为t秒(t>6),问当t为何值时,点P到x轴的距离为1?
(3)将△BCE以每秒10°绕点E顺时针旋转一周,当t= 时,△BCE的直角边(BC或CE)与AC平行.
19.如图,矩形ABCG与矩形CDEF全等,点B,C,D和点C,G,F分别在同一条直线上,其中AB=CD=4,BC=DE=8.连接对角线AC,CE.
(1)在图①中,连接AE,则AE= ;
(2)如图②,将图①中的矩形CDEF绕点C逆时针旋转,当CF平分∠ACE时,求此时点E到直线AC的距离.
(3)如图③,将图①中的矩形CDEF绕点C逆时针旋转到某一个位置,连接AE,连接DG并延长交AE于点M,取AG的中点N,连接MN,求MN长的最小值.
20.如图①②③,平面内三点O,M,N.如果将线段OM绕点O旋转90°得ON,称点N是点M关于点O的“等直点”,如果OM绕点O顺时针旋转90°得ON,称点N是点M关于点0的“正等直点”,如图②.
(1)如图2,在平面直角坐标系中,已知点P(2,1).
①在(-1,2),(2,-1),(1,-2)三点中, _________ 是点P关于原点O的“等直点”:
②若直线:交轴于点M,若点N是直线上一点,且点N是点M关于点P的“等直点”,求直线的解析式:
(2)如图3,已知点A的坐标为(2,0),点B在直线:上,若点B关于点A的“正等直点”C在坐标轴上,D是平面内一点,若四边形ABCD是平行四边形,直接写出点D的坐标.
21.如图,中,,,点在内,且,将绕点逆时针旋转90°得到,连接,,.
(1)试探究与的关系;
(2)当时,连接,求出的面积.
(3)请求出周长的最小值.
22.如图,在中,,,点,是边上两点,且,则线段,,之间有怎样的数量关系,并说明理由.
23.如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程的两个实数根.
(1)请尝试用根的判别式判定根的情况,并求出m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若∠BAC=30°,在(1)、(2)条件下求DC的长.
24.如图1,在中,,点D,E分别在边上,且,连接.现将绕点A顺时针方向旋转,旋转角为,如图2,连接.
(1)当时,求证:;
(2)如图3,当时,延长交于点,求证:垂直平分;
(3)在旋转过程中,求的面积的最大值,并写出此时旋转角的度数.
答案
一、单选题
D.C.D.C.CA.D.D.
二、填空题
9.4+2.
10.
11.3
12.2
13.(,).
14.
三、解答题
15.解:(1)由旋转性质得:,.
∵AE⊥,
∴.
∵AB=AC,∠ABC=∠ACB=45゜,
∴,
∵,AB=AC,,
∴.
∴.
∴.
∴.
∵CF⊥,
∴.
∴.
∵,
∴,且AF平分.
∴.
∴∠EAF=.
∵AE⊥,
∴∠EAF=∠EFA=45゜.
∴△AEF是等腰直角三角形.
故答案为:等腰直角三角形.
(2)①结论仍成立.
∵,,
∴.
∵,,
∴.
∴.
∵,
∴是等腰直角三角形.
∴.
又,
∴垂直平分.
∴,
∴.
∵,
∴是等腰直角三角形.
②如下图所示,当α<180゜时,
在直角△AEB中,由勾股定理得:,
∴.
∵△AEF是等腰直角三角形,是等腰直角三角形,
∴EF=AE=1,.
∵
∴
如下图所示,当180゜<α<360゜时,
在直角△AEB中,由勾股定理得:,
∴.
∵△AEF是等腰直角三角形,是等腰直角三角形,
∴EF=AE=1,.
∵,
∴.
综上所述,CF的长为或.
16.解:(1)轴绕点顺时针旋转交轴于点,
,
点,
,
,,
,
点绕点顺时针旋转得到点,
,,
过点作轴于点,
,
,,
,,
设直线的解析式为,
则有,
解得,
;
(2)设,
四边形为平行四边形,
、为平行四边形的对角线,
的中点,,的中点,,
,,
,,
,;
(3)在直线上,在轴上,
设,,,
①当、为平行四边形的对角线时,
中点的横坐标为,中点的横坐标为,
,
,
,;
②当、为平行四边形的对角线时,
中点的横坐标为,中点的横坐标为,
,
,
,;
③当、为平行四边形的对角线时,
中点的横坐标为,中点的横坐标为,
,
,
,;
综上所述:点的坐标为,或,或,.
17.(1) ∵BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
,
∴△AEC≌△CDB;
(2)如图,作B′D⊥AC于D,
∵斜边AB绕点A逆时针旋转90°至AB′,
∴AB′=AB,∠B′AB=90°,
即∠B′AC+∠BAC=90°,
而∠B+∠CAB=90°,
∴∠B=∠B′AC,
在△B′AD和△ABD中,
,
∴△B′AD≌△ABD,
∴B′D=AC=4,
∴△AB′C的面积=×4×4=8;
(3)由题意得:,则,
∵OF∥ED,
∴∠POF+∠OPC=180°,
∵∠POF=120°,
∴∠OPC=60°,
∵△BEC是等边三角形,
∴∠BCE=60°=∠OPC,
∴∠E=∠OPC=60°,
∴△COP是等边三角形,
∴PC=OC=2cm,
∴,解得,
即当t=1秒时,OF∥ED,
故答案为:1.
18.解:(1)∵+(b+3)2=0,
∴a-2=0,b+3=0,
∴a=2,b=-3,
∴点A坐标为(0,2),点C坐标为(2,-3),
∵四边形ABCD为长方形,
∴B(2,2),D(0,-3),
∴CD=2,
∵将△ADC沿x轴正方向平移得到△BCE,
∴CE=CD=2,
∴点E的坐标为(4,-3),
故答案为:(4,-3);
(2)∵点P到x轴的距离为1,
∴点P的坐标有(0,1),(2,1),(2,-1),(0,-1),
∵C长方形ABCD=AB+BC+CD+DA
=2+[2-(-3)] +2+[2-(-3)]
=14,
又∵点P从O点出发,以每秒1个单位长度的速度沿四边形ABCD顺时针运动(即O﹣A﹣B﹣C﹣D﹣A),运动时间为t秒(t>6),
∴点P的总路程为2+14=16,
∴t=16÷1=16,
∴6<t<16,
当点P从O点出发到(2,1)时,t=(2+2+1)÷1=5(不符合题意,舍去);
当点P从O点出发到(2,-1)时,t=(2+2+2+1)÷1=7(符合题意);
当点P从O点出发到(0,-1)时,t=(2+2+2+3+2+2)÷1=13(符合题意);
当点P从O点出发沿着O﹣A﹣B﹣C﹣D﹣O再到(0,1)时,
t=(14+1)÷5=15,
综上所述:当t的值为7或13或15时,点P到x轴的距离为1;
(3)①当BC与AC平行时,
∵∠ACD=70°,
∴∠DAC=∠ACB=20°,
将△BCE以每秒10°绕点E顺时针旋转一周,
BC转180°-20°=160°时满足,此时t=160°÷10°=16,
BC转360°-20°=340°时满足,此时t=340°÷10°=34,
②当CE与AC平行时,∠BEC=∠ACD=70°,
CE转70°时满足,此时t=70°÷10°=7,
BC转180°+70°=250°时满足,此时t=250°÷10°=25,
综上所述:当t=16或34或7或25时,△BCE的直角边(BC或CE)与AC平行.
19.解:(1)矩形与矩形全等,
,,
,
,
,
,
,
.
故答案为:;
(2)当平分时,
,由等腰三角形“三线合一”得:,,
设点到直线的距离为,
则由等面积法:,
,
此时点到直线的距离为;
(3)如图,过点作的平行线交的延长线于,连接,
,
,
,
,
,
,,
,
,
,
在与中,
,
,
,
的中点为,
,,
在矩形绕点逆时针旋转过程中的范围为:,
,
的最小值为,
的最小值为.
20.解:(1)如图2,连接OP,作PF⊥轴,将OP绕点O顺时针旋转90°得到OE,过点E作EH⊥轴,
∴PF=2,OF=1,∠PFO=∠EHO=90°,
∵将OP绕点O顺时针旋转90°得到OE,
∴OP=OE,∠POE=90°,
∴∠POF+∠EOH=90°,
∵∠POF+∠FPO=90°,
∴∠FPO=∠EOH,
又∵∠PFO=∠EHO=90°,OE=OP,
∴△PFO≌△OHE(AAS),
∴HE=OF=1,PF=OH=2,
∴点E(1,-2),
将OP绕点O顺时针旋转90°得到OG,
同理可求点G(-1,2),
∴,是点P关于原点O的“等直点”,
故答案为:,
②∵交轴于点M,
∴点M(0,4),
∵点N是点M关于点P的“等直点”,
∴MP=NP,MP⊥NP,
如图,当线段MP绕点P顺时针旋转90°得PN,过P作PQ⊥轴于点Q,NK⊥PQ交QP的延长线于点K,
则∠MQP=∠NKP=90°,
∠QMP+∠QPM=∠QPM+∠NPK=90°,
∴∠QMP=∠KPN,
∴△MPQ≌△PNK(AAS),
∴MQ=PK=4-1=3,PQ=NK=2,
∴点N(5,3),
∵点N是直线上一点,
∴
解得,
∴直线的解析式为:
当线段MP绕点P逆时针旋转90°得PN,
同理可得点N(-1,-1),
∴,
解得,
∴直线的解析式为:,
∴综上所述:直线的解析式为或
(2)如图3,当点C在轴上时,
∵点A的坐标为(2,0),
∴OA=2,
∵点C是点B关于点A的“正等直点”,
∴∠BAC=90°,AB=AC,
∴点B的横坐标为2,
∴点B的坐标(2,6),
∴AB=6=AC,
∴OC=8,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=6,
∴点D(8,-6);
若点C在轴上时,过点B作BE⊥轴于E,
∵点C是点B关于点A的“正等直点”,
∴∠BAC=90°,AB=AC,
∴∠BAE+∠CAO=90°,
又∵∠CAO+∠ACO=90°,
∴∠BAE=∠ACO,
又∵AC=AB,∠AOC=∠AEB=90°,
∴△ACO≌△ABE(AAS),
∴BE=AO=2,AE=OC,
∴点B的纵坐标为-2,
∴点B坐标为(,-2),
∴EO=,
∴CO=2+=,
∴点C(0,),
设点D(,),
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴
∴
∴点D(,),
综上所述:点D坐标为(8,-6)或(,).
21.(1)延长交于.
绕点逆时针旋转90°得到,
,,
,
,
又,,
,
,,
,
,
且,
(2),.
,
∵,
,,
当时,三点共线,与点重合.
,.
∴
由(1)知于,.
设,则
∴
∴(不合题意舍去)
∴
.
(3),,
∴BC=2,
由(1)知,,
∴当BD+BE最小时,△CBD周长最小;
,在以为圆心,为半径的圆上,
作AM⊥DE于M,交圆A于点,过点作圆的切线BQ,连接BD,连接EB并延长至H,使BH=BE,连接DH交BQ于K,
∵AD=AE,AM⊥DE
∴M是DE中点,
∵BH=BE,
∴B是HE中点,
∴BM是△DEH的中位线,
∴DH⊥DE,DH∥BM,
∵BQ是圆A的切线,
∴AB⊥BQ,
∴DE∥BQ,
∴K是DH中点,
∴点D、点H关于直线BQ对称,
∴点B是直线BQ上到点D、点E距离之和最小的点,
在圆A上任选异于点B的点P,连接PE、PD,PD交BQ于点N,
△PEN中,PE+PN﹥EN,
∴PE+PN+DN﹥EN+DN,
∴PE+PD﹥EN+DN,
前面已证,点B是直线BQ上到点D、点E距离之和最小的点,
∴EN+DN﹥DB+BE,
∴PE+PD﹥DB+BE,
∴点B是圆A上到点D、点E距离之和最小的点,
即DB+BE最小,此时△CBD周长最小;
,⊥DE,AD=AE,
,
又∵,
轴于.
作轴于
是矩形,
又∵
是正方形
,
∴EG=3-1=2,
由勾股定理得,,
周长的最小值
22.解:,,的数量关系为.
理由如下:如图,将绕点逆时针旋转至的位置,使与重合,连接,
则,,,.
又∵,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∴.
23.解:(1)、的长分别是关于的方程的两个实数根,
,即,
化简整理,得:,即.
又,
.
(2),理由如下:
由(1)得,当时,,
.
是的直径,
.
将绕点逆时针旋转后,得,如图所示.
,
,, .
,
,
点、、三点共线.
,
.
又,
为等腰直角三角形.
,
即.
(3)由(1)得,当时,
则有:,
∴可化为:
则
∴
.
,
,
∵,
∴,
由(2)得,,
∴
24.(1)根据题意:AB=AC,AD=AE,∠CAB=∠EAD=90,
∵∠CAE+∠BAE =∠BAD+∠BAE =90,
∴∠CAE=∠BAD,
在△ACE和△ABD中,,
∴△ACE△ABD(SAS),
∴CE=BD;
(2)根据题意:AB=AC,AD=AE,∠CAB=∠EAD=90,
在△ACE和△ABD中,,
∴△ACE△ABD(SAS),
∴∠ACE=∠ABD,
∵∠ACE+∠AEC=90,且∠AEC=∠FEB,
∴∠ABD+∠FEB=90,
∴∠EFB=90,
∴CF⊥BD,
∵AB=AC=,AD=AE=1,∠CAB=∠EAD=90,
∴BC=AB =,CD= AC+ AD=,
∴BC= CD,
∵CF⊥BD,
∴CF是线段BD的垂直平分线;
(3)中,边BC的长是定值,则BC边上的高取最大值时的面积有最大值,
∴当点D在线段BC的垂直平分线上时,的面积取得最大值,如图:
∵∵AB=AC=,AD=AE=1,∠CAB=∠EAD=90,DG⊥BC于G,
∴AG=BC=,∠GAB=45,
∴DG=AG+AD=,∠DAB=180-45=135,
∴的面积的最大值为:,
旋转角.
同课章节目录
