九年级数学上册试题 4.1比例线段同步测试-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.1比例线段同步测试-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 963.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 22:55:58 | ||
图片预览



文档简介
4.1比例线段
一、单选题
1.已知实数a、b、c、d满足2 005a3=2 006b3=2 007c3=2 008d3,
=
则a-1+b-1+c-1+d-1的值为( ).
A.1 B.0 C.-1 D.±1
2.如图,在正方形中,点是对角线的中点,是线段上的动点(不与点,重合),交于点,于点.则对于下列结论:①;②;③;④,其中错误结论的个数是( )
A.0 B.1 C.2 D.3
3.已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )
A. B. C. D.
4.若线段a=6 cm,b=3 cm,且c是a,b的比例中项,则线段c的长度为( )
A.3 cm B.±3 cm C.±18 cm D.18 cm
5.如图,线段,点是线段的黄金分割点(),点是线段的黄金分割点(),点是线段的黄金分割点(),..,依此类推,则线段的长度是( )
A. B. C. D.
6.在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动;同时,动点Q从点B出发沿BC力向以每秒1cm的速度向终点C运动,将△PQC翻折,点P的对应点为R,设点Q运动的时间为t秒,若四边形PCRQ为菱形,则t的值为( )
A. B.2 C.1 D.
7.下列说法正确的个数有( )
①垂线段最短;
②一对内错角的角平分线互相平行;
③平面内的n条直线最多有个交点;
④若,则;
⑤平行于同一直线的两条直线互相平行,垂直于同一直线的两条直线也互相平行.
A.1个 B.2个 C.3个 D.4个
8.,,为非零实数,且,若,则等于( ).
A.8 B.4 C.2 D.1
二、填空题
9.已知且则a的值为_______.
10.在平面直角坐标系中,关于的一次函数,其中常数k满足,常数b满足b>0且b是2和8的比例中项,则该一次函数的解析式为______.
11.春节临近,各种新鲜水果大量上市.某商人根据市场调查,购进草莓和车厘子两种水果,已知销售每斤草莓的利润率为,每斤车厘子的利润率为.当售出的草莓和车厘子的数量之比为时,商人得到的总利润率为.要使商人得到的总利润率为,那么售出的草莓和车厘子的数量之比为_________.
12.若,且,则的值为_________.
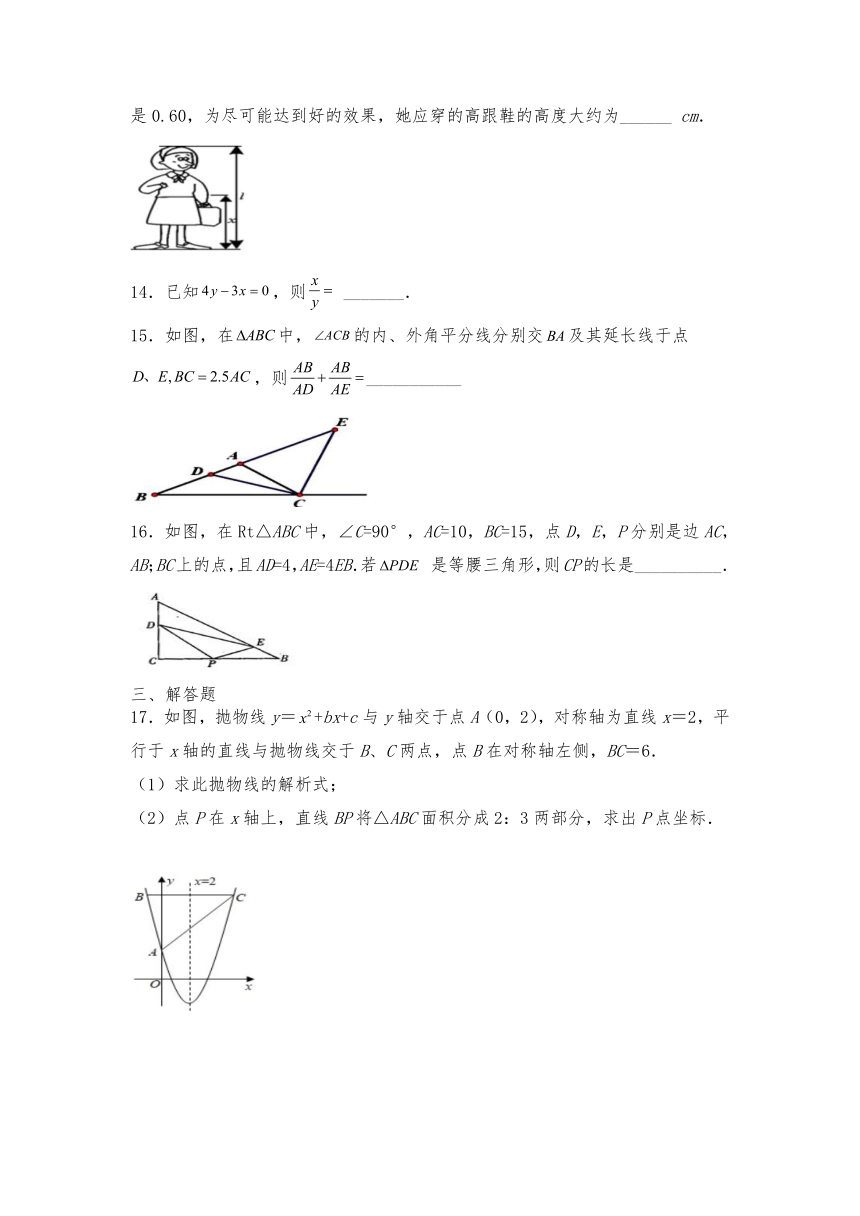
13.美是一种感觉,当人体下半身身长与身高的比值越接近(约为0.618)时,越给人一种美感.如图,某女士身高165cm,下半身身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为______ cm.
14.已知,则 _______.
15.如图,在中,的内、外角平分线分别交及其延长线于点,则___________
16.如图,在Rt△ABC中,∠C=90°,AC=10,BC=15,点D,E,P分别是边AC,AB;BC上的点,且AD=4,AE=4EB.若 是等腰三角形,则CP的长是__________.
三、解答题
17.如图,抛物线y=+bx+c与y轴交于点A(0,2),对称轴为直线x=2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)求此抛物线的解析式;
(2)点P在x轴上,直线BP将△ABC面积分成2:3两部分,求出P点坐标.
18.作出线段的黄金分割点(不写作法,保留作图痕迹)
19.如图,点A坐标是(0,0),点C坐标是(2,2),现有E、F两点分别从点D(0,2)和点B(2,0)向下和向右以每秒一个单位速度移动,Q为EF中点.设运动时间为t.
(1)在运动过程中始终与线段EC相等的线段是 ;四边形CEAF面积= .
(2)当t=1秒时,求线段CQ的长.
(3)过点B作BP平行于CF交EC于点P.当t= 时,线段AP最短,此时作直线EP与x轴交于点K,试证明,点K是线段AB的黄金分割点.
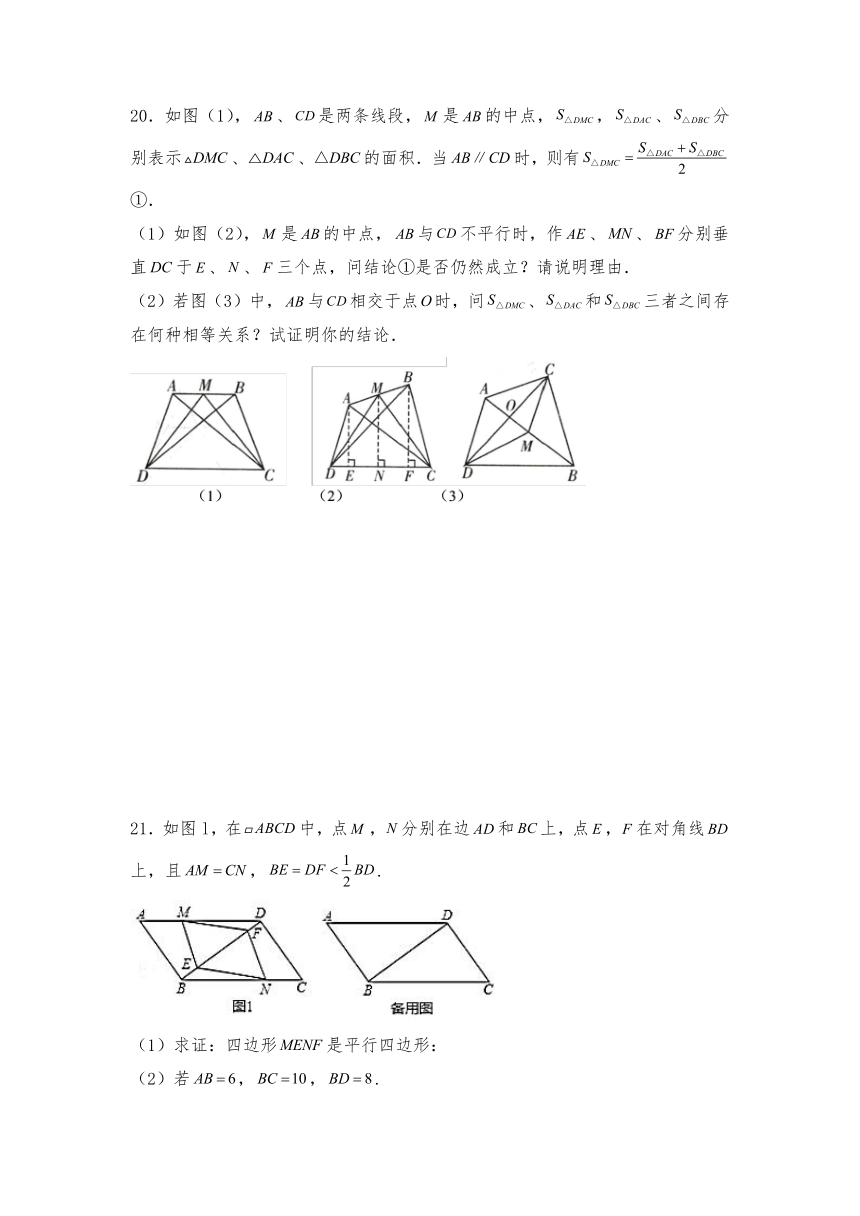
20.如图(1),、是两条线段,是的中点,,、分别表示、、的面积.当时,则有 ①.
(1)如图(2),是的中点,与不平行时,作、、分别垂直于、、三个点,问结论①是否仍然成立?请说明理由.
(2)若图(3)中,与相交于点时,问、和三者之间存在何种相等关系?试证明你的结论.
21.如图l,在中,点,分别在边和上,点,在对角线上,且,.
(1)求证:四边形是平行四边形:
(2)若,,.
①当四边形是菱形时,的长为______;
②当四边形是正方形时,的长为______;
③当四边形是矩形且时,的长为______.
22.材料一:“黄金分割比”的定义如下:
“如图,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,=叫做黄金比.”根据定义不难发现,在线段AB另有一点D把线段AB分成两条线段AD和BD,满足=,所以点D也是线段AB的黄金分割点.
材料二:对于实数:a1<a2<a3<a4,如果满足(a3﹣a1)2=(a4﹣a3)(a4﹣a1),(a4﹣a2)2=(a2﹣a1)(a4﹣a1)则称a3为a1,a4的黄金数,a2为a1,a4的白银数.
请根据以上材料,回答下列问题
(1)如图,若AB=4,点C和点D是线段AB的黄金分割点,则AC= ,CD= .
(2)实数0<a<b<1,且b为0,1的黄金数,a为0,1的白银数,求b﹣a的值.
(3)实数k<n<m<t,t=2|k|,m,n分别为k,t的黄金数和白银数,求的值.
23.在△ABC中,AB=AC=6,∠BAC=90°,AD⊥BC于点D,E为线段AD上的一点,AE:DE=2:1,以AE为直角边在直线AD右侧构造等腰Rt△AEF,使∠EAF=90°,连接CE,G为CE的中点.
(1)如图1,EF与AC交于点H,连接GH,求线段GH的长度.
(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α且45°<α<135°,H为线段EF的中点,连接DG,HG,猜想∠DGH的大小是否为定值,并证明你的结论;
(3)如图3,连接BG,将△AEF绕点A逆时针旋转,在旋转过程中,请直接写出BG长度的最大值.
24.已知,求的值.
25.已知,在△ABC中,AB=AC,在射线AB上截取线段BD,在射线CA上截取线段CE,连结DE,DE所在直线交直线BC于点M.
猜想:当点D在边AB的延长线上,点E在边AC上时,过点E作EF∥AB交BC于点F,如图①.若BD=CE,则线段DM、EM的大小关系为 .
探究:当点D在边AB的延长线上,点E在边CA的延长线上时,如图②.若BD=CE,判断线段DM、EM的大小关系,并加以证明.
拓展:当点D在边AB上(点D不与A、B重合),点E在边CA的延长线上时,如图③.若BD=1,CE=4,DM=0.7,求EM的长.
26.如图一,矩形中,,,是上一点,将沿折叠,使点落在上一点处,连结、.
求的长度;
设点、、分别在线段、、上,当且四边形为矩形时,请说明矩形的长宽比为,并求的长.(如图二)
答案
一、单选题
D.B.B.A.AC.B.A
二、填空题
9.8;
10.或.
11..
12.19.
13.8
14..
15.5.
16. 或
三、解答题
17.
解:(1)由题意得:x=﹣=﹣=2,c=2,
解得:b=﹣4,c=2,
∴抛物线的解析式为y=﹣4x+2;
(2)∵抛物线对称轴为直线x=2,BC=6,
∴,
解得,
把x=5代入抛物线解析式y=﹣4x+2,得:y=﹣4×5+2=7,
∴B(﹣1,7),C(5,7),
设直线AC解析式为y=kx+2,把C(5,7)代入得:7=5k+2,
∴k=1,
∴直线AC解析式为y=x+2,
作直线BP,与AC交于点D,过D作DE⊥x轴,垂足为E,过C作CF⊥x轴,垂足为F,过A作AQ⊥CF,垂足为Q,交DE于点G,
则四边形AOEG是矩形,四边形OFQA是矩形,四边形GEFQ是矩形,DG∥CQ,
∵C(5,7),
∴OF=AQ=5,OE=AG=;
∵直线BP将△ABC面积分成2:3两部分,根据同高两个三角形的面积比等于对应底之比,得AD:DC=2:3或AD:DC=3:2即AD:AC=2:5或AD:AC=3:5,
∵DG∥CQ,
∴,
∴或,
∴=2或=3,
当=2时,y=x+2=4,
当=3时,y=x+2=5,
∴点D的坐标为(2,4)或(3,5),
当点D的坐标为(2,4)时,设直线BP的解析式为y=mx+n,
根据题意,得,
解得,
∴直线BP的解析式为y=-x+6,
当y=0时,-x+6=0,解得x=6,
∴点P的坐标为(6,0);
当点D的坐标为(3,5)时,设直线BP的解析式为y=hx+t,
根据题意,得,
解得,
∴直线BP的解析式为y=x+,
当y=0时,x+=0,解得x=13,
∴点P的坐标为(13,0);
综上所述,P的坐标为(6,0)或(13,0).
18.
解:如图,点即为所求.
19.
解:(1)连接CD、CB,如图1所示:
∵A(0,0)、C(2,2)、D(0,2)、B(2,0),
∴CD=CB=AB=AD=2,
∴四边形DABC是菱形
又
∴四边形ABCD是正方形,
∵E、F两点分别从点D和点B向下和向右以每秒一个单位速度移动,
∴DE=BF,
∵∠CDE=∠CBF=90°,
∴△CDE≌△CBF(SAS),
∴EC=FC,
S四边形CEAF=S四边形CEAB+S△CBF=S四边形CEAB+S△CDE=S正方形ABCD=CB CD=2×2=4,
故答案为:FC,4;
(2)∵△CDE≌△CBF,
∴EC=FC,∠DCE=∠BCF,
∵∠DCE+∠ECB=90°,
∴∠BCF+∠ECB=90°,即∠ECF=90°,
∴△ECF是等腰直角三角形,
当t=1时,DE=1,
在Rt△CDE中,由勾股定理得:CE===,
∴EF=CE=×=,
∵Q为EF中点,
∴CQ=EF==;
(3)∵BP∥CF,∠ECF=90°,
∴∠BPC=90°,
∴点P的轨迹在以BC为直径的圆弧上,
设BC的中点为G,连接AG,如图2所示:
当点P在AG上时,AP最短,
此时,PG=BG=1,
在Rt△ABG中,由勾股定理得AG===,
∴AP=AG﹣PG=﹣1,
∵BC∥DE,
∴∠AEP=∠GCP,
∵GC=GP,
∴∠GCP=∠GPC,
∵∠GPC=∠APE,
∴∠AEP=∠APE,
∴AP=AE=﹣1,
∴E(0,1﹣),
∴DE=2﹣(1﹣)=+1,
∴t=(+1)s,
故答案为:(+1)s;
设CE的解析式为:y=kx+b(k≠0),
将C(2,2)、E(0,1﹣)代入解析式得:,
解得:,
∴CE的解析式为:y=x+1﹣,
令y=0,x=3﹣,
∴K(3﹣,0),
∴BK=2﹣(3﹣)=﹣1,
∴=,
∴点K是线段AB的黄金分割点.
20.
(1)当和不平行时,结论①仍然成立.
如图,由已知,可得,和两两平行,
∴四边形是梯形.
∴为的中点,
∴是梯形的中位线.
∴.
∴.
∴.
(2)∵为的中点,
∴,.
∴
.
∴.
∴.
21.
(1)证明:如图1中,设的中点为.连接,,,.
四边形是平行四边形,
与互相平分且交于点,,
,
四边形是平行四边形,
与互相平分且交于点,
,,
,
,
四边形是平行四边形.
(2)①如图中,连接交于点,当时,四边形是菱形.
,,,
,
,
,
,
,
.
②在①的基础上,满足时,四边形是正方形,
易知,
,
,
.
③如图中,连接交于点,作于.
,
,
,,
,
,
当时,四边形是矩形,
.
故答案为:5,1,.
22.
解:(1)∵AB=4,点C和点D是线段AB的黄金分割点,
∴AC=BD=AB=×4=2﹣2,
∴DC=AC+BD﹣AB=2(2﹣2)﹣4=4﹣8;
故答案为:2﹣2,4﹣8;
(2)∵b为0,1的黄金数,且实数0<b<1,
∴(b﹣0)2=(1﹣b)(1﹣0),
b2+b﹣1=0,
b1=<0(舍),b2=>0,
∵a为0,1的白银数,且实数0<a<1,
∴(1﹣a)2=(a﹣0)(1﹣0),
a2﹣3a+1=0,
a1=>1(舍),a2=<1,
∴b﹣a=﹣=﹣2;
(3)∵m,n分别为k,t的黄金数和白银数,实数k<n<m<t,
∴
分两种情况:
i)当k≥0时,t=2k,
由①得:(m﹣k)2=(2k﹣m)(2k﹣k),
m2﹣km﹣k2=0,
m=k;
由②得:(2k﹣n)2=(n﹣k)(2k﹣k),
n2﹣5kn+5k2=0,
n=k,
∵k<n<m<t,
∴m=k,n=k
∴===;
ii)当k<0时,t=﹣2k,
由①得:(m﹣k)2=(﹣2k﹣m)(﹣2k﹣k),
m2﹣5km﹣5k2=0,
m=k;
由②得:(﹣2k﹣n)2=(n﹣k)(﹣2k﹣k),
n2+7kn+k2=0,
n=k>0,
∵k<n<m<t,
∴m>0,
∴m=k,n=k,
∴ ===;
综上,的值是或.
23.
解:(1)如图1中,连接BE,CF.
∵AB=AC=6,∠BAC=90°,AD⊥BC于点D,
∴BC==12,BD=CD=6,
∴AD=BD=DC=6,
∴∠DAB=∠DAC=45°,
∵△AEF是等腰直角三角形,
∴AE=AF
∵∠DAH=45°,
∴∠FAH=90°-∠DAH=45°,
∴EH=HF,
∵AE:DE=2:1,AE+DE=6,
∴AE=4,DE=2,
∴BE=,
∵AB=AC,AE=AF,∠BAC=∠EAF=90°,
∴∠BAC-∠CAE=∠EAF-∠CAE,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(SAS),
∴CF=BE=2,
∵EG=CG,EH=FH,
∴GH=CF=.
(2)结论:∠DGH=90°是定值.
理由:连接BE,CF,设CF交BE于点O,BE交AC于J.
∵AB=AC,AE=AF,∠BAC=∠EAF=90°,
∴∠BAC+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(SAS),
∴∠ABE=∠ACF,
∵∠AJB=∠CJO,
∴∠COJ=∠BAJ=90°,
∴CF⊥BE,
∵EH=HF,EG=GC,
∴GH∥CF,
∵CD=DB,CG=GE,
∴DG∥BE,
∴DG⊥GH,
∴∠DGH=90°.
(3)如图3中,取AC的中点J,连接BJ,JG.
由题意AJ=JC=3,AB=6,
∵∠BAJ=90°,
∴BJ==3,
∵AJ=JC,EG=CG,
∴JG=AE=2,
∵BG≤BJ+JG,
∴BG≤3+2,
∴BG的最大值为3+2.
24.
因为,
所以a=b,c=d,e=f,
所以.
25.
(1)如图1中,猜想:DM=EM.
理由:作EF∥AB交BC于F,
∵AB=AC,
∴∠ABC=∠C,
∵EF∥AD,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
,
∴△BDM≌△FEM,
∴DM=EM.
故答案为DM=EM.
(2)结论DM=EM.
理由:如图2中,作EF∥AB交CB的延长线于F,
∵AB=AC,
∴∠ABC=∠C,
∵EF∥AB,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
,
∴△BDM≌△FEM,
∴DM=EM.
(3)如图3中,作EF∥AB交CB的延长线于F,
∵EF∥AB,
∴∠F=∠ABC,
∵AB=AC,
∴∠ABC=∠C,
∴∠F=∠C,
∴EF=CE=4,
∵BD∥EF,
∴,
∴,
∴EM=2.8,
故答案为2.8.
26.
解:(1如图一,在矩形中,,,,
由折叠可得:,,
∴直角三角形中,,
∴,
设,则,
在中,,
解得,
即;
(2)如图二,当,且四边形为矩形时,点在的垂直平分线上,
即垂直平分,
∴,①
又∵,
∴,
∵,
∴,即
解得,②
∴由①②得:矩形的长宽比为,
在中,.
一、单选题
1.已知实数a、b、c、d满足2 005a3=2 006b3=2 007c3=2 008d3,
=
则a-1+b-1+c-1+d-1的值为( ).
A.1 B.0 C.-1 D.±1
2.如图,在正方形中,点是对角线的中点,是线段上的动点(不与点,重合),交于点,于点.则对于下列结论:①;②;③;④,其中错误结论的个数是( )
A.0 B.1 C.2 D.3
3.已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )
A. B. C. D.
4.若线段a=6 cm,b=3 cm,且c是a,b的比例中项,则线段c的长度为( )
A.3 cm B.±3 cm C.±18 cm D.18 cm
5.如图,线段,点是线段的黄金分割点(),点是线段的黄金分割点(),点是线段的黄金分割点(),..,依此类推,则线段的长度是( )
A. B. C. D.
6.在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动;同时,动点Q从点B出发沿BC力向以每秒1cm的速度向终点C运动,将△PQC翻折,点P的对应点为R,设点Q运动的时间为t秒,若四边形PCRQ为菱形,则t的值为( )
A. B.2 C.1 D.
7.下列说法正确的个数有( )
①垂线段最短;
②一对内错角的角平分线互相平行;
③平面内的n条直线最多有个交点;
④若,则;
⑤平行于同一直线的两条直线互相平行,垂直于同一直线的两条直线也互相平行.
A.1个 B.2个 C.3个 D.4个
8.,,为非零实数,且,若,则等于( ).
A.8 B.4 C.2 D.1
二、填空题
9.已知且则a的值为_______.
10.在平面直角坐标系中,关于的一次函数,其中常数k满足,常数b满足b>0且b是2和8的比例中项,则该一次函数的解析式为______.
11.春节临近,各种新鲜水果大量上市.某商人根据市场调查,购进草莓和车厘子两种水果,已知销售每斤草莓的利润率为,每斤车厘子的利润率为.当售出的草莓和车厘子的数量之比为时,商人得到的总利润率为.要使商人得到的总利润率为,那么售出的草莓和车厘子的数量之比为_________.
12.若,且,则的值为_________.
13.美是一种感觉,当人体下半身身长与身高的比值越接近(约为0.618)时,越给人一种美感.如图,某女士身高165cm,下半身身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为______ cm.
14.已知,则 _______.
15.如图,在中,的内、外角平分线分别交及其延长线于点,则___________
16.如图,在Rt△ABC中,∠C=90°,AC=10,BC=15,点D,E,P分别是边AC,AB;BC上的点,且AD=4,AE=4EB.若 是等腰三角形,则CP的长是__________.
三、解答题
17.如图,抛物线y=+bx+c与y轴交于点A(0,2),对称轴为直线x=2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)求此抛物线的解析式;
(2)点P在x轴上,直线BP将△ABC面积分成2:3两部分,求出P点坐标.
18.作出线段的黄金分割点(不写作法,保留作图痕迹)
19.如图,点A坐标是(0,0),点C坐标是(2,2),现有E、F两点分别从点D(0,2)和点B(2,0)向下和向右以每秒一个单位速度移动,Q为EF中点.设运动时间为t.
(1)在运动过程中始终与线段EC相等的线段是 ;四边形CEAF面积= .
(2)当t=1秒时,求线段CQ的长.
(3)过点B作BP平行于CF交EC于点P.当t= 时,线段AP最短,此时作直线EP与x轴交于点K,试证明,点K是线段AB的黄金分割点.
20.如图(1),、是两条线段,是的中点,,、分别表示、、的面积.当时,则有 ①.
(1)如图(2),是的中点,与不平行时,作、、分别垂直于、、三个点,问结论①是否仍然成立?请说明理由.
(2)若图(3)中,与相交于点时,问、和三者之间存在何种相等关系?试证明你的结论.
21.如图l,在中,点,分别在边和上,点,在对角线上,且,.
(1)求证:四边形是平行四边形:
(2)若,,.
①当四边形是菱形时,的长为______;
②当四边形是正方形时,的长为______;
③当四边形是矩形且时,的长为______.
22.材料一:“黄金分割比”的定义如下:
“如图,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,=叫做黄金比.”根据定义不难发现,在线段AB另有一点D把线段AB分成两条线段AD和BD,满足=,所以点D也是线段AB的黄金分割点.
材料二:对于实数:a1<a2<a3<a4,如果满足(a3﹣a1)2=(a4﹣a3)(a4﹣a1),(a4﹣a2)2=(a2﹣a1)(a4﹣a1)则称a3为a1,a4的黄金数,a2为a1,a4的白银数.
请根据以上材料,回答下列问题
(1)如图,若AB=4,点C和点D是线段AB的黄金分割点,则AC= ,CD= .
(2)实数0<a<b<1,且b为0,1的黄金数,a为0,1的白银数,求b﹣a的值.
(3)实数k<n<m<t,t=2|k|,m,n分别为k,t的黄金数和白银数,求的值.
23.在△ABC中,AB=AC=6,∠BAC=90°,AD⊥BC于点D,E为线段AD上的一点,AE:DE=2:1,以AE为直角边在直线AD右侧构造等腰Rt△AEF,使∠EAF=90°,连接CE,G为CE的中点.
(1)如图1,EF与AC交于点H,连接GH,求线段GH的长度.
(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α且45°<α<135°,H为线段EF的中点,连接DG,HG,猜想∠DGH的大小是否为定值,并证明你的结论;
(3)如图3,连接BG,将△AEF绕点A逆时针旋转,在旋转过程中,请直接写出BG长度的最大值.
24.已知,求的值.
25.已知,在△ABC中,AB=AC,在射线AB上截取线段BD,在射线CA上截取线段CE,连结DE,DE所在直线交直线BC于点M.
猜想:当点D在边AB的延长线上,点E在边AC上时,过点E作EF∥AB交BC于点F,如图①.若BD=CE,则线段DM、EM的大小关系为 .
探究:当点D在边AB的延长线上,点E在边CA的延长线上时,如图②.若BD=CE,判断线段DM、EM的大小关系,并加以证明.
拓展:当点D在边AB上(点D不与A、B重合),点E在边CA的延长线上时,如图③.若BD=1,CE=4,DM=0.7,求EM的长.
26.如图一,矩形中,,,是上一点,将沿折叠,使点落在上一点处,连结、.
求的长度;
设点、、分别在线段、、上,当且四边形为矩形时,请说明矩形的长宽比为,并求的长.(如图二)
答案
一、单选题
D.B.B.A.AC.B.A
二、填空题
9.8;
10.或.
11..
12.19.
13.8
14..
15.5.
16. 或
三、解答题
17.
解:(1)由题意得:x=﹣=﹣=2,c=2,
解得:b=﹣4,c=2,
∴抛物线的解析式为y=﹣4x+2;
(2)∵抛物线对称轴为直线x=2,BC=6,
∴,
解得,
把x=5代入抛物线解析式y=﹣4x+2,得:y=﹣4×5+2=7,
∴B(﹣1,7),C(5,7),
设直线AC解析式为y=kx+2,把C(5,7)代入得:7=5k+2,
∴k=1,
∴直线AC解析式为y=x+2,
作直线BP,与AC交于点D,过D作DE⊥x轴,垂足为E,过C作CF⊥x轴,垂足为F,过A作AQ⊥CF,垂足为Q,交DE于点G,
则四边形AOEG是矩形,四边形OFQA是矩形,四边形GEFQ是矩形,DG∥CQ,
∵C(5,7),
∴OF=AQ=5,OE=AG=;
∵直线BP将△ABC面积分成2:3两部分,根据同高两个三角形的面积比等于对应底之比,得AD:DC=2:3或AD:DC=3:2即AD:AC=2:5或AD:AC=3:5,
∵DG∥CQ,
∴,
∴或,
∴=2或=3,
当=2时,y=x+2=4,
当=3时,y=x+2=5,
∴点D的坐标为(2,4)或(3,5),
当点D的坐标为(2,4)时,设直线BP的解析式为y=mx+n,
根据题意,得,
解得,
∴直线BP的解析式为y=-x+6,
当y=0时,-x+6=0,解得x=6,
∴点P的坐标为(6,0);
当点D的坐标为(3,5)时,设直线BP的解析式为y=hx+t,
根据题意,得,
解得,
∴直线BP的解析式为y=x+,
当y=0时,x+=0,解得x=13,
∴点P的坐标为(13,0);
综上所述,P的坐标为(6,0)或(13,0).
18.
解:如图,点即为所求.
19.
解:(1)连接CD、CB,如图1所示:
∵A(0,0)、C(2,2)、D(0,2)、B(2,0),
∴CD=CB=AB=AD=2,
∴四边形DABC是菱形
又
∴四边形ABCD是正方形,
∵E、F两点分别从点D和点B向下和向右以每秒一个单位速度移动,
∴DE=BF,
∵∠CDE=∠CBF=90°,
∴△CDE≌△CBF(SAS),
∴EC=FC,
S四边形CEAF=S四边形CEAB+S△CBF=S四边形CEAB+S△CDE=S正方形ABCD=CB CD=2×2=4,
故答案为:FC,4;
(2)∵△CDE≌△CBF,
∴EC=FC,∠DCE=∠BCF,
∵∠DCE+∠ECB=90°,
∴∠BCF+∠ECB=90°,即∠ECF=90°,
∴△ECF是等腰直角三角形,
当t=1时,DE=1,
在Rt△CDE中,由勾股定理得:CE===,
∴EF=CE=×=,
∵Q为EF中点,
∴CQ=EF==;
(3)∵BP∥CF,∠ECF=90°,
∴∠BPC=90°,
∴点P的轨迹在以BC为直径的圆弧上,
设BC的中点为G,连接AG,如图2所示:
当点P在AG上时,AP最短,
此时,PG=BG=1,
在Rt△ABG中,由勾股定理得AG===,
∴AP=AG﹣PG=﹣1,
∵BC∥DE,
∴∠AEP=∠GCP,
∵GC=GP,
∴∠GCP=∠GPC,
∵∠GPC=∠APE,
∴∠AEP=∠APE,
∴AP=AE=﹣1,
∴E(0,1﹣),
∴DE=2﹣(1﹣)=+1,
∴t=(+1)s,
故答案为:(+1)s;
设CE的解析式为:y=kx+b(k≠0),
将C(2,2)、E(0,1﹣)代入解析式得:,
解得:,
∴CE的解析式为:y=x+1﹣,
令y=0,x=3﹣,
∴K(3﹣,0),
∴BK=2﹣(3﹣)=﹣1,
∴=,
∴点K是线段AB的黄金分割点.
20.
(1)当和不平行时,结论①仍然成立.
如图,由已知,可得,和两两平行,
∴四边形是梯形.
∴为的中点,
∴是梯形的中位线.
∴.
∴.
∴.
(2)∵为的中点,
∴,.
∴
.
∴.
∴.
21.
(1)证明:如图1中,设的中点为.连接,,,.
四边形是平行四边形,
与互相平分且交于点,,
,
四边形是平行四边形,
与互相平分且交于点,
,,
,
,
四边形是平行四边形.
(2)①如图中,连接交于点,当时,四边形是菱形.
,,,
,
,
,
,
,
.
②在①的基础上,满足时,四边形是正方形,
易知,
,
,
.
③如图中,连接交于点,作于.
,
,
,,
,
,
当时,四边形是矩形,
.
故答案为:5,1,.
22.
解:(1)∵AB=4,点C和点D是线段AB的黄金分割点,
∴AC=BD=AB=×4=2﹣2,
∴DC=AC+BD﹣AB=2(2﹣2)﹣4=4﹣8;
故答案为:2﹣2,4﹣8;
(2)∵b为0,1的黄金数,且实数0<b<1,
∴(b﹣0)2=(1﹣b)(1﹣0),
b2+b﹣1=0,
b1=<0(舍),b2=>0,
∵a为0,1的白银数,且实数0<a<1,
∴(1﹣a)2=(a﹣0)(1﹣0),
a2﹣3a+1=0,
a1=>1(舍),a2=<1,
∴b﹣a=﹣=﹣2;
(3)∵m,n分别为k,t的黄金数和白银数,实数k<n<m<t,
∴
分两种情况:
i)当k≥0时,t=2k,
由①得:(m﹣k)2=(2k﹣m)(2k﹣k),
m2﹣km﹣k2=0,
m=k;
由②得:(2k﹣n)2=(n﹣k)(2k﹣k),
n2﹣5kn+5k2=0,
n=k,
∵k<n<m<t,
∴m=k,n=k
∴===;
ii)当k<0时,t=﹣2k,
由①得:(m﹣k)2=(﹣2k﹣m)(﹣2k﹣k),
m2﹣5km﹣5k2=0,
m=k;
由②得:(﹣2k﹣n)2=(n﹣k)(﹣2k﹣k),
n2+7kn+k2=0,
n=k>0,
∵k<n<m<t,
∴m>0,
∴m=k,n=k,
∴ ===;
综上,的值是或.
23.
解:(1)如图1中,连接BE,CF.
∵AB=AC=6,∠BAC=90°,AD⊥BC于点D,
∴BC==12,BD=CD=6,
∴AD=BD=DC=6,
∴∠DAB=∠DAC=45°,
∵△AEF是等腰直角三角形,
∴AE=AF
∵∠DAH=45°,
∴∠FAH=90°-∠DAH=45°,
∴EH=HF,
∵AE:DE=2:1,AE+DE=6,
∴AE=4,DE=2,
∴BE=,
∵AB=AC,AE=AF,∠BAC=∠EAF=90°,
∴∠BAC-∠CAE=∠EAF-∠CAE,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(SAS),
∴CF=BE=2,
∵EG=CG,EH=FH,
∴GH=CF=.
(2)结论:∠DGH=90°是定值.
理由:连接BE,CF,设CF交BE于点O,BE交AC于J.
∵AB=AC,AE=AF,∠BAC=∠EAF=90°,
∴∠BAC+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(SAS),
∴∠ABE=∠ACF,
∵∠AJB=∠CJO,
∴∠COJ=∠BAJ=90°,
∴CF⊥BE,
∵EH=HF,EG=GC,
∴GH∥CF,
∵CD=DB,CG=GE,
∴DG∥BE,
∴DG⊥GH,
∴∠DGH=90°.
(3)如图3中,取AC的中点J,连接BJ,JG.
由题意AJ=JC=3,AB=6,
∵∠BAJ=90°,
∴BJ==3,
∵AJ=JC,EG=CG,
∴JG=AE=2,
∵BG≤BJ+JG,
∴BG≤3+2,
∴BG的最大值为3+2.
24.
因为,
所以a=b,c=d,e=f,
所以.
25.
(1)如图1中,猜想:DM=EM.
理由:作EF∥AB交BC于F,
∵AB=AC,
∴∠ABC=∠C,
∵EF∥AD,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
,
∴△BDM≌△FEM,
∴DM=EM.
故答案为DM=EM.
(2)结论DM=EM.
理由:如图2中,作EF∥AB交CB的延长线于F,
∵AB=AC,
∴∠ABC=∠C,
∵EF∥AB,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
,
∴△BDM≌△FEM,
∴DM=EM.
(3)如图3中,作EF∥AB交CB的延长线于F,
∵EF∥AB,
∴∠F=∠ABC,
∵AB=AC,
∴∠ABC=∠C,
∴∠F=∠C,
∴EF=CE=4,
∵BD∥EF,
∴,
∴,
∴EM=2.8,
故答案为2.8.
26.
解:(1如图一,在矩形中,,,,
由折叠可得:,,
∴直角三角形中,,
∴,
设,则,
在中,,
解得,
即;
(2)如图二,当,且四边形为矩形时,点在的垂直平分线上,
即垂直平分,
∴,①
又∵,
∴,
∵,
∴,即
解得,②
∴由①②得:矩形的长宽比为,
在中,.
同课章节目录
