九年级数学上册试题 4.1比例线段同步练习-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.1比例线段同步练习-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 435.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 22:56:18 | ||
图片预览




文档简介
4.1比例线段
一、单选题
1.若,则等于( )
A. B. C. D.
2.下列命题中,错误的是( )
A.顺次连接矩形四边的中点所得到的四边形是菱形
B.反比例函数的图象是轴对称图形
C.线段的长度是,点是线段的黄金分割点且,则
D.对于任意的实数,方程有两个不相等的实数根
3.若,则等于( )
A. B. C. D.
4.已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( )
A.AB2=AC2+BC2 B.BC2=AC BA
C. D.
5.如果(其中,),那么下列式子中不正确的是( )
A. B. C. D.
6.若2x=5y,则的值是( )
A. B. C. D.
7.已知线段,点C是线段AB的黄金分割点(),则AC的长为( )
A. B. C. D.
8.某品牌汽车为了打造更加精美的外观,特将汽车倒车镜设计为整个车身黄金分割点的位置(如图),若车头与倒车镜的水平距离为1.58米,则该车车身总长约为( )米.
A.4.14 B.2.56 C.6.70 D.3.82
二、填空题
9.大自然巧夺天工,一片小小树叶,也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么的长度是______.
10.已知点P是线段AB的一个黄金分割点,且AP>BP,那么AP:AB的比值为______.
11.已知,则=_____.
12.已知点P在线段AB上,且AP∶PB=2∶3,则PB∶AB=____.
13.如图,在中,点是线段的黄金分割点(),若的面积是,则的面积是_______.
14.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”(黄金比为).如图,P为的黄金分割点(),如果的长度为,那么较长线段的长度为_______.
15.已知,则= .
16.若==(x,y,z均不为0),=1,则m的值为______ .
三、解答题
17.如图,在等腰和等腰中,底边的长,,它们的周长分别为和,那么这两个等腰三角形的腰与底边是否成比例线段,说明理由.
18.已知a:b:c=2:3:5,如果3a-b+c=24,求a,b,c的值.
19.已知,求的值.
20.如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
(1)若点D是BC的中点,
①若AP:PD=2:1,求AM:AB的值
②证明:;
(2)若点D是BC上任意一点,试证明:.
21.已知,求的值.
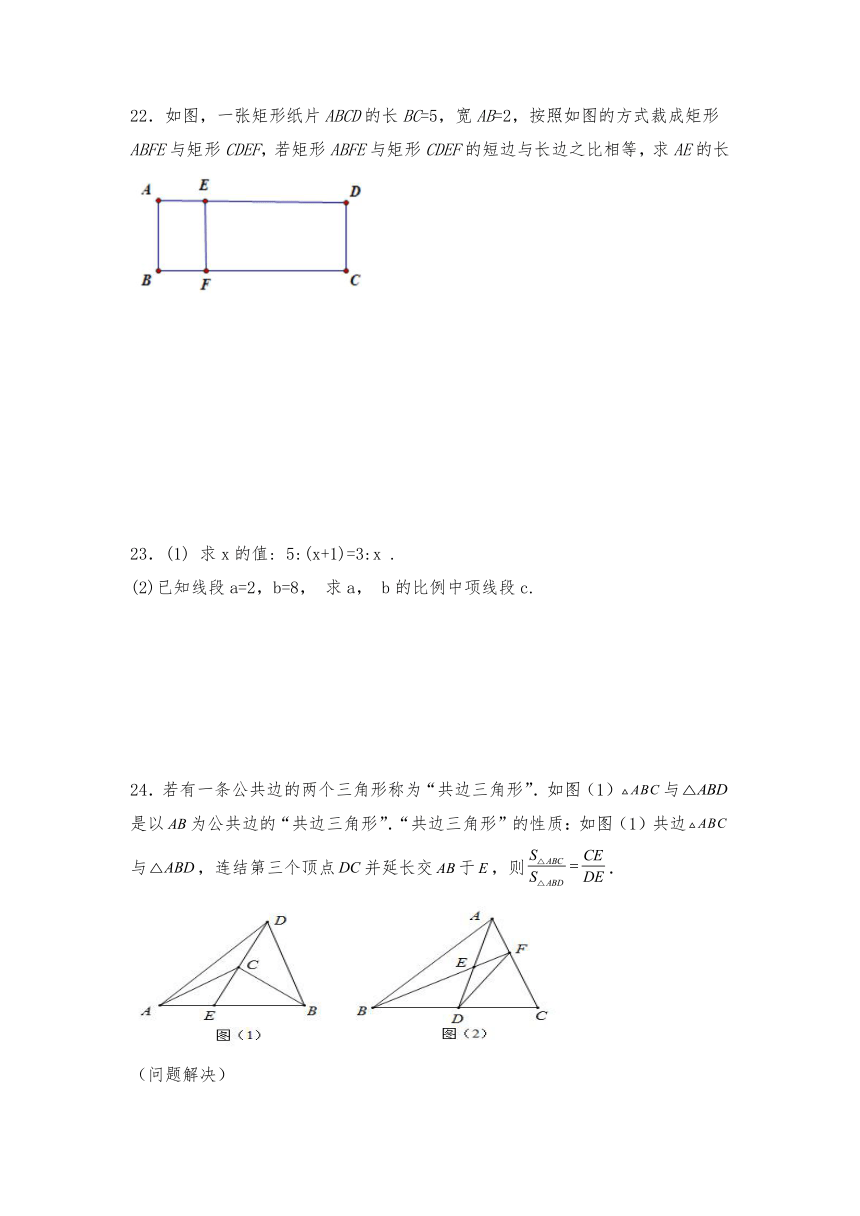
22.如图,一张矩形纸片ABCD的长BC=5,宽AB=2,按照如图的方式裁成矩形ABFE与矩形CDEF,若矩形ABFE与矩形CDEF的短边与长边之比相等,求AE的长
23.(1) 求x的值: 5:(x+1)=3:x .
(2)已知线段a=2,b=8, 求a, b的比例中项线段c.
24.若有一条公共边的两个三角形称为“共边三角形”.如图(1)与是以为公共边的“共边三角形”.“共边三角形”的性质:如图(1)共边与,连结第三个顶点并延长交于,则.
(问题解决)
如图(2),已知在中,为的中点,为的中点,的连线交于.
(1)找出以为公共边的所有“共边三角形”,若的面积为?,分别求出这些“共边三角形”的面积;
(2)求证:;
(3)若将“为的中点”条件,改为“”,则______.
25.已知:,求的值.
26.如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.
答案
一、单选题
B.C.C.C.D.B.C.A.
二、填空题
9..
10..
11..
12.3:5(或).
13..
14.6.18.
15..
16.4.
三、解答题
17.
这两个等腰三角形的腰与底边是成比例线段,理由如下:
∵在等腰和等腰中,底边的长,,
它们的周长分别为和,
∴,.
∵,,∴.
∴这两个等腰三角形的腰与底边是成比例线段.
18.
设a=2k,b=3k,c=5k(k≠0),则
6k-3k+5k=24,
解得k=3.
则a=2k=6,
b=3k=9,
c=5k=15.
19.
解:根据题意,设比值为,即,
则,,.
∴.
20.
(1)①过点D作DE∥PM交AB于E,
∵PM∥AC,∴DE∥AC,
.
∵点D为BC中点,
∴点E是AB中点,且,
∴;
②延长AD至点Q,使DQ=AD,连BQ、CQ,
∵DQ=AD,BD=DC,
四边形ABQC是平行四边形.
∴PM∥BQ,PN∥CQ,
∴,,
∴;(注:像第(1)题那样作辅助线也可以.)
(3)过点D作DE∥PM交AB于E,
∴,
又∵PM∥AC,∴DE∥AC,
∴,
∴,
同理可得:,
∴.
21.
解:,
,,.
,
.
情况一:如果,那么;
情况二:如果,那么,则.
22.
解:如图,因为AB=2,BC=5,EF=AB=2,DE=5-AE,
当时, 即
解得:
当时,
解得:
综上可得AE为1,4,或.
23.
解:(1)∵,
∴3(x+1)=5x,
∴3x+3=5x,
解得:x= 1.5;
(2)∵c 为线段 a,b 的比例中项,
∴c2= ab,即 c2=16,
∵c>0,
∴c=4.
24.
(1)解:由题意得:
以BF为公共边的“共边三角形”为:、、,
由“共边三角形”的性质:,,
∴,
∵的面积为,
∴,
∴;
(2)证明:由“共边三角形”的性质:
即:,
∴,
∴;
(3)解:由“共边三角形”的性质:,,
∴,
∵,
∴,
故答案为.
25.
解:由,可得2(4a﹣b)=3(5a+2b),
即8a﹣2b=15a+6b,
∴7a=﹣8b,
∴=﹣.
26.
解:M是AB的黄金分割点,理由如下:
∵正方形ABCD的边长为2,E为BC的中点,
∴BE=1
∴AE,
∵EF=BE=1,
∴AF=AE﹣EF1,
∴AM=AF1,
∴AM:AB=(1):2,
∴点M是线段AB的黄金分割点.
一、单选题
1.若,则等于( )
A. B. C. D.
2.下列命题中,错误的是( )
A.顺次连接矩形四边的中点所得到的四边形是菱形
B.反比例函数的图象是轴对称图形
C.线段的长度是,点是线段的黄金分割点且,则
D.对于任意的实数,方程有两个不相等的实数根
3.若,则等于( )
A. B. C. D.
4.已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( )
A.AB2=AC2+BC2 B.BC2=AC BA
C. D.
5.如果(其中,),那么下列式子中不正确的是( )
A. B. C. D.
6.若2x=5y,则的值是( )
A. B. C. D.
7.已知线段,点C是线段AB的黄金分割点(),则AC的长为( )
A. B. C. D.
8.某品牌汽车为了打造更加精美的外观,特将汽车倒车镜设计为整个车身黄金分割点的位置(如图),若车头与倒车镜的水平距离为1.58米,则该车车身总长约为( )米.
A.4.14 B.2.56 C.6.70 D.3.82
二、填空题
9.大自然巧夺天工,一片小小树叶,也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么的长度是______.
10.已知点P是线段AB的一个黄金分割点,且AP>BP,那么AP:AB的比值为______.
11.已知,则=_____.
12.已知点P在线段AB上,且AP∶PB=2∶3,则PB∶AB=____.
13.如图,在中,点是线段的黄金分割点(),若的面积是,则的面积是_______.
14.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”(黄金比为).如图,P为的黄金分割点(),如果的长度为,那么较长线段的长度为_______.
15.已知,则= .
16.若==(x,y,z均不为0),=1,则m的值为______ .
三、解答题
17.如图,在等腰和等腰中,底边的长,,它们的周长分别为和,那么这两个等腰三角形的腰与底边是否成比例线段,说明理由.
18.已知a:b:c=2:3:5,如果3a-b+c=24,求a,b,c的值.
19.已知,求的值.
20.如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
(1)若点D是BC的中点,
①若AP:PD=2:1,求AM:AB的值
②证明:;
(2)若点D是BC上任意一点,试证明:.
21.已知,求的值.
22.如图,一张矩形纸片ABCD的长BC=5,宽AB=2,按照如图的方式裁成矩形ABFE与矩形CDEF,若矩形ABFE与矩形CDEF的短边与长边之比相等,求AE的长
23.(1) 求x的值: 5:(x+1)=3:x .
(2)已知线段a=2,b=8, 求a, b的比例中项线段c.
24.若有一条公共边的两个三角形称为“共边三角形”.如图(1)与是以为公共边的“共边三角形”.“共边三角形”的性质:如图(1)共边与,连结第三个顶点并延长交于,则.
(问题解决)
如图(2),已知在中,为的中点,为的中点,的连线交于.
(1)找出以为公共边的所有“共边三角形”,若的面积为?,分别求出这些“共边三角形”的面积;
(2)求证:;
(3)若将“为的中点”条件,改为“”,则______.
25.已知:,求的值.
26.如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.
答案
一、单选题
B.C.C.C.D.B.C.A.
二、填空题
9..
10..
11..
12.3:5(或).
13..
14.6.18.
15..
16.4.
三、解答题
17.
这两个等腰三角形的腰与底边是成比例线段,理由如下:
∵在等腰和等腰中,底边的长,,
它们的周长分别为和,
∴,.
∵,,∴.
∴这两个等腰三角形的腰与底边是成比例线段.
18.
设a=2k,b=3k,c=5k(k≠0),则
6k-3k+5k=24,
解得k=3.
则a=2k=6,
b=3k=9,
c=5k=15.
19.
解:根据题意,设比值为,即,
则,,.
∴.
20.
(1)①过点D作DE∥PM交AB于E,
∵PM∥AC,∴DE∥AC,
.
∵点D为BC中点,
∴点E是AB中点,且,
∴;
②延长AD至点Q,使DQ=AD,连BQ、CQ,
∵DQ=AD,BD=DC,
四边形ABQC是平行四边形.
∴PM∥BQ,PN∥CQ,
∴,,
∴;(注:像第(1)题那样作辅助线也可以.)
(3)过点D作DE∥PM交AB于E,
∴,
又∵PM∥AC,∴DE∥AC,
∴,
∴,
同理可得:,
∴.
21.
解:,
,,.
,
.
情况一:如果,那么;
情况二:如果,那么,则.
22.
解:如图,因为AB=2,BC=5,EF=AB=2,DE=5-AE,
当时, 即
解得:
当时,
解得:
综上可得AE为1,4,或.
23.
解:(1)∵,
∴3(x+1)=5x,
∴3x+3=5x,
解得:x= 1.5;
(2)∵c 为线段 a,b 的比例中项,
∴c2= ab,即 c2=16,
∵c>0,
∴c=4.
24.
(1)解:由题意得:
以BF为公共边的“共边三角形”为:、、,
由“共边三角形”的性质:,,
∴,
∵的面积为,
∴,
∴;
(2)证明:由“共边三角形”的性质:
即:,
∴,
∴;
(3)解:由“共边三角形”的性质:,,
∴,
∵,
∴,
故答案为.
25.
解:由,可得2(4a﹣b)=3(5a+2b),
即8a﹣2b=15a+6b,
∴7a=﹣8b,
∴=﹣.
26.
解:M是AB的黄金分割点,理由如下:
∵正方形ABCD的边长为2,E为BC的中点,
∴BE=1
∴AE,
∵EF=BE=1,
∴AF=AE﹣EF1,
∴AM=AF1,
∴AM:AB=(1):2,
∴点M是线段AB的黄金分割点.
同课章节目录
