4.2 相似三角形

(共13张PPT)
观察 欣赏
观察 欣赏
生活中存在着许多图形相似变换的现象
三角形作为一个简单的几何图形，同样可以进行相似变换
4.2 相似三角形
执教：桂安林
C
A
B
B′
A′
C′
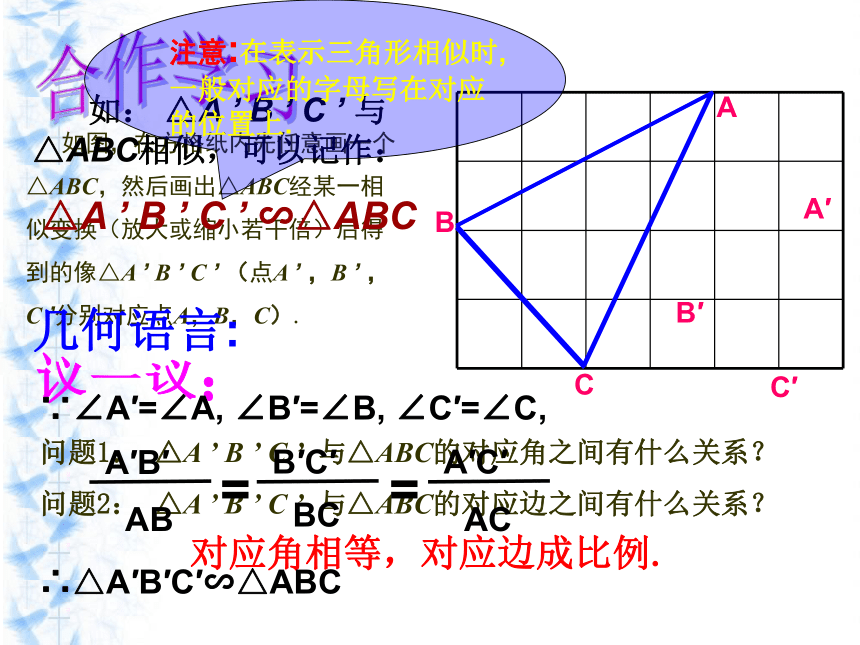
如图，在方格纸内先任意画一个△ABC，然后画出△ABC经某一相似变换（放大或缩小若干倍）后得到的像△A ’ B ’ C ’ （点A ’ ，B ’ ，C ’分别对应点A，B，C）.
问题1： △A ’ B ’ C ’ 与△ABC的对应角之间有什么关系？
问题2： △A ’ B ’ C ’ 与△ABC的对应边之间有什么关系？
对应角相等，对应边成比例.
如： △A ’ B ’ C ’ 与△ABC相似，可以记作：
△A ’ B ’ C ’ ∽△ABC
注意:在表示三角形相似时,一般对应的字母写在对应的位置上.
几何语言:
∵∠A′=∠A, ∠B′=∠B, ∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
∴△A′B′C′∽△ABC
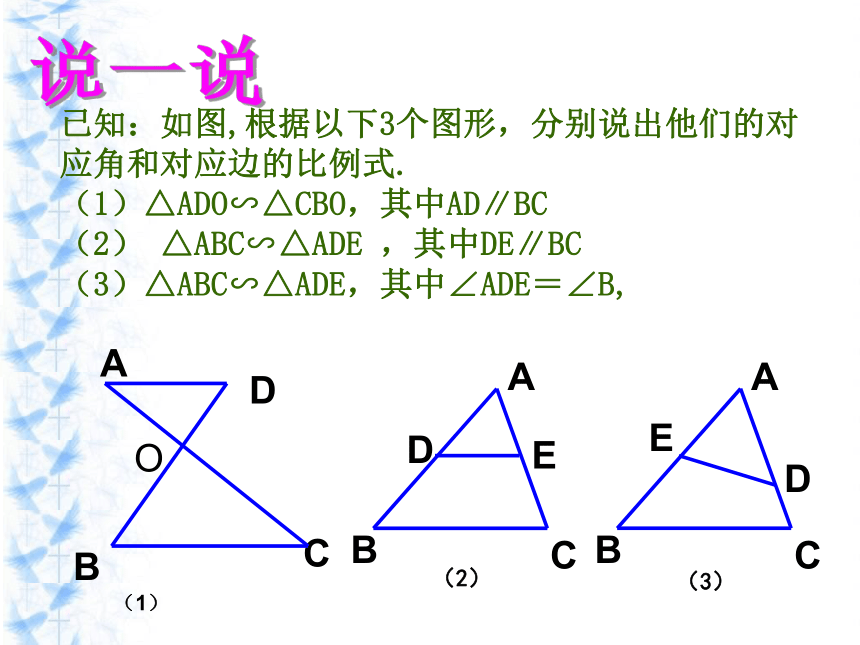
已知：如图,根据以下3个图形，分别说出他们的对应角和对应边的比例式.
（1）△ADO∽△CBO，其中AD∥BC
（2） △ABC∽△ADE ，其中DE∥BC
（3）△ABC∽△ADE，其中∠ADE＝∠B,
E
D
C
B
A
（2）
E
D
C
B
A
（3）
D
A
B
C
O
（1）
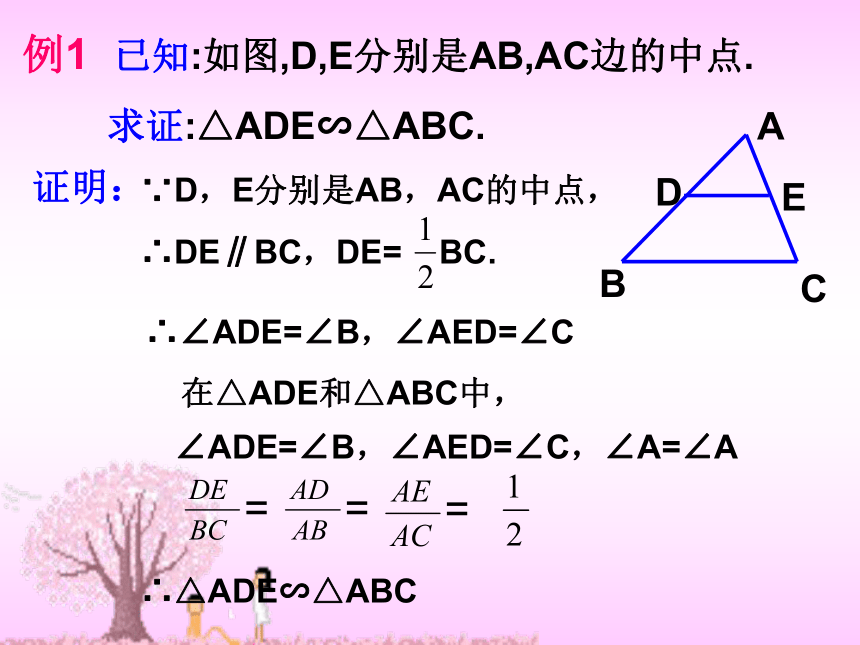
例1 已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
E
D
C
B
A
证明：
∵D，E分别是AB，AC的中点，
∴∠ADE=∠B，∠AED=∠C
在△ADE和△ABC中，
∠ADE=∠B，∠AED=∠C，∠A=∠A
=
=
=
∴DE∥BC，DE= BC.
∴△ADE∽△ABC
判定下列说法是否正确，正确的打“√”，错误的打“×”，并说明理由.
1.两个等腰三角形一定相似.………………（ ）
2.两个直角三角形一定相似.………………（ ）
3.两个等边三角形一定相似.………………（ ）
4.两个等腰直角三角形一定相似…………（ ）
5. 两个全等三角形一定相似…………（ ）
√
√
×
×
√
根据相似三角形的定义，你能归纳出相似三角形的性质吗？
B
A
C
B′
A′
C′
相似三角形的对应角相等，对应边成比例.
如图，∵ △A′B′C′∽△ABC
∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数) (similitude ratio).
如图， ，所以△A′B′C′与△ABC的相似比为 ，
A′B′
AB
=
△ABC与△A′B′C′的相似比为 .
那么全等三角形的 相似比为————。
2
注意:两个三角形的前后顺序.
1
例2 已知：如图，D，E分别是△ABC的AB，AC边上的点， △ABC∽△ADE.已知AD﹕DB=1﹕2，BC=9cm，求DE的长.
E
D
C
B
A
温馨提示： AD:DB的比是△ADE与△ABC的相似比吗
1.课本P.105_课堂练习1.
2.如图，有一块呈三角形形状的草坪，其最大边长是20m.在这个草坪的示意图上，最大边长为5cm，其余他两边的长度都分别3 cm和4cm.求该草坪其他两边的实际长度.
找出各题中的其他对应角和对应边的比例式.
(4) △ADE∽△ABC, ∠D =∠B
(5) △ADE∽△ABC, ∠D=∠B, ∠BAD=∠CAE
(6) △CBD∽△ABC，CD⊥AB, ∠ACB=90°
A
E
B
C
D
（4）
A
B
D
E
（5）
C
C
A
D
B
（6）
同学们，通过这一节课的学习，你有哪些收获与体会呢？能让大家一起分享你的成功与喜悦吗？
1.对应角相等，对应边成比例的三角形，叫做相似三角形（similar triangle）.
3.相似三角形的对应边的比，叫做两个相似三角形的相似比（或相似系数）.
2.相似三角形的对应角相等，对应边成比例.