2.2 有理数的减法
图片预览






文档简介
课件23张PPT。2.2.1 有理数的减法问题一:呼和浩特在一天的最高气温是19 ℃ ,最低气温是7 ℃ ,问这一天内呼和浩特的温差是多少?怎么计算?问题二:厦门的最高气温是9 ℃ ,哈尔滨的最高气温是-7 ℃ ,问这天厦门的最高气温比哈尔滨的最高气温高多少摄氏度?可以怎样计算?问题三:哈尔滨的最高温度是-7℃,最低温度为-12℃,这天哈尔滨的温差是多少?你是怎么算的?问一问什么数加上
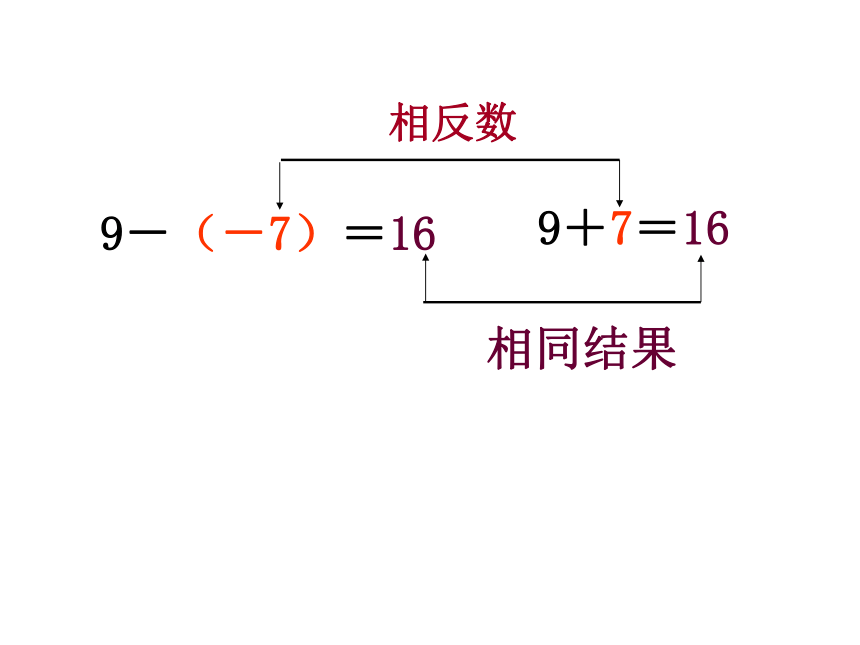
-7等于9呢? 9-(-7)=?想一想:16+(-7)=9问题一:19-7=129-(-7)=16 相反数相同结果9+7=16计算下列各题:观察、对比每横行的两个算式,你能得出什么结论?减去一个数,等于加上这个数的相反数
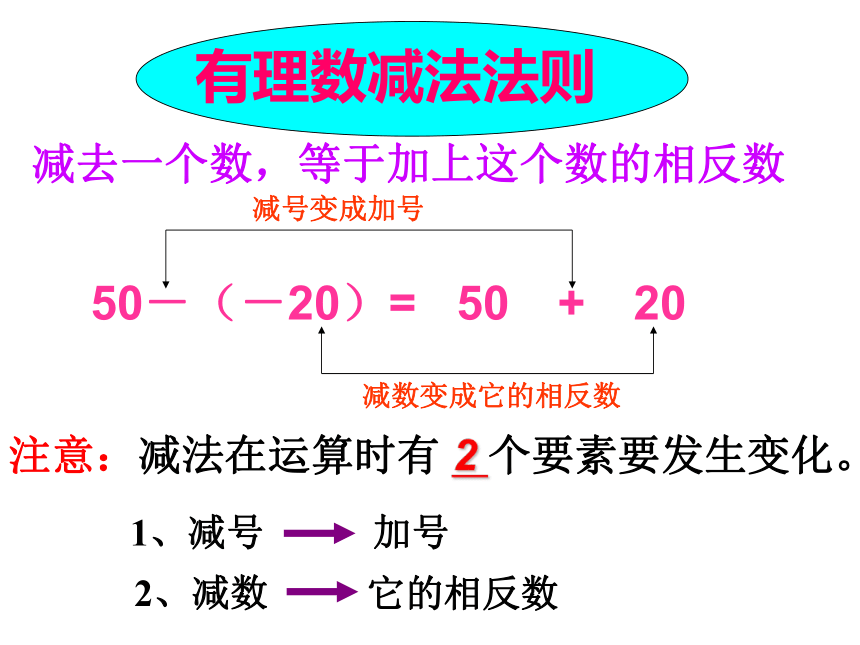
有理数减法法则注意:减法在运算时有 2 个要素要发生变化。1、减号加号它的相反数2、减数 50-(-20)= 50 + 20减号变成加号减数变成它的相反数 有理数减法法则
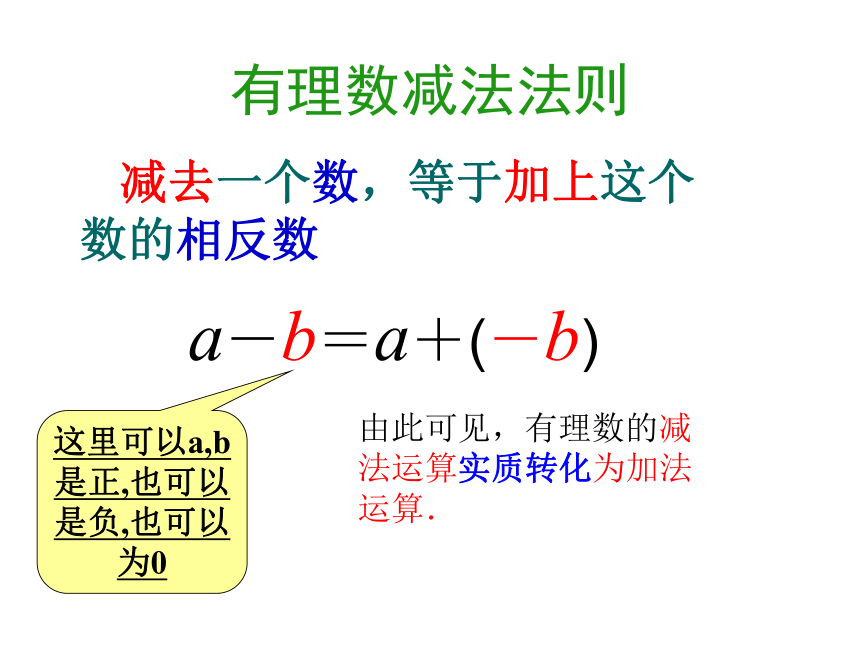
减去一个数,等于加上这个数的相反数a-b=a+(-b)这里可以a,b
是正,也可以
是负,也可以
为0由此可见,有理数的减法运算实质转化为加法运算. 例1、计算下列各题:
(1)5-(-5) (2)0-7-5
(3)(-1.3)-(-2.1)(4)解(1) 5-(-5)=5 + 5= 10
(2)0-7-5=0+(-7)+(-5)=-7+(-5)=-12
(3)(-1.3)-(-2.1)=(-1.3)+2.1=2.1-1.3=0.8
(4) 有理数的减法法则
减去一个数,等于加上这个数的相反数. 解法指导:
先把减法变加法,
再依加法法则计算.做题时要想着法则随堂练习:1、口算:
(1)3-5=___; (2) -5 -3=___;
(3)(-3)-5=_____;(4)(-3)-(-5)=____;
(5)-6-(-6)=___;(6)-7-0=___;
(6)0-7=___;
(7)0-(-3)=0+( )=____
(9) 13-(-13)=13+( )= _____-2-8-820-7-73313262.填空
⑴-9+( )=16; ⑵42+( )=-25;
⑶( )-(-18)=35; ⑷( )-87=-2125-6717663.课本31页课内练习2
例2:我国吐鲁番盆地最低点的海拔高度是-155米,死海的湖面低于海平面392米。哪里的海拔高度更低?低多少米?解:死海的湖面低于海平面392米,即海拔高度是-392米。
-392-(-155)=-392+155=-237(米)。
答:两者相比,死海的湖面更低,比吐鲁番盆地最低点低237米。 在有理数范围内,
不存在“不够减”的减法
世界上最高的山峰是珠穆朗玛峰,其海拔高度大约是8 848米,吐鲁番盆地的海拔高度大约是-155米.两处高度相差多少米?解:8 848-(-155)=8 848+155=9 003(米).因此,两处高度相差9 003米.练一练1:练一练2:某潜艇从海平面以下27米处上升到海平面以下18米处,此潜艇上升了多少米?例3 全班学生分为五组进行游戏,每组的基本分为100
分,答对一题加50分,答错一题扣50分.游戏结束时,
各组的分数如下:(1)第一名超出第二名多少分?
(2)第一名超出第五名多少分?解:由上表可以看出,第一名得了350分,第二名得了
150分,第五名得了-400分.(1)350-150=200(分);(2)350-(-400)=750(分).因此,第一名超出第二名200分,第一名超出第五名750分.拓展:已知两数的和是最大的负整数,其中一个加数是最小的正整数,求另一个加数.解:因为最大的负整数是-1,最大的正整数是1,由题意得:
-1-1=-2
答:另一个加数是-2.做课本31页课内练习3
请你仔细想一想 一个数与它的相反数的差是什么数?你能举例加以说明吗?答:一个数与它的相反数的差是这个数的2倍,如4与它的相反数(-4)的差:4-(-4)=8,8是4的2倍;再如-5与它的相反数5的差:-5-5=-10,-10是-5的2倍.练一练已知一个数与3的和是-10,求这个数.1、通过上面的练习,你能总结出有理数减法与小学里学过的减法的不同点吗? (1)被减数可以小于减数.如: 1-5 ;
(2)差可以大于被减数,如:(+3)-(-2);
(3)有理数相减,差仍为有理数;
(4)大数减小数,差为正数;小数减大数,差为负数; 2、根据有理数减法的法则,一切加法和减法的运算,都可以统一成加法运算. 小结: 有理数的减法法则
减去一个数,等于加上这个数的相反数.a-b=a+(-b)拓展提高:计算:
(1) (-72) -(-37) -(-22) -17
(2) (-16) -(-12) -24- (-18)
(3) 〔8+(-5) 〕- 13
(4) 3/2 -〔(-1.5)+ 0.5〕作业:1、作业本 “有理数的减法(一)”
2、课本第31、32页作业题1-6再见!谢谢大家
-7等于9呢? 9-(-7)=?想一想:16+(-7)=9问题一:19-7=129-(-7)=16 相反数相同结果9+7=16计算下列各题:观察、对比每横行的两个算式,你能得出什么结论?减去一个数,等于加上这个数的相反数
有理数减法法则注意:减法在运算时有 2 个要素要发生变化。1、减号加号它的相反数2、减数 50-(-20)= 50 + 20减号变成加号减数变成它的相反数 有理数减法法则
减去一个数,等于加上这个数的相反数a-b=a+(-b)这里可以a,b
是正,也可以
是负,也可以
为0由此可见,有理数的减法运算实质转化为加法运算. 例1、计算下列各题:
(1)5-(-5) (2)0-7-5
(3)(-1.3)-(-2.1)(4)解(1) 5-(-5)=5 + 5= 10
(2)0-7-5=0+(-7)+(-5)=-7+(-5)=-12
(3)(-1.3)-(-2.1)=(-1.3)+2.1=2.1-1.3=0.8
(4) 有理数的减法法则
减去一个数,等于加上这个数的相反数. 解法指导:
先把减法变加法,
再依加法法则计算.做题时要想着法则随堂练习:1、口算:
(1)3-5=___; (2) -5 -3=___;
(3)(-3)-5=_____;(4)(-3)-(-5)=____;
(5)-6-(-6)=___;(6)-7-0=___;
(6)0-7=___;
(7)0-(-3)=0+( )=____
(9) 13-(-13)=13+( )= _____-2-8-820-7-73313262.填空
⑴-9+( )=16; ⑵42+( )=-25;
⑶( )-(-18)=35; ⑷( )-87=-2125-6717663.课本31页课内练习2
例2:我国吐鲁番盆地最低点的海拔高度是-155米,死海的湖面低于海平面392米。哪里的海拔高度更低?低多少米?解:死海的湖面低于海平面392米,即海拔高度是-392米。
-392-(-155)=-392+155=-237(米)。
答:两者相比,死海的湖面更低,比吐鲁番盆地最低点低237米。 在有理数范围内,
不存在“不够减”的减法
世界上最高的山峰是珠穆朗玛峰,其海拔高度大约是8 848米,吐鲁番盆地的海拔高度大约是-155米.两处高度相差多少米?解:8 848-(-155)=8 848+155=9 003(米).因此,两处高度相差9 003米.练一练1:练一练2:某潜艇从海平面以下27米处上升到海平面以下18米处,此潜艇上升了多少米?例3 全班学生分为五组进行游戏,每组的基本分为100
分,答对一题加50分,答错一题扣50分.游戏结束时,
各组的分数如下:(1)第一名超出第二名多少分?
(2)第一名超出第五名多少分?解:由上表可以看出,第一名得了350分,第二名得了
150分,第五名得了-400分.(1)350-150=200(分);(2)350-(-400)=750(分).因此,第一名超出第二名200分,第一名超出第五名750分.拓展:已知两数的和是最大的负整数,其中一个加数是最小的正整数,求另一个加数.解:因为最大的负整数是-1,最大的正整数是1,由题意得:
-1-1=-2
答:另一个加数是-2.做课本31页课内练习3
请你仔细想一想 一个数与它的相反数的差是什么数?你能举例加以说明吗?答:一个数与它的相反数的差是这个数的2倍,如4与它的相反数(-4)的差:4-(-4)=8,8是4的2倍;再如-5与它的相反数5的差:-5-5=-10,-10是-5的2倍.练一练已知一个数与3的和是-10,求这个数.1、通过上面的练习,你能总结出有理数减法与小学里学过的减法的不同点吗? (1)被减数可以小于减数.如: 1-5 ;
(2)差可以大于被减数,如:(+3)-(-2);
(3)有理数相减,差仍为有理数;
(4)大数减小数,差为正数;小数减大数,差为负数; 2、根据有理数减法的法则,一切加法和减法的运算,都可以统一成加法运算. 小结: 有理数的减法法则
减去一个数,等于加上这个数的相反数.a-b=a+(-b)拓展提高:计算:
(1) (-72) -(-37) -(-22) -17
(2) (-16) -(-12) -24- (-18)
(3) 〔8+(-5) 〕- 13
(4) 3/2 -〔(-1.5)+ 0.5〕作业:1、作业本 “有理数的减法(一)”
2、课本第31、32页作业题1-6再见!谢谢大家
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
