4.2 代数式

课件20张PPT。4.2 代数式复习与回顾利用字母表示数来表示下列数学规律：1.任何一个负数的绝对值大于他本身；2.任何一个不为0的数与它的倒数的积等于1；3.两个互为相反数的数的和为零；4.一个数的立方根的立方就是这个数本身；(2)大米的单价为a元/千克,食用油的单价为b元/千克.买10千克大米,2千克食用油共需________ 元;(3)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值.若上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数是_____________。(4)一五彩花圃的形状如下图,花圃的面积为______。用字母表示数量关系:(1)一隧道长L米，一列火车长180米，如果该列火车穿过
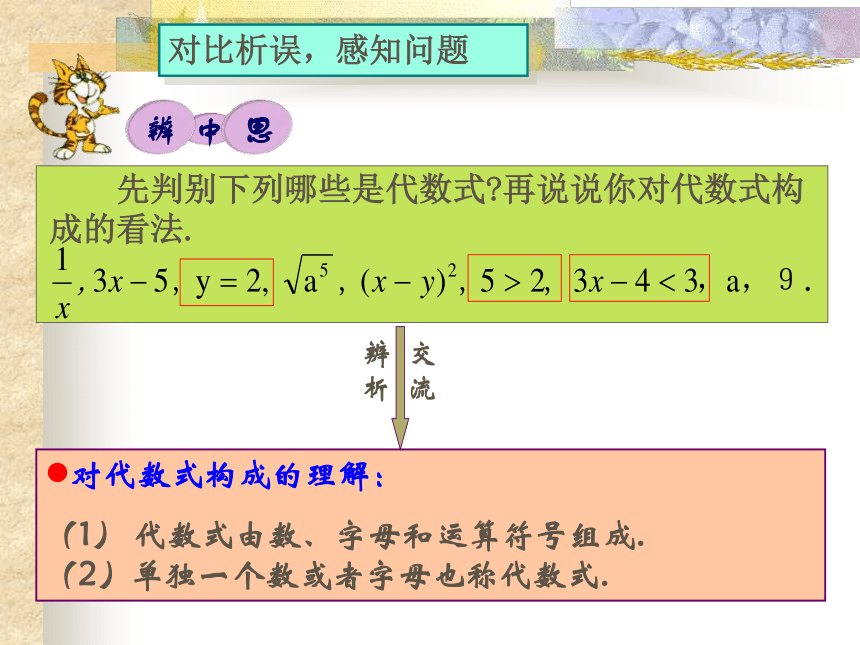
隧道所花的时间为t小时，则火车的速度是 米/时。(2) b÷a通常写作 ;像 这样含有字母的数学表达式称为代数式。一个代数式由数、字母、运算符号组成. (3) 数字通常写在字母前面;(1) a×b通常写作a·b或ab；如：a×3通常写作3a(4) 带分数一般写成假分数.代数式的规范写法：｛规定: 单独一个数或一个字母也称代数式。对比析误，感知问题 先判别下列哪些是代数式?再说说你对代数式构成的看法.对代数式构成的理解：
（1） 代数式由数、字母和运算符号组成. （2）单独一个数或者字母也称代数式.辨 交析 流 判断下列代数式书写是否规范，将不规范的改正。
?????????????????????
(1) (2)(3) (4)(5)用代数式表示:
x的 倍与3的差；
2a的立方根；变式1：a与b的平方的和；
变式2：a、b两数的平方和．大家一起来 式列 a与b的和的平方.变式: m的2倍除n所得的商 m的2倍除以n所得的商； m的2倍除以n所得的商；归纳：代数式可以简明地,具有普遍意义地表示实际问题中的量，给数量关系的研究带来方便!做一做１.用代数式表示:
(1)a与b的1/2的和;
(2)a与b的平方的差;
(3)m与n的差的平方;
(4)c与d的和除s所得的商;
(5)x与1的差的平方根;２.已知甲数比乙数的2倍少1，设乙数为x，用关于x的代数式表示甲数。例例3、用文字叙述下列代数式的意义：
（1）a－b2；
（2）|a|－|b|；
（3）(x2－y2)＋(x－y)2。（1）a与b的平方的差；
（2）a的绝对值与b的绝对值的差；
（3）x与y的平方差与x与y的差的平方的和。用文字叙述下列代数式的意义： a与b的平方的差。 a与b的差的平方。8与a的立方的积。a与b的立方和。解:由题意得,A,B两城之间的路程为80t千米.如果该车的行驶速度增加了v千米/时,那么汽车的行驶速度为(80+v)千米/时,此时从A城到B城需例2:一辆汽车以此80千米/时速度行驶,从A城到B城需t时.如果该车的行驶速度增加了v千米/时,那么从A城到B城需多少时间?1、一个两位数的个位数字是a，十位数字是b，请用代数式表示这个两位数。
2、如何用代数式表示一个三位数？想 一 想练一练(2) a+m-1a+1aa+1 +1a +1 +1+ …+1m-1…第1排第2排第3排第m排…{合作交流，解决问题主题2：右图是赵爽在《周髀算经》中作的“弦图” ，它由四个完全一样的直角三角形拼成．请你用代数式表示大正方形的面积．
主题1：小明在玩火柴棒游戏时得到如下结果，请你动手摆一摆，并探索：摆出6个三角形至少需多少火柴棒？10个呢？ n个呢?若摆成正方形呢？探索(1)开动脑筋齐3+2(n-1), 3n-(n-1) , n+(n+1) , 2n+1, … 1、已知含盐的质量分数为30﹪的盐水x克，则代数式(1－30﹪)x表示的是什么？
2、3支球队进行单循环比赛（参加比赛的每一支球队都与其他所以球队各赛一场），总比赛场数是多少？4支球队呢？5支球队呢？m 支球队呢？探究补充： 现有甲种糖果a千克，售价每千克m元；乙种糖果b千克，售价每千克n元，若将这两种糖果混在一起出售，则售价应为每千克多少元？ 一隧道长b米，一列火车长180米。如果该火车穿过隧道所花的时间为t分，则列车的速度怎么表示？课堂小结：用代数式表示数量关系时,要正确理解语句的含义,搞清楚数与字母的运算关系,及运算顺序!说一说：你今天学到什么？？(1)作业本:4.2代数式(2)同步练习:4.2代数式再见！