一元一次方程的复习

课件38张PPT。一元一次方程复习走进数学——
你会发觉生活中处处都有她的身影；
你会发现许多令人惊喜的东西；
你还会感到自己变得越来越聪明、越来越有本领。
许多以前不会解决的问题、不会做的事情，现在
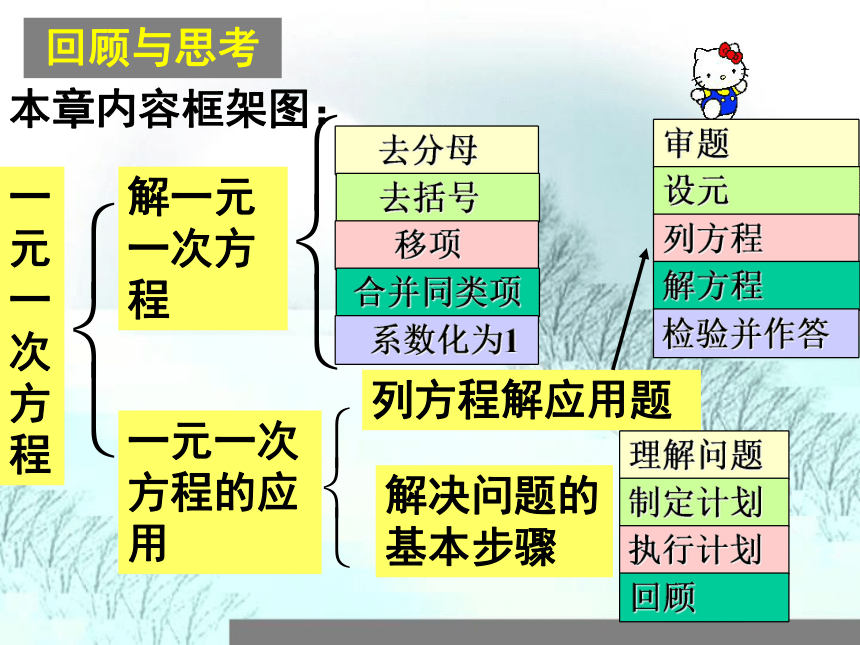
都能干得很好了！回顾与思考本章内容框架图：一元一次方程解一元一次方程一元一次方程的应用 去分母 去括号 移项 合并同类项 系数化为1列方程解应用题审题设元列方程解方程检验并作答解决问题的基本步骤理解问题制定计划执行计划回顾解一元一次方程的一般步骤变形名称注意事项去分母去括号移项合并同类项(ax=b)方程两边同除以未知数的系数a防止漏乘（尤其整数项），注意添括号；注意变号，防止漏乘；移项要变号，防止漏项；计算要仔细，不要出差错；计算要仔细，不要出差错；列方程解应用题的一般步骤 1、审题：分析题意，找出题中关键词及数量关系。
2、设元：选择一个适当的未知数用字母表示。 3、列方程：根据等量关系列出方程； 4、解方程，求出未知数的值；
5、检验并作答：检验求得的值是否正确、合理；写出答案。一填空题
1、一个数x的2倍减去7的差, 得36 ,列方程为____________；
2、方程5 x – 6 = 0的解是x =________；
3、日历中同一竖列相邻三个数的和为63，则这三个数分别为_____________；
4、 方程去分母得： .练 习 题2x-7=361.214、21、28.5x-10 = 2x5、一根长18米的铁丝围成一个长是宽的2倍的 长方形,这个长方形的面积为 ；6、一件衬衫进货价60元,提高50%后标价,则标 价为 _____, 八折优惠价为______,利润 为______；18平方米90元72元12元7、鸡兔同笼共9只，腿26条, 则鸡_____只， 兔_____只；8、小明每秒钟跑4米，则他15秒钟跑___米, 2分钟跑______米,1小时跑_____公里.546048014.4三、选择题1、方程 3x －5 = 7＋2 x 移项后得-------------（ ） A. 3x－2 x = 7－5 ，B. 3x＋2 x = 7－5 ， C. 3x＋2 x = 7＋5 ，D. 3x－2 x = 7＋5 ；2、方程 x －a = 7 的解是x =2，则a = --------（ ） A. 1 ， B. －1 ， C. 5 ， D. －5 ；3、方程 去分母后可得-----（ ） A. 3 x－3 =1＋2 x ，B. 3 x－9 =1＋2 x ， C. 3 x－3 =2＋2 x ，D. 3 x－12=2＋4 x ；DDB4、日历中同一竖列相邻三个数的和可以是----（ ） A 78 ， B 26 ， C 21 ， D 45 5、下列不是一元一次方程的是--------------------（ ） A 4 x－1 = 2 x ， B 3x－2 x = 7 ， C x－2 = 0 ， D x = y ；6、某商品提价100%后要恢复原价，则应降价-（ ） A 30% ， B 50% ， C 75% ， D 100% ； DDB
7、小明每秒钟跑6米，小彬每秒钟跑5米，小彬站在小
明前10米处，两人同时起跑，小明多少秒钟追上
小彬 --------------------------------------------（ ） A 5秒， B 6秒， C 8秒， D 10秒； 8、小山上大学向某商人贷款1万元，月利率为6‰ ，
1年后需还给商人多少钱？-----------------（ ） A 17200元， B 16000元，
C 10720元， D 10600元DC9、方程 是一元一次方程，则a和m分别为-------（ ）
A 2和4 ， B －2 和 4 ，
C 2 和 －4 ， D －2 和－4 。B三 解下列方程1.解：合并同类项，得：移项，得：方程两边同除以
-1，得：解：去括号，得：移项，得：合并同类项，得：方程两边同
除以-1，得： 解、去分母，得：去括号，得： 移项，得：合并同类项，得：方程两边同
除以-1，得：3.去分母，得：去括号，得： 移项，得：合并同类项，得：方程两边同除以13，得：解：原方程可化为：4.用一元一次方程分析和解决实际问题的基本过程如下:实际问题数学问题已知量,未知量,等量关系一元一次方程方程的解解的合理性实际问题答案抽象分析列出求出验证合理1、元旦某公园的成人的门票每张8元，儿童门票半价（即每张4元），全天共售出门票3000张，收入15600元。问这天售出儿童门票多少张？解：设售出儿童门票x张根据题意，得：解方程，得： x = 2100答：共售出儿童票2100张 2、某公司存入银行甲、乙两种不同性质的存款共20万元。甲种存款的年利率为1.4%，乙种存款的年利率为3.7%，该公司一年共得利息6250元，求甲、乙两种存款各多少元？解：设甲种存款为x万元。则乙种存款为（20 - x)万元根据题意得：解方程得： x = 5
所以 20 – x = 15答：甲种存款为5万元，乙种存款为15万元 3、某部队开展支农活动，甲队27人，乙队19人，现另调26人去支援，使甲队是乙队的2倍，问应调往甲队、乙队各多少人？解：设调往甲队x人，则调往乙队（26-x)人根据题意，得方程：解方程得：x = 21答：调往甲队21人。调往乙队5人。 4、日历中2×2方块的四个数的和是72，求
这四个数。解：设四个数中最小的数为x,根据题意，得方程：解方程，得：x = 14答：这四个数分别为14，15，21，22。某服饰有限公司准备加工一披演出服。在加工60套后，采用了新技术，使每天的工作效率从原来每天加工20套变为原来的2倍，结果共用9天完成任务。求该公司加工的这披演出服共多少套？解:设该公司加工的这披演出服共X套60 ＋2 ×20 ×（9 －60÷20）= X解得， X=300答：设该公司加工的这披演出服共300套。解:设该公司加工的这披演出服共X套解得， X=300答：设该公司加工的这披演出服共300套。等量关系１：原技术工作量＋新技术工作量＝总工作量等量关系２：原技术时间＋新技术时间＝总时间某服饰有限公司准备加工一披演出服。在加工60套后，采用了新技术，使每天的工作效率从原来每天加工20套变为原来的2倍，结果共用9天完成任务。求该公司加工的这披演出服共多少套？解:设该公司加工的这披演出服共X套（9 －60÷20） ×２ × ２０ = X－６０解得， X=300答：设该公司加工的这披演出服共300套。等量关系３：新技术时间×新技术效率＝新技术工作量解:设该公司加工的这披演出服共X套解得， X=300答：设该公司加工的这披演出服共300套。等量关系４：新技术效率＝２原技术效率 在一条笔直的公路上,小聪和小明骑自行车同时从相距500米的A.B两地出发,小聪每分钟行200米,小明每分行250米,问多少时间后,两人相距2000米?
你能与你的小伙伴一起模拟这个过程吗？学以致用哦！ 在一条笔直的公路上,小聪和小明骑自行车同时从相距500米的A.B两地出发,小聪每分钟行200米,小明每分行250米,问多少时间后,两人相距2000米?当小明在前,同向而行时,需x分钟相距2000米小明小聪AB?小明小聪250x+500=2000+200x 在一条笔直的公路上,小聪和小明骑自行车同时从相距500米的A.B两地出发,小聪每分钟行200米,小明每分行250米,问多少时间后,两人相距2000米?当小聪在前,同向而行时,需x分钟相距2000米小明小聪AB小明小聪250x=2000+500+200x? 在一条笔直的公路上,小聪和小明骑自行车同时从相距500米的A.B两地出发,小聪每分钟行200米,小明每分行250米,问多少时间后,两人相距2000米?当两人相背向行时,需x分钟相距2000米?小明小聪AB小明小聪250x+200x+500=2000 在一条笔直的公路上,小聪和小明骑自行车同时从相距500米的A.B两地出发,小聪每分钟行200米,小明每分行250米,问多少时间后,两人相距2000米?当两人相向而行时,需x分钟相距2000米?小明小聪AB小明小聪250x+200x=2000+500在解较复杂的行程问题时，可利用数形结合的思想，借助线段图来分析问题中的数量关系 小明在公路上行走，速度每分钟33米，一辆长为30米的汽车从他的背后驶来，经过他身旁驶过的时间是3秒，则汽车的速度为每小时多少千米 ？ 思考题 一队学生去校外进行军车野营训练，他们以5千米／时的速度前进，走了18分钟的时候，学校要将一个紧急通知传给队长，通讯员从学校出发，骑自行车以14千米／时的速度按原路追上去，通讯员用多少时间可以追上学生队伍？
情境5:爸爸刚回到家，就迫不急待地说：小哲 ，我有一件礼物要送给你，不过你要先回答好我的问题。他说：我们公司为了提高生产效益，准备派一些员工出差学习。有10人去广州，有3人去上海，需从去广州的人中调多少人到上海，使得去广州的是去上海的人数的2倍多1人。 (只列方程不解答)
分析： 数量关系如下所示： 广州 上海解：设需从去广州的人中调x人到上海，根据题意，得
10- x=2（ 3+ x ）+1
10- x 等量关系：调动后去广州的人数=调动后去上海人数的2倍多1人
加油噢3+ x 情境6：小哲轻松破解难题，他接下礼物，原来爸爸在浙北大厦为他买了他盼望已久的高级五彩橡皮泥。小哲灵机一动说：“爸爸，我也有一个小问题，如果你能答对，我也送你一件礼物。若用一块橡皮泥先做成一个圆柱体，其半径为1cm,高为9 cm，再把它改成立方体，你知道立方体的表面积吗？（圆柱体体积=底面积×高，π取3 ）
分析: 等量关系:圆柱体的体积=立方体的体积
情境7：小哲的妈妈所在的服装厂加工车间有工人54人，每人每天可加工上衣8件或裤子10条，应怎样合理分配人数，才能使每天生产的上衣和裤子配套？ 用如图1的长方形和正方形纸板作侧面和底面，做成如图2竖式和横式的两种无盖纸盒，现在仓库里有1000张正方形纸板和2000张长方形纸板，问两种纸盒各做多少只，恰好使库存的纸板用完？图 1图 2等量关系是什么？功夫用在刀刃上23142x3x1000－2x4(1000－2x)200010003x+ 4(1000－2x)= 200023142x3x1000－2x2000－3x200010002000－3x= 4(1000－2x)2314x4x－x1.5(1000－x)200010001.5(1000－x)+ 4x = 2000 用如图1的长方形和正方形纸板作侧面和底面，做成如图2竖式和横式的两种无盖纸盒，现在仓库里有1000张正方形纸板和2000张长方形纸板，问两种纸盒各做多少只，能否恰好使库存的纸板用完？5001001再 变3x+ 4(1000－2x)= 20001.5(1000－x)+ 4x = 2000解法1：设做x个横式纸盒解法2：设做x个竖式纸盒3x+ 4(500－2x)= 10011.5(500－x)+ 4x = 1001