浙教版九年级数学上册试题 1.2二次函数的图象同步测试(含答案)
文档属性
| 名称 | 浙教版九年级数学上册试题 1.2二次函数的图象同步测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 696.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:53:19 | ||
图片预览

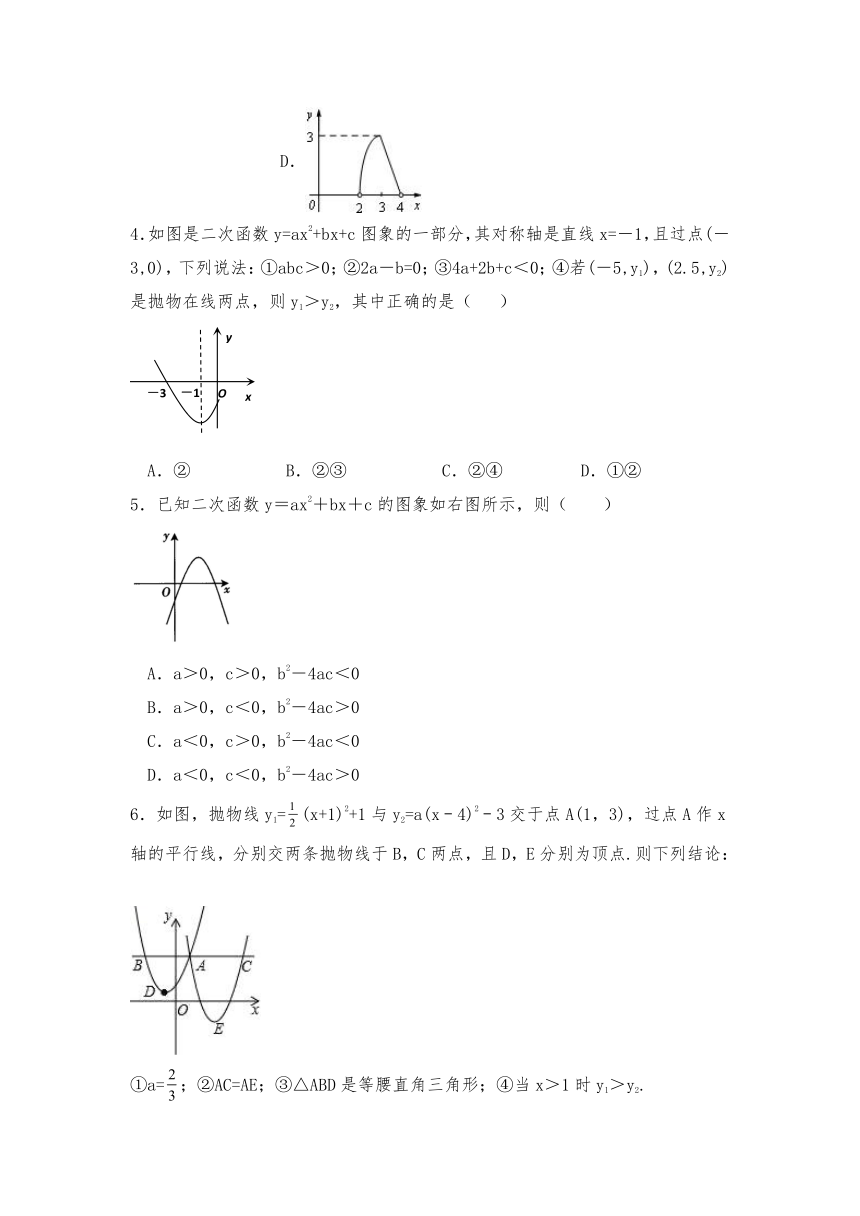



文档简介
1.2二次函数的图象
一、单选题
1.如图,抛物线与轴交于点,顶点坐标,与轴的交点在,之间(包含端点),则下列结论:①;②;③对于任意实数,总成立;④关于的方程有两个不相等的实数根.其中结论正确的个数为( )
A.个 B.个 C.个 D.个
2.设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
A.a(x1﹣x2)=d B.a(x2﹣x1)=d C.a(x1﹣x2)2=d D.a(x1+x2)2=d
3.如图,点C在线段AB上,AB=8,AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,CPD 的面积为y. 则下列图象中,能表示y与x的函数关系的图象大致是( )
A.B.C. D.
4.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc>0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(2.5,y2)是抛物在线两点,则y1>y2,其中正确的是( )
A.② B.②③ C.②④ D.①②
5.已知二次函数y=ax2+bx+c的图象如右图所示,则( )
A.a>0,c>0,b2-4ac<0
B.a>0,c<0,b2-4ac>0
C.a<0,c>0,b2-4ac<0
D.a<0,c<0,b2-4ac>0
6.如图,抛物线y1=(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:
①a=;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
其中正确的结论是( )
A.①③④ B.①③ C.①②④ D.②
7.二次函数 y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①ac>0;②当x≥1时,y随x的增大而减小;③2a+b=0;④b2-4ac<0;⑤4a-2b+c>0,其中正确的个数是( )
A.1 B.2 C.3 D.4
8.方程的解的个数是( )
A.0 B.1 C.2 D.3
二、填空题
9.已知函数,若使y=k成立的x值恰好有三个,则k的值为_______.
10. 二次函数y=x2的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2017在y轴的正半轴上,点B1,B2,B3,…,B2017在二次函数y=x2位于第一象限的图象上.若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2016B2017A2017都为正三角形,则△A2016B2017A2017的边长为____.
(第10题)
11.已知二次函数的图象如图所示,有下列个结论:
①;②;③;④,(的实数); ⑤,其中正确的结论有________.
12.平面直角坐标系中,C(0,4),A为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点A在x轴上运动时,OB+BC的最小值为_____.
13.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
14.如图,抛物线与交于点,过点作轴的平行线,分别交两条抛物线于点,.则以下结论:①无论取何值,2的值总是正数;②;③当时,;④.其中正确结论是___________________.
15.已知点在抛物线上,当时,总有成立,则的取值范围是________.
16.对于3个数:,用表示这三个数的中位数,用表示这三个数的最大数.例如:.如果,则=______________.
三、解答题
17.定义一种变换:平移抛物线F1得到抛物线F2,使F2经过F1的顶点A.设F2的对称轴分别交F1,F2于点D,B,点C是点A关于直线BD的对称点.
(1)如图1,若F1:y=x2,经过变换后,得到F2:y=x2+bx,点C的坐标为(2,0),则:
①b的值等于 ;
②四边形ABCD为( )
A、平行四边形;B、矩形;C、菱形;D、正方形.
(2)如图2,若F1:y=ax2+c,经过变换后,点B的坐标为(2,c﹣1),求△ABD的面积;
(3)如图3,若F1:y=x2﹣x+,经过变换后,AC=2,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
18.在学习函数的过程中,我们经历了通过列表,描点,连线来画函数图象,观察分析图象特征,从而概括出函数的性质的过程.下面是研究函数,性质及其应用的部分过程.请按要求完成下列各小题.
列表:
x … 0 2 3 …
y … 4 a 0 1 2 1 b …
(1)请求出表中a,b的值,并在图中补全该函数的图象;
(2)根据函数图象,写出该函数的一条性质;
(3)已知函数的图象如图所示,结合你所画的函数图象,请直接写出不等式的解集.
19.如图,在平面直角坐标系xoy中,直线与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是,且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;
②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
20.某校九年级数学兴趣社团的同学们学习二次函数后,有兴趣的在一起探究“函数的有关图象和性质”.探究过程如下:
(1)列表:问______.
x … 0 1 2 …
y … 6 2 0 0 0 2 m …
(2)请在平面直角坐标系中画出图象.
(3)若方程(p为常数)有三个实数根,则______.
(4)试写出方程(p为常数)有两个实数根时,p的取值范围是______.
21.如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽(a)”,中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:S△ABC=ah,即三角形的面积等于水平宽与铅垂高乘积的一半.
解答问题:
如图2,顶点为C(1,4)的抛物线y=ax2+bx+c交x轴于点A(3,0)、交y轴于点B.
(1)求抛物线和直线AB的解析式.
(2)点P是抛物线(在第一象限内)上的一个动点,连接PA、PB.
①当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB.
②是否存一点P,使S△PAB=S△CAB?若存在,求出点P的坐标;若不存在,请说明理由.
22.判断下列二次函数的图象与x轴有无交点,若有请求出交点坐标;若无请说明理由.
(1)y=-6x
(2)y=2x2-12x+18.
23.如图,若抛物线的顶点在抛物线上,抛物线的顶点也在抛物线上(点与点不重合),我们定义:这样的两条抛物,互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图,已知抛物线与轴交于点,试求出点关于该抛物线对称轴对称的点的坐标;
(2)请求出以点为顶点的的友好抛物线的解析式,并指出与中同时随增大而增大的自变量的取值范围;
(3)若抛物的任意一条友好抛物线的解析式为,请写出与的关系式,并说明理由.
24.阅读材料:如图1,在平面直角坐标系中,A.B两点的坐标分别为A(,B,AB中点P的坐标为.由,得,同理,所以AB的中点坐标为(,).由勾股定理得,所以A、B两点间的距离公式为AB=.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
如图2,直线l:与抛物线交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
(1)求A、B两点的坐标及P、C两点的坐标;
(2)连结AB、AC,求证:△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
25.已知抛物线与轴交于点,其关于轴对称的抛物线为:,且经过点和点.
(1)求抛物线的解析式;
(2)将抛物线沿轴向右平移得到抛物线,抛物线与轴的交点记为点和点(在的右侧),与轴交于点,如果满足与相似,请求出平移后抛物线的表达式.
答案
一、单选题
C.B.B.C.D.B.B.B.
二、填空题
9.3.
10.2017.
11.①③④⑤
12.4+4.
13.,.
14.①④.
15..
16.或.
三、解答题
17.
解:(1)﹣2;D;
(2)∵F2:y=a(x﹣2)2+c﹣1,
而A(0,c)在F2上,可得a=.
∴DB=(4a+c)﹣(c﹣1)=2,
∴S△ABD=2;
(3)当点C在点A的右侧时(如图1),
设AC与BD交于点N,
抛物线y=x2﹣x+,配方得y=(x﹣1)2+2,
其顶点坐标是A(1,2),
∵AC=2,
∴点C的坐标为(1+2,2).
∵F2过点A,
∴F2解析式为y=(x﹣1﹣)2+1,
∴B(1+,1),
∴D(1+,3)
∴NB=ND=1,
∵点A与点C关于直线BD对称,
∴AC⊥DB,且AN=NC
∴四边形ABCD是菱形.
∴PD=PB.
作PH⊥AD交AD于点H,则PD+PH=PB+PH.
要使PD+PH最小,即要使PB+PH最小,
此最小值是点B到AD的距离,即△ABD边AD上的高h.
∵DN=1,AN=,DB⊥AC,
∴∠DAN=30°,
故△ABD是等边三角形.
∴h=AD=
∴最小值为.
当点C在点A的左侧时(如图2),同理,最小值为.
综上,点P到点D的距离和到直线AD的距离之和的最小值为.
18.
(1)当时,;
当时,;
故;
补全图象如图;
(2)当,或时,y随x的增大而减小;
当时,y随x的增大而增大;(任写一条即可)
(3)由图可知,与所画函数的交点横坐标大于0,
,
解得:,
经检验是原方程的根,
故两个交点为:,
由函数图象可知,
当或时,在所画函数图象上方,
即的解集为或.
19.(1)①y=x+2当x=0时,y=2,当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-对称,
∴点B的坐标为(1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=-
∴y=-x2-x+2.
(2)设P(m,-m2-m+2).
过点P作PQ⊥x轴交AC于点Q,
∴Q(m,m+2),
∴PQ=-m2-m+2-(m+2)
=-m2-2m,
∵S△PAC=×PQ×4,
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).
20.(1)当x=时,
=
=,
∴;
(2)画图象如下;
(3)当x≥0时,函数为;当x<0时,函数为;
∵方程(p为常数)有三个实数根,
∴两个方程有一个公共根,设这个根为a,
则,
解得a=0,
当a=0时,p=0,
故答案为:p=0;
(4)∵方程(p为常数)有两个实数根,
∴p>0;
或△=0
即1+4p=0,
解得.
综上所述,p的取值范围是或.
21.(1)设抛物线的解析式为:y1=a(x-1)2+4,
把A(3,0)代入解析式求得a=-1,
故y1=-(x-1)2+4=-x2+2x+3;
设直线AB的解析式为:y2=kx+b,
求得B点的坐标为(0,3),
把A(3,0),B(0,3)代入y2=kx+b中,
解得:k=-1,b=3,
所以y2=-x+3;
(2)①∵C点坐标为(1,4),
∴当x=1时,y1=4,y2=2
∴CD=4-2=2,
S△CAB=×3×2=3;
②∵C点坐标为(1,4),
∴当x=1时,y1=4,y2=2,
∴CD=4-2=2,
S△CAB=×3×2=3,
假设存在符合条件的点P,设点P的横坐标是x,△PAB的铅垂高为h,
则h=y1-y2=(-x2+2x+3)-(-x+3)=-x2+3x,
由S△PAB=S△CAB,
得:×3×(-x2+3x)=3
化简得:x2-3x+2=0,
∴x=1(舍去)或x=2,
∴点P(2,3).
22.(1)∵a=,b=-6,c=0,
∴b2-4ac=36>0,
∴二次函数的图象与x轴有两个交点.
令y=0,则x2-6x=0,
解得:x=0或9.
则与x轴的交点是(0,0)和(9,0);
(2)∵a=2,b=-12,c=18,
∴b2-4ac=(-12)2-4×2×18=0,
∴二次函数与x轴只有一个交点.
令y=0,则2x2-12x+18=0,
解得:x=3,
则与x轴的交点是(3,0).
23.(1)∵抛物线L3:y=2x2﹣8x+4,∴y=2(x﹣2)2﹣4,∴顶点为(2,-4),对称轴为x=2,设x=0,则y=4,∴C(0,4),∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,4);
(2)∵以点D(4,4)为顶点的L3的友好抛物线L4还过点(2,﹣4),∴L4的解析式为y=﹣2(x﹣4)2+4,由图象可知,当2≤x≤4时,抛物线L3与L4中y同时随x增大而增大;
(3)a1与a2的关系式为a1+a2=0.
理由如下:
∵抛物线y=a1 (x﹣m)2+n的一条“友好”抛物线的解析式为y=a2 (x﹣h)2+k,∴y=a2 (x﹣h)2+k过点(m,n),且y=a1 (x﹣m)2+n过点(h,k),即
k=a1 (h﹣m)2+n…①
n=a2 (m﹣h)2+k…②
由①+②得:(a1+a2)(h﹣m)2=0.
又“友好”抛物线的顶点不重合,∴h≠m,∴a1+a2=0.
24.(1)由,解得:,,则A,B两点的坐标分别为:A(,),B(,),∵P是A,B的中点,由中点坐标公式得P点坐标为(,),即(,3),又∵PC⊥x轴交抛物线于C点,将代入中得,∴C点坐标为(,);
(2)由两点间距离公式得:AB==5,PC=,∴PC=PA=PB,∴∠PAC=∠PCA,∠PBC=∠PCB,∴∠PAC+∠PCB=90°,即∠ACB=90°,∴△ABC为直角三角形;
(3)过点C作CG⊥AB于G,过点A作AH⊥PC于H,则H点的坐标为(,),∴S△PAC=AP CG=PC AH,∴CG=AH=.又∵直线l与l′之间的距离等于点C到l的距离CG,∴直线l与l′之间的距离为.
25.解:(1)抛物线和抛物线关于轴对称,且:,
: ,
经过点和点,
经过点和点,
把点和点代入:可得:
,
解得:,
:;
(2)设抛物线沿轴向右平移个单位得到抛物线,
:,
的解析式可以表示为:
,
抛物线与轴的交点为点和点,且在的右侧,
,
抛物线与轴交于点,
,
∵A(-3,0),C(0,3),
∴△AOC为等腰直角三角形,
∴当△AOC和△DOQ相似时,
△DOQ为等腰直角三角形,
∴OQ=OD,
当点Q在y轴正半轴上时,
OQ=OD=OA=OC,
∴,
解得:a=0(舍)或2,
此时:;
当点Q在y轴负半轴时,
OD=OQ,
则,
解得:a=-1(舍)或4,
此时:;
综上:平移后抛物线W3的表达式为:或.
一、单选题
1.如图,抛物线与轴交于点,顶点坐标,与轴的交点在,之间(包含端点),则下列结论:①;②;③对于任意实数,总成立;④关于的方程有两个不相等的实数根.其中结论正确的个数为( )
A.个 B.个 C.个 D.个
2.设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
A.a(x1﹣x2)=d B.a(x2﹣x1)=d C.a(x1﹣x2)2=d D.a(x1+x2)2=d
3.如图,点C在线段AB上,AB=8,AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,CPD 的面积为y. 则下列图象中,能表示y与x的函数关系的图象大致是( )
A.B.C. D.
4.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc>0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(2.5,y2)是抛物在线两点,则y1>y2,其中正确的是( )
A.② B.②③ C.②④ D.①②
5.已知二次函数y=ax2+bx+c的图象如右图所示,则( )
A.a>0,c>0,b2-4ac<0
B.a>0,c<0,b2-4ac>0
C.a<0,c>0,b2-4ac<0
D.a<0,c<0,b2-4ac>0
6.如图,抛物线y1=(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:
①a=;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
其中正确的结论是( )
A.①③④ B.①③ C.①②④ D.②
7.二次函数 y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①ac>0;②当x≥1时,y随x的增大而减小;③2a+b=0;④b2-4ac<0;⑤4a-2b+c>0,其中正确的个数是( )
A.1 B.2 C.3 D.4
8.方程的解的个数是( )
A.0 B.1 C.2 D.3
二、填空题
9.已知函数,若使y=k成立的x值恰好有三个,则k的值为_______.
10. 二次函数y=x2的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2017在y轴的正半轴上,点B1,B2,B3,…,B2017在二次函数y=x2位于第一象限的图象上.若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2016B2017A2017都为正三角形,则△A2016B2017A2017的边长为____.
(第10题)
11.已知二次函数的图象如图所示,有下列个结论:
①;②;③;④,(的实数); ⑤,其中正确的结论有________.
12.平面直角坐标系中,C(0,4),A为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点A在x轴上运动时,OB+BC的最小值为_____.
13.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
14.如图,抛物线与交于点,过点作轴的平行线,分别交两条抛物线于点,.则以下结论:①无论取何值,2的值总是正数;②;③当时,;④.其中正确结论是___________________.
15.已知点在抛物线上,当时,总有成立,则的取值范围是________.
16.对于3个数:,用表示这三个数的中位数,用表示这三个数的最大数.例如:.如果,则=______________.
三、解答题
17.定义一种变换:平移抛物线F1得到抛物线F2,使F2经过F1的顶点A.设F2的对称轴分别交F1,F2于点D,B,点C是点A关于直线BD的对称点.
(1)如图1,若F1:y=x2,经过变换后,得到F2:y=x2+bx,点C的坐标为(2,0),则:
①b的值等于 ;
②四边形ABCD为( )
A、平行四边形;B、矩形;C、菱形;D、正方形.
(2)如图2,若F1:y=ax2+c,经过变换后,点B的坐标为(2,c﹣1),求△ABD的面积;
(3)如图3,若F1:y=x2﹣x+,经过变换后,AC=2,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
18.在学习函数的过程中,我们经历了通过列表,描点,连线来画函数图象,观察分析图象特征,从而概括出函数的性质的过程.下面是研究函数,性质及其应用的部分过程.请按要求完成下列各小题.
列表:
x … 0 2 3 …
y … 4 a 0 1 2 1 b …
(1)请求出表中a,b的值,并在图中补全该函数的图象;
(2)根据函数图象,写出该函数的一条性质;
(3)已知函数的图象如图所示,结合你所画的函数图象,请直接写出不等式的解集.
19.如图,在平面直角坐标系xoy中,直线与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是,且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;
②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
20.某校九年级数学兴趣社团的同学们学习二次函数后,有兴趣的在一起探究“函数的有关图象和性质”.探究过程如下:
(1)列表:问______.
x … 0 1 2 …
y … 6 2 0 0 0 2 m …
(2)请在平面直角坐标系中画出图象.
(3)若方程(p为常数)有三个实数根,则______.
(4)试写出方程(p为常数)有两个实数根时,p的取值范围是______.
21.如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽(a)”,中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:S△ABC=ah,即三角形的面积等于水平宽与铅垂高乘积的一半.
解答问题:
如图2,顶点为C(1,4)的抛物线y=ax2+bx+c交x轴于点A(3,0)、交y轴于点B.
(1)求抛物线和直线AB的解析式.
(2)点P是抛物线(在第一象限内)上的一个动点,连接PA、PB.
①当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB.
②是否存一点P,使S△PAB=S△CAB?若存在,求出点P的坐标;若不存在,请说明理由.
22.判断下列二次函数的图象与x轴有无交点,若有请求出交点坐标;若无请说明理由.
(1)y=-6x
(2)y=2x2-12x+18.
23.如图,若抛物线的顶点在抛物线上,抛物线的顶点也在抛物线上(点与点不重合),我们定义:这样的两条抛物,互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图,已知抛物线与轴交于点,试求出点关于该抛物线对称轴对称的点的坐标;
(2)请求出以点为顶点的的友好抛物线的解析式,并指出与中同时随增大而增大的自变量的取值范围;
(3)若抛物的任意一条友好抛物线的解析式为,请写出与的关系式,并说明理由.
24.阅读材料:如图1,在平面直角坐标系中,A.B两点的坐标分别为A(,B,AB中点P的坐标为.由,得,同理,所以AB的中点坐标为(,).由勾股定理得,所以A、B两点间的距离公式为AB=.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
如图2,直线l:与抛物线交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
(1)求A、B两点的坐标及P、C两点的坐标;
(2)连结AB、AC,求证:△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
25.已知抛物线与轴交于点,其关于轴对称的抛物线为:,且经过点和点.
(1)求抛物线的解析式;
(2)将抛物线沿轴向右平移得到抛物线,抛物线与轴的交点记为点和点(在的右侧),与轴交于点,如果满足与相似,请求出平移后抛物线的表达式.
答案
一、单选题
C.B.B.C.D.B.B.B.
二、填空题
9.3.
10.2017.
11.①③④⑤
12.4+4.
13.,.
14.①④.
15..
16.或.
三、解答题
17.
解:(1)﹣2;D;
(2)∵F2:y=a(x﹣2)2+c﹣1,
而A(0,c)在F2上,可得a=.
∴DB=(4a+c)﹣(c﹣1)=2,
∴S△ABD=2;
(3)当点C在点A的右侧时(如图1),
设AC与BD交于点N,
抛物线y=x2﹣x+,配方得y=(x﹣1)2+2,
其顶点坐标是A(1,2),
∵AC=2,
∴点C的坐标为(1+2,2).
∵F2过点A,
∴F2解析式为y=(x﹣1﹣)2+1,
∴B(1+,1),
∴D(1+,3)
∴NB=ND=1,
∵点A与点C关于直线BD对称,
∴AC⊥DB,且AN=NC
∴四边形ABCD是菱形.
∴PD=PB.
作PH⊥AD交AD于点H,则PD+PH=PB+PH.
要使PD+PH最小,即要使PB+PH最小,
此最小值是点B到AD的距离,即△ABD边AD上的高h.
∵DN=1,AN=,DB⊥AC,
∴∠DAN=30°,
故△ABD是等边三角形.
∴h=AD=
∴最小值为.
当点C在点A的左侧时(如图2),同理,最小值为.
综上,点P到点D的距离和到直线AD的距离之和的最小值为.
18.
(1)当时,;
当时,;
故;
补全图象如图;
(2)当,或时,y随x的增大而减小;
当时,y随x的增大而增大;(任写一条即可)
(3)由图可知,与所画函数的交点横坐标大于0,
,
解得:,
经检验是原方程的根,
故两个交点为:,
由函数图象可知,
当或时,在所画函数图象上方,
即的解集为或.
19.(1)①y=x+2当x=0时,y=2,当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-对称,
∴点B的坐标为(1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=-
∴y=-x2-x+2.
(2)设P(m,-m2-m+2).
过点P作PQ⊥x轴交AC于点Q,
∴Q(m,m+2),
∴PQ=-m2-m+2-(m+2)
=-m2-2m,
∵S△PAC=×PQ×4,
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).
20.(1)当x=时,
=
=,
∴;
(2)画图象如下;
(3)当x≥0时,函数为;当x<0时,函数为;
∵方程(p为常数)有三个实数根,
∴两个方程有一个公共根,设这个根为a,
则,
解得a=0,
当a=0时,p=0,
故答案为:p=0;
(4)∵方程(p为常数)有两个实数根,
∴p>0;
或△=0
即1+4p=0,
解得.
综上所述,p的取值范围是或.
21.(1)设抛物线的解析式为:y1=a(x-1)2+4,
把A(3,0)代入解析式求得a=-1,
故y1=-(x-1)2+4=-x2+2x+3;
设直线AB的解析式为:y2=kx+b,
求得B点的坐标为(0,3),
把A(3,0),B(0,3)代入y2=kx+b中,
解得:k=-1,b=3,
所以y2=-x+3;
(2)①∵C点坐标为(1,4),
∴当x=1时,y1=4,y2=2
∴CD=4-2=2,
S△CAB=×3×2=3;
②∵C点坐标为(1,4),
∴当x=1时,y1=4,y2=2,
∴CD=4-2=2,
S△CAB=×3×2=3,
假设存在符合条件的点P,设点P的横坐标是x,△PAB的铅垂高为h,
则h=y1-y2=(-x2+2x+3)-(-x+3)=-x2+3x,
由S△PAB=S△CAB,
得:×3×(-x2+3x)=3
化简得:x2-3x+2=0,
∴x=1(舍去)或x=2,
∴点P(2,3).
22.(1)∵a=,b=-6,c=0,
∴b2-4ac=36>0,
∴二次函数的图象与x轴有两个交点.
令y=0,则x2-6x=0,
解得:x=0或9.
则与x轴的交点是(0,0)和(9,0);
(2)∵a=2,b=-12,c=18,
∴b2-4ac=(-12)2-4×2×18=0,
∴二次函数与x轴只有一个交点.
令y=0,则2x2-12x+18=0,
解得:x=3,
则与x轴的交点是(3,0).
23.(1)∵抛物线L3:y=2x2﹣8x+4,∴y=2(x﹣2)2﹣4,∴顶点为(2,-4),对称轴为x=2,设x=0,则y=4,∴C(0,4),∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,4);
(2)∵以点D(4,4)为顶点的L3的友好抛物线L4还过点(2,﹣4),∴L4的解析式为y=﹣2(x﹣4)2+4,由图象可知,当2≤x≤4时,抛物线L3与L4中y同时随x增大而增大;
(3)a1与a2的关系式为a1+a2=0.
理由如下:
∵抛物线y=a1 (x﹣m)2+n的一条“友好”抛物线的解析式为y=a2 (x﹣h)2+k,∴y=a2 (x﹣h)2+k过点(m,n),且y=a1 (x﹣m)2+n过点(h,k),即
k=a1 (h﹣m)2+n…①
n=a2 (m﹣h)2+k…②
由①+②得:(a1+a2)(h﹣m)2=0.
又“友好”抛物线的顶点不重合,∴h≠m,∴a1+a2=0.
24.(1)由,解得:,,则A,B两点的坐标分别为:A(,),B(,),∵P是A,B的中点,由中点坐标公式得P点坐标为(,),即(,3),又∵PC⊥x轴交抛物线于C点,将代入中得,∴C点坐标为(,);
(2)由两点间距离公式得:AB==5,PC=,∴PC=PA=PB,∴∠PAC=∠PCA,∠PBC=∠PCB,∴∠PAC+∠PCB=90°,即∠ACB=90°,∴△ABC为直角三角形;
(3)过点C作CG⊥AB于G,过点A作AH⊥PC于H,则H点的坐标为(,),∴S△PAC=AP CG=PC AH,∴CG=AH=.又∵直线l与l′之间的距离等于点C到l的距离CG,∴直线l与l′之间的距离为.
25.解:(1)抛物线和抛物线关于轴对称,且:,
: ,
经过点和点,
经过点和点,
把点和点代入:可得:
,
解得:,
:;
(2)设抛物线沿轴向右平移个单位得到抛物线,
:,
的解析式可以表示为:
,
抛物线与轴的交点为点和点,且在的右侧,
,
抛物线与轴交于点,
,
∵A(-3,0),C(0,3),
∴△AOC为等腰直角三角形,
∴当△AOC和△DOQ相似时,
△DOQ为等腰直角三角形,
∴OQ=OD,
当点Q在y轴正半轴上时,
OQ=OD=OA=OC,
∴,
解得:a=0(舍)或2,
此时:;
当点Q在y轴负半轴时,
OD=OQ,
则,
解得:a=-1(舍)或4,
此时:;
综上:平移后抛物线W3的表达式为:或.
同课章节目录
