浙教版九年级数学上册试题 4.4两个三角形相似的判定 同步练习(含答案)
文档属性
| 名称 | 浙教版九年级数学上册试题 4.4两个三角形相似的判定 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 10:44:05 | ||
图片预览




文档简介
4.4两个相似三角形的判定
一、单选题
1.如图,在 ABCD中,E在AB上,CE、BD交于F,若AE::3,且,则DF的长为
A. B. C. D.
2.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1 B.2 C.3 D.4
3.如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上,则CE:CF的值为( )
A. B. C. D.
4.如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PE BF;⑤线段MN的最小值为.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
5.如图,点E为 ABCD的AD边上一点,且AE∶ED=1∶3,点F为AB的中点,EF交AC于点G,则AG∶GC等于( )
A.1∶2 B.1∶5 C.1∶4 D.1∶3
6.如图,矩形ABCD中,折叠矩形一边AD,使点D落在BC边的点F处,已知折痕AE=,且CE:CF=3:4,则矩形ABCD的周长为( )
A.36cm B.3 C.72cm D.7
7.如图,在△ABC中,D为AB边上一点,E为CD中点,AC=,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A. B. +1﹣ C.﹣ D.﹣1
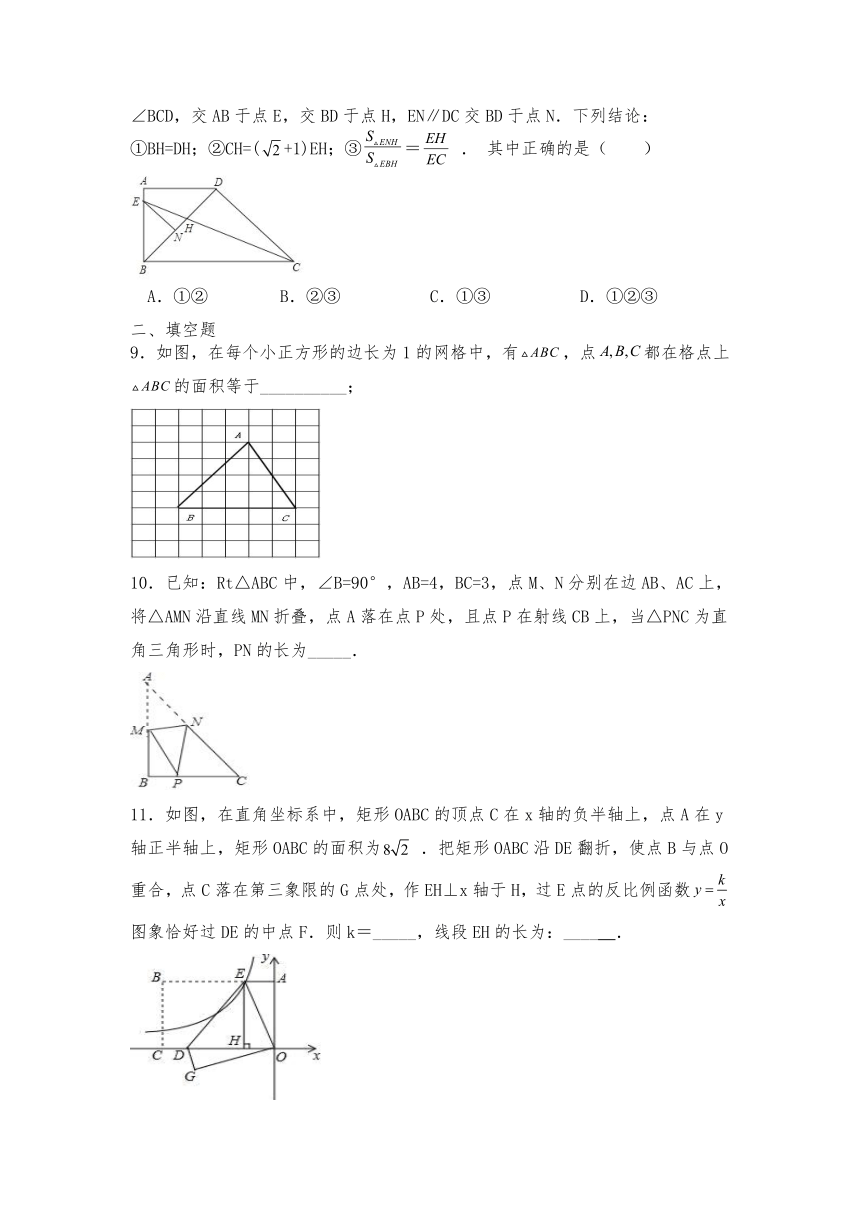
8.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(+1)EH;③= . 其中正确的是( )
A.①② B.②③ C.①③ D.①②③
二、填空题
9.如图,在每个小正方形的边长为1的网格中,有,点都在格点上
的面积等于__________;
10.已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为_____.
11.如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为 .把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数图象恰好过DE的中点F.则k=_____,线段EH的长为:____ .
12.如图,梯形ABCD中,AD∥BC,∠D=90°,BC=CD=12,∠ABE=45°,点E在DC上,AE,BC的延长线相交于点F,若AE=10,则S△ADE+S△CEF的值是______ .
13.在平面直角坐标系中,已知点A、B的坐标分别为(10,0)、(0,4),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C以每秒1个单位匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P运动的时间为_____秒.
14.如图所示,n+1个直角边长为3的等腰直角三角形△AB1C1,△C1B2C2……,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1Dn n的面积为Sn,则S1=_____;S2=_____;Sn=_____.
15.如图,已知 ABCD中,AB=3,BC=5,∠BAC=90°,E、F分别是AB,BC上的动点,EF⊥BC,△BEF与△PEF关于直线EF对称,若△APD是直角三角形,则BF的长为_____.
16.如图,是△的中线,点在边上,且⊥,将△绕着点旋转,使得点与点重合,点落在点处,联结交于点,如果,那么的值等于______.
三、解答题
17.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t;
①当S△ACP=S△ACN时,求点P的坐标;
②是否存在点P,使得△ACP是以AC为斜边的直角三角形?若存在,求点P的坐标;若不存在,请说明理由;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.
18.如图,二次函数图象的顶点为,对称轴是直线,一次函数的图象与轴交于点,且与直线关于的对称直线交于点.
(1)点的坐标是 ______;
(2)直线与直线交于点,是线段上一点(不与点、重合),点的纵坐标为.过点作直线与线段、分别交于点,,使得与相似.
①当时,求的长;
②若对于每一个确定的的值,有且只有一个与相似,请直接写出的取值范围______.
19.如图,已知中,,点以每秒1个单位的速度从向运动,同时点以每秒2个单位的速度从向方向运动,到达点后,点也停止运动,设点运动的时间为秒.
(1)求点停止运动时,的长;
(2) 两点在运动过程中,点是点关于直线的对称点,是否存在时间,使四边形为菱形 若存在,求出此时的值;若不存在,请说明理由.
(3) 两点在运动过程中,求使与相似的时间的值.
20.关于x的方程①和一元二次方程②中,k,m均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当k为最小整数时,方程②有两根分别为和,求m的值;
(3)在(2)的条件下,若直线y=kx+1与x轴,y轴分别交于点A,B,点C是双曲线在第一象限图像上一动点,作CD⊥y轴交线段AB于点E,作CF⊥x轴交线段AB于点G,坐标原点为O.按要求补全图形并完成:
①BG·AE=___________;
②求∠EOG的度数.
21.如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
(1)求证:△AEB∽△CFB;
(2)若CE=5,,BD=6.求AD的长.
22.定义为函数的“特征数”.如:函数的“特征数”是,函数的“特征数”是.
(1)将“特征数”是的函数的图象向下平移2个单位,得到一个新函数图象,求这个新函数图象的解析式;
(2)“特征”是的函数图象与轴分别交点,“特征数”是的函数图象与轴交于点,点是原点,判断与是否相似,请说明理由.
23.如图,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点B坐标为(4,﹣3).把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E.
(1)线段AC= ;
(2)求点D坐标及折痕DE的长;
(3)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请求出点Q的坐标;若不存在,请说明理由.
24.已知△ABC中,AB=AC,∠BAC=90°,点D是平面内一点;
(1)如图1, BD⊥CD,∠DCA=30°,则∠BAD=
(2)如图2,若∠BDC=45°,点F是CD中点,求证:AF⊥CD;
(3)如图3,∠BDA=3∠CBD,BD=,求△BCD的面积.
25.如图,在△ABC 中, AD 是 BC 边上的中线,点 E 是 AD 的中点,过点 A 作AF // BC 交 BE 的延长线于 F ,连接CF .
(1)求证: △AEF △DEB ;
(2)若BAC 90,试判断四边形 ADCF 的形状,并证明你的结论;
(3)在(2)的情况下,如果 AC 2 ,点 M 在 AC 线段上移动,当 MB MD 有最小值时,求 AM 的长度(提示:以 D 点为原点, AD 为 y 正半轴, DC 为 x 正轴建立平面直角坐标系).
26.如图,抛物线与轴交于A、B两点,与轴交于点C,直线过B、C两点,连接AC.
(1)求抛物线的解析式;
(2)求证:;
(3)点是抛物线上的一点,点D为抛物线上位于直线BC上方的一点,过点D作轴交直线BC于点E,点P为抛物线对称轴上一动点,当线段DE的长度最大时,求的最小值.
答案
一、单选题
D.D.A.D.B.C.D.B.
二、填空题
9.;
10.或
11.-2 2
12.30或48.
13.1或4.
14., 3,
15.或
16.
三、解答题
17.
(1)将A(﹣1,0),C(2,3)代入y=﹣x2+bx+c中,得,
解得:,
∴抛物线解析式为y=﹣x2+2x+3,
设直线AC解析式为y=mx+n,
∵点A(-1,0)、C(2,3)在直线AC上,
∴,
解得:,
∴直线AC解析式为y=x+1.
(2)①在y=﹣x2+2x+3中,令x=0,得y=3,
∴N(0,3),
∵点P的横坐标为t,点P在抛物线y=-x2+2x+3图象上,
∴P(t,﹣t2+2t+3),
如图,过点P作PH//AC,
∵平行线间的距离相等,
∴S△ACP=S△CAN,
设直线NP的解析式为y=kx+a,
∴k=1,
把N(0,3)代入得a=3,
∴直线NP的解析式为y=x+3,
联立直线NP与抛物线解析式得,
解得:或(舍去),
∴P(1,4).
②如图2,过P作PS⊥x轴于S,过C作CK⊥PS于K,则∠CKP=∠PSA=90°,
∵P(t,﹣t2+2t+3),A(﹣1,0),C(2,3),
∴CK=2﹣t,PK=﹣t2+2t,PS=﹣t2+2t+3,AS=t﹣(﹣1)=t+1,
∵△ACP是以AC为斜边的直角三角形,
∴∠APS+∠CPK=∠APC=90°,
∵∠PCK+∠CPK=90°,
∴∠APS=∠PCK,
∴△APS∽△PCK,
∴=,即=,
解得:t=,
∵P是抛物线上位于直线AC上方的一个动点,
∴﹣1<t<2,
∵>2,
∴t=,
∴﹣t2+2t+3=,
∴P(,).
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4),
∴B(1,2),BD=2,
∵点E在直线AC上,AC解析式为y=x+1,
∴设点E(m,m+1),
∵B,D,E,F为顶点的四边形为平行四边形,
∴EF=BD,
∵EF//BD,BD为抛物线对称轴,
∴F(m,﹣m2+2m+3),EF=,
∴m2-m-2=±2,解得:m1=0,m2=1(舍去),m3=,m4=,
∴,以B,D,E,F为顶点的四边形能为平行四边形,点E的坐标为:(0,1)或(,)或(,).
18.
(1)顶点为;
故答案为;
(2)对称轴,
,
由已知可求,
点关于对称点为,
则关于对称的直线为,
,
①当时,,
,,
当时,,
,
,
;
当与不平行时,,
,
,
;
综上所述或;
②当,时,
,
,
,
,
∴有且只有一个与相似时,;
故答案为;
19.
(1)在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB==10,
点Q运动到点A时,t==5,
∴AP=5,PC=1,
在Rt△PBC中,PB=.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.
∵四边形PQCE是菱形,
∴PC⊥EQ,PK=KC,
∵∠QKC=∠QDC=∠DCK=90°,
∴四边形QDCK是矩形,
∴DQ=CK,
∴,
解得t=.
∴t=s时,四边形PQCE是菱形.
(3)如图2中,当∠APQ=90°时,
∵∠APQ=∠C=90°,
∴PQ∥BC,
∴,
∴,
∴.
如图3中,当∠AQP=90°时,
∵△AQP∽△ACB,
∴,
∴,
∴,
综上所述,或s时,△APQ是直角三角形.
20.
(1)∵,
∴x=,
∵方程的根为非负数,方程是一元二次方程,
∴≥0,2-k≠0,
解得:k≥-1且k≠2.
(2)由(1)可知k≥-1,
∵k为最小整数,
∴k=-1,
∴方程②为,
∵方程②有两根分别为和,
∴+()=,即-m=-4,
解得:m=4.
(3)①根据题意补全图形如下,过点E作EP⊥x轴于P,过G作GQ⊥y轴于Q,由(2)可知k=-1,m=4,
∴直线AB解析式为y=-x+1,双曲线的解析式为,
∵直线y=kx+1与x轴,y轴分别交于点A,B,
∴A(1,0),B(0,1),
∴OA=OB=1,∠OBA=∠OAB=45°,
∴△AOB是等腰直角三角形,
∵EP⊥x轴,GQ⊥y轴,
∴△BQG和△EPA是等腰直角三角形,
∴BG=GQ,AE=PE,
∵CD⊥y轴,CF⊥x轴,
∴GQ=CD,PE=CF,
设点C坐标为(t,),则CD=t,CF=,
∴BG·AE=t×·=1.
②如图,连接OE、OG,
由①得BG·AE=1,OA=OB=1,∠OBA=∠OAB=45°,
∴BG=,
∴,
∴△BOG∽△AEO,
∴∠OGB=∠EOA,
∵∠OGB=∠GOA+∠OAB,∠EOA=∠EOG+∠GOA,
∴∠EOG=∠OAB=45°.
21.
(1)证明:,
,
为边上的高,
,
,
,
是的平分线,
,
.
(2)解:如图,作于.
∵∠BFD+∠ABE=90°,∠CEB+∠CBE=90°,∠ABE=∠CBE,
∴∠BFD=∠CEB,
∵∠BFD=∠CFE,
,
为等腰三角形,
,
,
∴点为的中点,
,
,
,
,
,
,
,,
,
,
根据,即,
,
,
,
,
.
22.
解:(1)函数的“特征数”是,,,函数的“特征数”是,2,,函数的“特征数”是,,,
“特征数”是,,的函数解析式是:,
函数的图象向下平移2个单位,
;
(2) “特征数”是的函数图象与、轴分别交点、,
函数解析式为:,
图象与、轴分别点、,
“特征数”是的函数图象与轴交于点,
函数解析式为:
图象与、轴分别点、,
,,.
,
又∠DOE=∠COD,
.
23.
解:(1)∵四边形OABC是矩形,点B坐标为(4,﹣3).
∴∠AOC=90°.OA=3,OC=4,
∴AC==5.
故答案为5;
(2)由折叠可得:DE⊥AC,AF=FC=,
∵∠FCD=∠OCA,∠DFC=∠AOC=90°,
∴△DFC∽△AOC.
∴==,
∴==,
∴DF=,DC=,
∴OD=OC﹣DC=4﹣=.
∴D(,0);
∵四边形OABC是矩形,
∴AB∥DC,
∴∠EAF=∠DCF,
在△AFE和△CFD中,,
∴△AFE≌△CFD(ASA).
∴EF=DF.
∴DE=2DF=2×=.
即折痕DE的长为.
(3)如图所示:
由(2)可知,AE=CD=
∴E(,﹣3),D(,0),
①当DE为菱形的边时,DP=DE=,可得Q(,﹣3),Q1(﹣,﹣3).
②当DE为菱形的对角线时,P与C重合,Q与A重合,Q2(0,﹣3),
③当点Q在第一象限,E与Q关于x轴对称,Q(,3)
综上所述,满足条件的点Q坐标为(,﹣3)或(﹣,﹣3)或(0,﹣3)或(,3).
24.
解:(1)∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠DCA=30°,
∴∠BCD=45°-30°=15°,
又∵BD⊥CD,
∴∠CBD=90°-15°=75°,
∴∠ABD=75°-45°=30°,
在Rt△ACE和Rt△BDE中,∠ACE=30°,∠ABD=30°,
∴ , ,
在△CEB和△AED中,
∠CEB=∠AED,,
∴△CEB∽△AED,
∴∠BAD=∠BCD=15°.
(2)如图,作三角形BCD的外接圆,则∠BCD为圆周角,
∵∠BDC=45°,
∴所对的圆心角为90°,
∵∠BAC=90°,
∴点A即为△BCD的外接圆的圆心,
∴AC=AD,
∵点F是CD中点,
∴AF⊥CD.
(3)如图,过点D作DE⊥BC于点E,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠BDA=3∠CBD,∠BDA=∠C+∠CBD,
∴∠C=2∠CBD,
∵∠ABC=∠ACB,∠ABC=∠ABD+∠CBD,
∴∠ABD=∠CBD,
又∵∠BAC=90°,DE⊥BC,
∴DE=AD,
设DE=AD=a,
易得△CED为等腰直角三角形,
∴CD=,
∴AB=AC=,
∵BD=,
∴在Rt△ABD中,,
解得 ,
∴AB=AC=,
∴BC=,
∴ .
25.
(1)∵AF∥BC,∴∠AFE=∠DBE.在△AEF和△DEB中,∵,∴△AEF≌△DEB;
(2)四边形ADCF是菱形,理由如下:
∵△AEF≌△DEB,∴AF=BD.
∵BD=DC,∴AF=DC.
又∵AF∥BC,∴四边形ADCF是平行四边形.
∵∠BAC=90°,AD是BC边上的中线,∴AD=DC,∴四边形ADCF是菱形;
(3)连接BF交AC于M,则点M即为所求.
∵四边形ADCF是菱形,∴点D与点F关于直线AC对称,∴MD=MF,∴MB+MD=MB+MF=BF,即MB+MD有最小值.
∵AF=DC=BD,∴BC=2AF.
∵AF∥BC,∴△AMF∽△CMB,∴,∴,∴AM=AC.
∵AC=2,∴AM=.
26.
(1)解:∵直线分别与轴和轴交于点B和点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
把,分别代入,
得,
解得,
∴抛物线的解析式为.
(2)∵抛物线与x轴交于点A,
∴,
解得,,
∴点A的坐标为,
∴,,
在中,,,
∴,
∴,
∵,
∴,
又∵,
∴.
(3)设点D的坐标为
则点E的坐标为
∴
=
∵,
∴当时,线段DE的长度最大.
此时,点D的坐标为,
∵,
∴点C和点M关于对称轴对称,
连接CD交对称轴于点P,此时最小.
连接CM交直线DE于点F,则,点F的坐标为,
∴,
∵
∴的最小值.
.
一、单选题
1.如图,在 ABCD中,E在AB上,CE、BD交于F,若AE::3,且,则DF的长为
A. B. C. D.
2.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1 B.2 C.3 D.4
3.如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上,则CE:CF的值为( )
A. B. C. D.
4.如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PE BF;⑤线段MN的最小值为.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
5.如图,点E为 ABCD的AD边上一点,且AE∶ED=1∶3,点F为AB的中点,EF交AC于点G,则AG∶GC等于( )
A.1∶2 B.1∶5 C.1∶4 D.1∶3
6.如图,矩形ABCD中,折叠矩形一边AD,使点D落在BC边的点F处,已知折痕AE=,且CE:CF=3:4,则矩形ABCD的周长为( )
A.36cm B.3 C.72cm D.7
7.如图,在△ABC中,D为AB边上一点,E为CD中点,AC=,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A. B. +1﹣ C.﹣ D.﹣1
8.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(+1)EH;③= . 其中正确的是( )
A.①② B.②③ C.①③ D.①②③
二、填空题
9.如图,在每个小正方形的边长为1的网格中,有,点都在格点上
的面积等于__________;
10.已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为_____.
11.如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为 .把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数图象恰好过DE的中点F.则k=_____,线段EH的长为:____ .
12.如图,梯形ABCD中,AD∥BC,∠D=90°,BC=CD=12,∠ABE=45°,点E在DC上,AE,BC的延长线相交于点F,若AE=10,则S△ADE+S△CEF的值是______ .
13.在平面直角坐标系中,已知点A、B的坐标分别为(10,0)、(0,4),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C以每秒1个单位匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P运动的时间为_____秒.
14.如图所示,n+1个直角边长为3的等腰直角三角形△AB1C1,△C1B2C2……,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1Dn n的面积为Sn,则S1=_____;S2=_____;Sn=_____.
15.如图,已知 ABCD中,AB=3,BC=5,∠BAC=90°,E、F分别是AB,BC上的动点,EF⊥BC,△BEF与△PEF关于直线EF对称,若△APD是直角三角形,则BF的长为_____.
16.如图,是△的中线,点在边上,且⊥,将△绕着点旋转,使得点与点重合,点落在点处,联结交于点,如果,那么的值等于______.
三、解答题
17.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t;
①当S△ACP=S△ACN时,求点P的坐标;
②是否存在点P,使得△ACP是以AC为斜边的直角三角形?若存在,求点P的坐标;若不存在,请说明理由;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.
18.如图,二次函数图象的顶点为,对称轴是直线,一次函数的图象与轴交于点,且与直线关于的对称直线交于点.
(1)点的坐标是 ______;
(2)直线与直线交于点,是线段上一点(不与点、重合),点的纵坐标为.过点作直线与线段、分别交于点,,使得与相似.
①当时,求的长;
②若对于每一个确定的的值,有且只有一个与相似,请直接写出的取值范围______.
19.如图,已知中,,点以每秒1个单位的速度从向运动,同时点以每秒2个单位的速度从向方向运动,到达点后,点也停止运动,设点运动的时间为秒.
(1)求点停止运动时,的长;
(2) 两点在运动过程中,点是点关于直线的对称点,是否存在时间,使四边形为菱形 若存在,求出此时的值;若不存在,请说明理由.
(3) 两点在运动过程中,求使与相似的时间的值.
20.关于x的方程①和一元二次方程②中,k,m均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当k为最小整数时,方程②有两根分别为和,求m的值;
(3)在(2)的条件下,若直线y=kx+1与x轴,y轴分别交于点A,B,点C是双曲线在第一象限图像上一动点,作CD⊥y轴交线段AB于点E,作CF⊥x轴交线段AB于点G,坐标原点为O.按要求补全图形并完成:
①BG·AE=___________;
②求∠EOG的度数.
21.如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
(1)求证:△AEB∽△CFB;
(2)若CE=5,,BD=6.求AD的长.
22.定义为函数的“特征数”.如:函数的“特征数”是,函数的“特征数”是.
(1)将“特征数”是的函数的图象向下平移2个单位,得到一个新函数图象,求这个新函数图象的解析式;
(2)“特征”是的函数图象与轴分别交点,“特征数”是的函数图象与轴交于点,点是原点,判断与是否相似,请说明理由.
23.如图,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点B坐标为(4,﹣3).把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E.
(1)线段AC= ;
(2)求点D坐标及折痕DE的长;
(3)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请求出点Q的坐标;若不存在,请说明理由.
24.已知△ABC中,AB=AC,∠BAC=90°,点D是平面内一点;
(1)如图1, BD⊥CD,∠DCA=30°,则∠BAD=
(2)如图2,若∠BDC=45°,点F是CD中点,求证:AF⊥CD;
(3)如图3,∠BDA=3∠CBD,BD=,求△BCD的面积.
25.如图,在△ABC 中, AD 是 BC 边上的中线,点 E 是 AD 的中点,过点 A 作AF // BC 交 BE 的延长线于 F ,连接CF .
(1)求证: △AEF △DEB ;
(2)若BAC 90,试判断四边形 ADCF 的形状,并证明你的结论;
(3)在(2)的情况下,如果 AC 2 ,点 M 在 AC 线段上移动,当 MB MD 有最小值时,求 AM 的长度(提示:以 D 点为原点, AD 为 y 正半轴, DC 为 x 正轴建立平面直角坐标系).
26.如图,抛物线与轴交于A、B两点,与轴交于点C,直线过B、C两点,连接AC.
(1)求抛物线的解析式;
(2)求证:;
(3)点是抛物线上的一点,点D为抛物线上位于直线BC上方的一点,过点D作轴交直线BC于点E,点P为抛物线对称轴上一动点,当线段DE的长度最大时,求的最小值.
答案
一、单选题
D.D.A.D.B.C.D.B.
二、填空题
9.;
10.或
11.-2 2
12.30或48.
13.1或4.
14., 3,
15.或
16.
三、解答题
17.
(1)将A(﹣1,0),C(2,3)代入y=﹣x2+bx+c中,得,
解得:,
∴抛物线解析式为y=﹣x2+2x+3,
设直线AC解析式为y=mx+n,
∵点A(-1,0)、C(2,3)在直线AC上,
∴,
解得:,
∴直线AC解析式为y=x+1.
(2)①在y=﹣x2+2x+3中,令x=0,得y=3,
∴N(0,3),
∵点P的横坐标为t,点P在抛物线y=-x2+2x+3图象上,
∴P(t,﹣t2+2t+3),
如图,过点P作PH//AC,
∵平行线间的距离相等,
∴S△ACP=S△CAN,
设直线NP的解析式为y=kx+a,
∴k=1,
把N(0,3)代入得a=3,
∴直线NP的解析式为y=x+3,
联立直线NP与抛物线解析式得,
解得:或(舍去),
∴P(1,4).
②如图2,过P作PS⊥x轴于S,过C作CK⊥PS于K,则∠CKP=∠PSA=90°,
∵P(t,﹣t2+2t+3),A(﹣1,0),C(2,3),
∴CK=2﹣t,PK=﹣t2+2t,PS=﹣t2+2t+3,AS=t﹣(﹣1)=t+1,
∵△ACP是以AC为斜边的直角三角形,
∴∠APS+∠CPK=∠APC=90°,
∵∠PCK+∠CPK=90°,
∴∠APS=∠PCK,
∴△APS∽△PCK,
∴=,即=,
解得:t=,
∵P是抛物线上位于直线AC上方的一个动点,
∴﹣1<t<2,
∵>2,
∴t=,
∴﹣t2+2t+3=,
∴P(,).
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4),
∴B(1,2),BD=2,
∵点E在直线AC上,AC解析式为y=x+1,
∴设点E(m,m+1),
∵B,D,E,F为顶点的四边形为平行四边形,
∴EF=BD,
∵EF//BD,BD为抛物线对称轴,
∴F(m,﹣m2+2m+3),EF=,
∴m2-m-2=±2,解得:m1=0,m2=1(舍去),m3=,m4=,
∴,以B,D,E,F为顶点的四边形能为平行四边形,点E的坐标为:(0,1)或(,)或(,).
18.
(1)顶点为;
故答案为;
(2)对称轴,
,
由已知可求,
点关于对称点为,
则关于对称的直线为,
,
①当时,,
,,
当时,,
,
,
;
当与不平行时,,
,
,
;
综上所述或;
②当,时,
,
,
,
,
∴有且只有一个与相似时,;
故答案为;
19.
(1)在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB==10,
点Q运动到点A时,t==5,
∴AP=5,PC=1,
在Rt△PBC中,PB=.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.
∵四边形PQCE是菱形,
∴PC⊥EQ,PK=KC,
∵∠QKC=∠QDC=∠DCK=90°,
∴四边形QDCK是矩形,
∴DQ=CK,
∴,
解得t=.
∴t=s时,四边形PQCE是菱形.
(3)如图2中,当∠APQ=90°时,
∵∠APQ=∠C=90°,
∴PQ∥BC,
∴,
∴,
∴.
如图3中,当∠AQP=90°时,
∵△AQP∽△ACB,
∴,
∴,
∴,
综上所述,或s时,△APQ是直角三角形.
20.
(1)∵,
∴x=,
∵方程的根为非负数,方程是一元二次方程,
∴≥0,2-k≠0,
解得:k≥-1且k≠2.
(2)由(1)可知k≥-1,
∵k为最小整数,
∴k=-1,
∴方程②为,
∵方程②有两根分别为和,
∴+()=,即-m=-4,
解得:m=4.
(3)①根据题意补全图形如下,过点E作EP⊥x轴于P,过G作GQ⊥y轴于Q,由(2)可知k=-1,m=4,
∴直线AB解析式为y=-x+1,双曲线的解析式为,
∵直线y=kx+1与x轴,y轴分别交于点A,B,
∴A(1,0),B(0,1),
∴OA=OB=1,∠OBA=∠OAB=45°,
∴△AOB是等腰直角三角形,
∵EP⊥x轴,GQ⊥y轴,
∴△BQG和△EPA是等腰直角三角形,
∴BG=GQ,AE=PE,
∵CD⊥y轴,CF⊥x轴,
∴GQ=CD,PE=CF,
设点C坐标为(t,),则CD=t,CF=,
∴BG·AE=t×·=1.
②如图,连接OE、OG,
由①得BG·AE=1,OA=OB=1,∠OBA=∠OAB=45°,
∴BG=,
∴,
∴△BOG∽△AEO,
∴∠OGB=∠EOA,
∵∠OGB=∠GOA+∠OAB,∠EOA=∠EOG+∠GOA,
∴∠EOG=∠OAB=45°.
21.
(1)证明:,
,
为边上的高,
,
,
,
是的平分线,
,
.
(2)解:如图,作于.
∵∠BFD+∠ABE=90°,∠CEB+∠CBE=90°,∠ABE=∠CBE,
∴∠BFD=∠CEB,
∵∠BFD=∠CFE,
,
为等腰三角形,
,
,
∴点为的中点,
,
,
,
,
,
,
,,
,
,
根据,即,
,
,
,
,
.
22.
解:(1)函数的“特征数”是,,,函数的“特征数”是,2,,函数的“特征数”是,,,
“特征数”是,,的函数解析式是:,
函数的图象向下平移2个单位,
;
(2) “特征数”是的函数图象与、轴分别交点、,
函数解析式为:,
图象与、轴分别点、,
“特征数”是的函数图象与轴交于点,
函数解析式为:
图象与、轴分别点、,
,,.
,
又∠DOE=∠COD,
.
23.
解:(1)∵四边形OABC是矩形,点B坐标为(4,﹣3).
∴∠AOC=90°.OA=3,OC=4,
∴AC==5.
故答案为5;
(2)由折叠可得:DE⊥AC,AF=FC=,
∵∠FCD=∠OCA,∠DFC=∠AOC=90°,
∴△DFC∽△AOC.
∴==,
∴==,
∴DF=,DC=,
∴OD=OC﹣DC=4﹣=.
∴D(,0);
∵四边形OABC是矩形,
∴AB∥DC,
∴∠EAF=∠DCF,
在△AFE和△CFD中,,
∴△AFE≌△CFD(ASA).
∴EF=DF.
∴DE=2DF=2×=.
即折痕DE的长为.
(3)如图所示:
由(2)可知,AE=CD=
∴E(,﹣3),D(,0),
①当DE为菱形的边时,DP=DE=,可得Q(,﹣3),Q1(﹣,﹣3).
②当DE为菱形的对角线时,P与C重合,Q与A重合,Q2(0,﹣3),
③当点Q在第一象限,E与Q关于x轴对称,Q(,3)
综上所述,满足条件的点Q坐标为(,﹣3)或(﹣,﹣3)或(0,﹣3)或(,3).
24.
解:(1)∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠DCA=30°,
∴∠BCD=45°-30°=15°,
又∵BD⊥CD,
∴∠CBD=90°-15°=75°,
∴∠ABD=75°-45°=30°,
在Rt△ACE和Rt△BDE中,∠ACE=30°,∠ABD=30°,
∴ , ,
在△CEB和△AED中,
∠CEB=∠AED,,
∴△CEB∽△AED,
∴∠BAD=∠BCD=15°.
(2)如图,作三角形BCD的外接圆,则∠BCD为圆周角,
∵∠BDC=45°,
∴所对的圆心角为90°,
∵∠BAC=90°,
∴点A即为△BCD的外接圆的圆心,
∴AC=AD,
∵点F是CD中点,
∴AF⊥CD.
(3)如图,过点D作DE⊥BC于点E,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠BDA=3∠CBD,∠BDA=∠C+∠CBD,
∴∠C=2∠CBD,
∵∠ABC=∠ACB,∠ABC=∠ABD+∠CBD,
∴∠ABD=∠CBD,
又∵∠BAC=90°,DE⊥BC,
∴DE=AD,
设DE=AD=a,
易得△CED为等腰直角三角形,
∴CD=,
∴AB=AC=,
∵BD=,
∴在Rt△ABD中,,
解得 ,
∴AB=AC=,
∴BC=,
∴ .
25.
(1)∵AF∥BC,∴∠AFE=∠DBE.在△AEF和△DEB中,∵,∴△AEF≌△DEB;
(2)四边形ADCF是菱形,理由如下:
∵△AEF≌△DEB,∴AF=BD.
∵BD=DC,∴AF=DC.
又∵AF∥BC,∴四边形ADCF是平行四边形.
∵∠BAC=90°,AD是BC边上的中线,∴AD=DC,∴四边形ADCF是菱形;
(3)连接BF交AC于M,则点M即为所求.
∵四边形ADCF是菱形,∴点D与点F关于直线AC对称,∴MD=MF,∴MB+MD=MB+MF=BF,即MB+MD有最小值.
∵AF=DC=BD,∴BC=2AF.
∵AF∥BC,∴△AMF∽△CMB,∴,∴,∴AM=AC.
∵AC=2,∴AM=.
26.
(1)解:∵直线分别与轴和轴交于点B和点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
把,分别代入,
得,
解得,
∴抛物线的解析式为.
(2)∵抛物线与x轴交于点A,
∴,
解得,,
∴点A的坐标为,
∴,,
在中,,,
∴,
∴,
∵,
∴,
又∵,
∴.
(3)设点D的坐标为
则点E的坐标为
∴
=
∵,
∴当时,线段DE的长度最大.
此时,点D的坐标为,
∵,
∴点C和点M关于对称轴对称,
连接CD交对称轴于点P,此时最小.
连接CM交直线DE于点F,则,点F的坐标为,
∴,
∵
∴的最小值.
.
同课章节目录
