浙教版九年级数学上册4.4两个相似三角形的判定 同步测试(含答案)
文档属性
| 名称 | 浙教版九年级数学上册4.4两个相似三角形的判定 同步测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 655.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 10:40:21 | ||
图片预览




文档简介
4.4两个相似三角形的判定
一、单选题
1.如图,在中,点分别在的边上,如果添加下列其中之一的条件,不一定能使与相似,那么这个条件是( )
A. B.
C. D.
2.如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
3.如图正方形网格上的三角形(1)(2)(3)中与△ABC相似的是( )
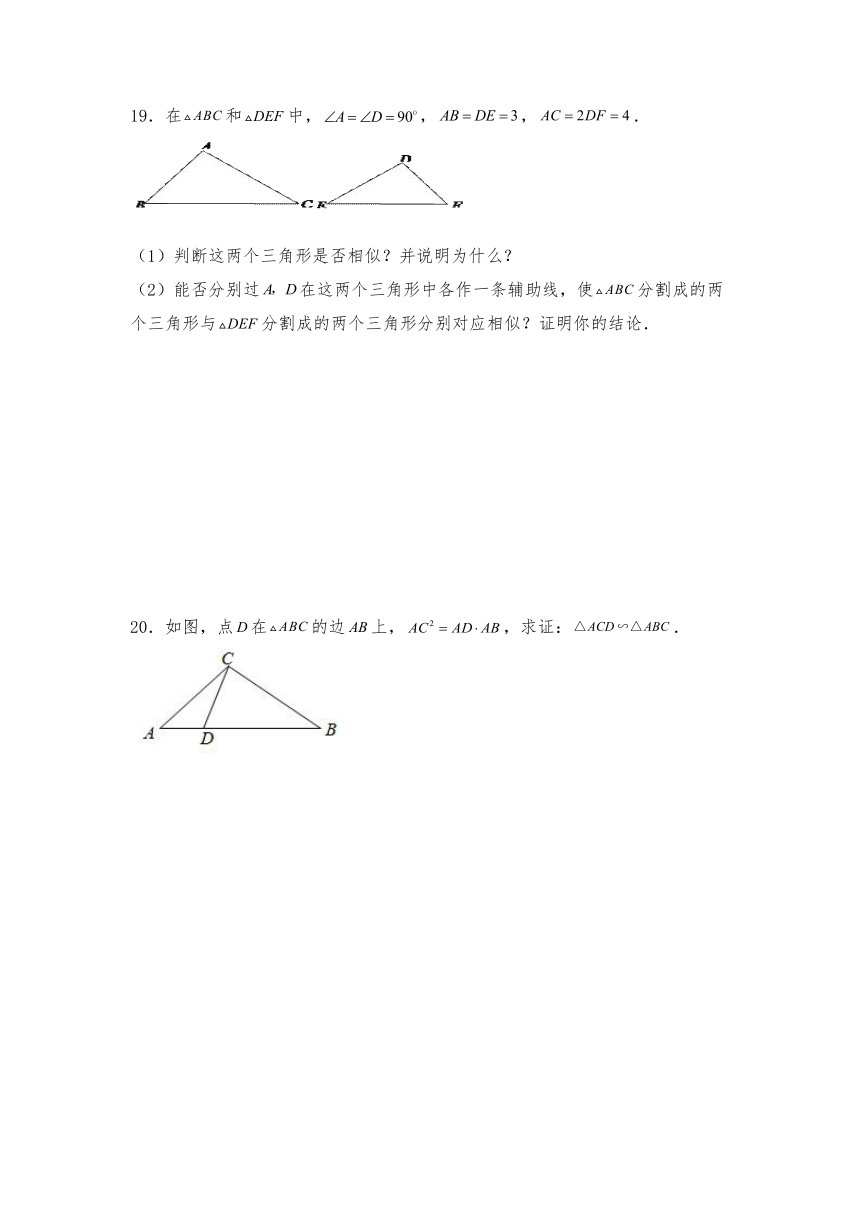
A.(1) B.(2)
C.(3) D.都不与△ABC相似
4.下列数据分别表示两个三角形的边,则两个三角形相似的是( )
A.3,2,4与9,12.6 B.2,4,5与4,9,12
C.3,4,5与2,2.5,1 D.2.5,5,4与0.5,1.1,1.5
5.下列命题中正确的是( ).
A.所有等腰三角形都相似 B.两边成比例的两个等腰三角形相似
C.有一个角相等的两个等腰三角形相似 D.有一个角是100°的两个等腰三角形相似
6.如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△ABC∽△ADE的是( )
A.∠ADE=∠B B.∠AED=∠C C. D.
7.下列说法正确的是()
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.有一角为65°的两个等腰三角形相似.
C.顺次连接一个四边形各边中点所得到的四边形是矩形,那么原四边形一定是菱形.
D.对角线互相垂直平分的四边形是菱形.
8.在△ABC中,∠B=∠C=36°,AD、AE三等分∠A,D、E在BC边上,则其中的相似三角形(不包含全等)有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
9.如图,⊙O是△ABC的外接圆,D是AC的中点,连结AD,BD,其中BD与AC交于点E.写出图中所有与△ADE相似的三角形:___________.
10.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是__.
11.如图,在中,,是上一点且,当________时,使得与相似.
12.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕,且,那么该矩形的周长为______cm.
13.平行四边形中,是中点,是中点,与交于,则______.
14.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为_____.
15.如图,在△ABC中,P,Q分别为AB,AC的中点.若S△APQ=1,则S四边形PBCQ=__.
16.如图,在正方形中,,将正方形的边沿折叠到,连接、、,若的面积为,则的面积为_______.
三、解答题
17.如图所示,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F.
(1)求证:△BEF∽△CDF;
(2)求证:DE·BF=EF·BC.
18.如图,在中,为边上一点,用尺规在边上求作一点E,使.(保留作图痕迹,不写作法)
19.在和中,,,.
(1)判断这两个三角形是否相似?并说明为什么?
(2)能否分别过在这两个三角形中各作一条辅助线,使分割成的两个三角形与分割成的两个三角形分别对应相似?证明你的结论.
20.如图,点在的边上,,求证:.
21.(1)如图1,在中,,,,请在图1中作一条直线,使得被分成两个等腰三角形,并在图中标注出相应的角度.
(2)如图2,在两个不相似的和中,,,,直线和直线将和分别分为两个三角形,并使的两部分能分别与的两部分相似.请在图中作出直线和直线,并标注出相应的角度.
22.如图①,在矩形ABCD中,AB=4,BC=m(m>1),点E、F分别在边AD、AB上,且AE=1.
(1)当m=3,AF:FB=1:3时,求证:AEF∽BFC;
(2)当m=3.5时,用直尺和圆规在图②的线段AB上确定所有使AEF与以点B、F、C为项点的三角形相似的点F(请保留画图痕迹);
(3)探究:对于每一个确定的m的值,线段AB上存在几个点F,使得AEF与以点B、F、C为顶点的三角形相似?(直接写出结论即可)
23.如图,已知矩形.
(1)在线段上作点,使得(要求:只需作出满足条件的一个点即可,尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,求证:.
24.已知:如图,BC为半圆的直径,O为圆心,D是弧AD的中点,四边形ABCD的对角线AC、BD交于点E.求证:△ABE∽△DBC.
25.如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
(1)求证:△AMN是等腰三角形;
(2)求BM AN的最大值;
(3)当M为BC中点时,求ME的长.
26.如图,线段A′B′是线段AB绕点O逆时针旋转后得到的图形(旋转角小于180°).
(1)用直尺和圆规作点O(保留作图痕迹,不写作法);
(2)连接OA、OA′、AA′、OB、OB′、BB′,求证:△OAA′∽△OBB′.
答案
一、单选题
D.D.B.AD.D.D.D.
二、填空题
9.△CBE,△BDA.
10.①②.
11..
12.72.
13.4:1
14..
15.3.
16.4.
三、解答题
17.
证明:证明:(1),,
,且,
;
(2)如图,连接,
,
点,点,点,点四点共圆,
,,
,
,
18.
如图,分以下四步:
(1)以点B为圆心,小于AD长为半径画弧,分别交AB、BC于点G、F
(2)以点D为圆心,BG长为半径画弧,交AD于点M
(3)以点M为圆心,GF长为半径画弧,与(2)所画的弧交内于点N
(4)连接DN,并延长DN,交AC于点E
则点E即为所作
理由如下:
由作图过程可知:,
在和中,
.
19.
(1)不相似.
在中,,;
在中,,,
.
.
与不相似.
(2)能作如图所示的辅助线进行分割.
具体作法:作,交于;作,交于.
由作法和已知条件可知.
,,
,,
.
,
,
..
20.
证明:∵,
∴.
又∵,
∴.
21.
解:(1)如图,直线AE即为所求作.
(2)如图,直线a,直线b即为所求作.
22.
(1)证明: ∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∵AE=1,BC=m=3,AF:FB=1:3,
∴,
∴AEF∽BFC;
解:(2)如图,延长DA,作点E关于AB的对称点E′,连接CE′,交AB于点F1;
连接CE,以CE为直径作圆交AB于点F2、F3.点F1、F2、F3即为所求;
(3)如(2)中所作图形,当m=4时,由已知条件可得DE=3,则CE=5,即圆的直径为5,由梯形中位线定理可得此时圆心到AB的距离为2.5,等于半径,点F2、F3重合,符合条件的点F有2个;当m>4时,圆和AB相离,此时点F2、F3不存在,即符合条件的点F只有1个;当1<m<4且m≠3时,符合条件的点F有3个;
综上所述,可得:当1<m<4且m≠3时,有3个;当m=3时,有2个;当m=4时,有2个;当m>4时,有1个.
23.
(1)解:先作BC的垂直平分线HF,交BC与G,然后以点G为圆心,以BG长为半径作圆,交AD与E点,连结BE,CE,
∵BC为直径,点E在圆上,
∴∠BEC=90°,
如图,点E即为所求.
(2)证:∵四边形是矩形,
∴.
∴.
∵,
∴.
∴.
∴.
24.
解:∵BC为半圆的直径,
∴∠BAC=∠BDC=90°,
∵D是弧AD的中点,即,
∴∠ABD=∠CBD,
∵∠BAE=∠BDC,∠ABE=∠DBC,
∴△ABE∽△DBC.
25.(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠NAM=∠BMA,又∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
(2)如图,作NH⊥AM于H,
∵AN=MN,NH⊥AM,
∴AH=AM,
∵∠NHA=∠ABM=90°,∠AMN=∠AMB,
∴△NAH∽△AMB,
∴,
∴AN BM=AH AM=,
在Rt△AMB中,,
∵BM≤2,
∴9+≤13,
∴AN BM≤,
即当BM=2时,BM AN的最大值为;
(3)解:∵M为BC中点,
∴BM=CM=BC=1,
由(2)得,AN BM=,
∵==10,
∴AN=5,
∴DN=5﹣2=3,
设DE=x,则CE=3﹣x,
∵AN∥BC,
∴,即,
解得,x=,即CE=,
∴CE=,
∴ME==.
26.
解:(1)如图,点O即为所求.
(2)证明:如图,
∵线段A′B′为线段AB绕点O逆时针旋转后的图形,
∴OA=OA′,OB=OB′,∠AOA′=∠BOB′.
∴=.
∴△OAA′∽△OBB′.
一、单选题
1.如图,在中,点分别在的边上,如果添加下列其中之一的条件,不一定能使与相似,那么这个条件是( )
A. B.
C. D.
2.如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
3.如图正方形网格上的三角形(1)(2)(3)中与△ABC相似的是( )
A.(1) B.(2)
C.(3) D.都不与△ABC相似
4.下列数据分别表示两个三角形的边,则两个三角形相似的是( )
A.3,2,4与9,12.6 B.2,4,5与4,9,12
C.3,4,5与2,2.5,1 D.2.5,5,4与0.5,1.1,1.5
5.下列命题中正确的是( ).
A.所有等腰三角形都相似 B.两边成比例的两个等腰三角形相似
C.有一个角相等的两个等腰三角形相似 D.有一个角是100°的两个等腰三角形相似
6.如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△ABC∽△ADE的是( )
A.∠ADE=∠B B.∠AED=∠C C. D.
7.下列说法正确的是()
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.有一角为65°的两个等腰三角形相似.
C.顺次连接一个四边形各边中点所得到的四边形是矩形,那么原四边形一定是菱形.
D.对角线互相垂直平分的四边形是菱形.
8.在△ABC中,∠B=∠C=36°,AD、AE三等分∠A,D、E在BC边上,则其中的相似三角形(不包含全等)有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
9.如图,⊙O是△ABC的外接圆,D是AC的中点,连结AD,BD,其中BD与AC交于点E.写出图中所有与△ADE相似的三角形:___________.
10.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是__.
11.如图,在中,,是上一点且,当________时,使得与相似.
12.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕,且,那么该矩形的周长为______cm.
13.平行四边形中,是中点,是中点,与交于,则______.
14.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为_____.
15.如图,在△ABC中,P,Q分别为AB,AC的中点.若S△APQ=1,则S四边形PBCQ=__.
16.如图,在正方形中,,将正方形的边沿折叠到,连接、、,若的面积为,则的面积为_______.
三、解答题
17.如图所示,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F.
(1)求证:△BEF∽△CDF;
(2)求证:DE·BF=EF·BC.
18.如图,在中,为边上一点,用尺规在边上求作一点E,使.(保留作图痕迹,不写作法)
19.在和中,,,.
(1)判断这两个三角形是否相似?并说明为什么?
(2)能否分别过在这两个三角形中各作一条辅助线,使分割成的两个三角形与分割成的两个三角形分别对应相似?证明你的结论.
20.如图,点在的边上,,求证:.
21.(1)如图1,在中,,,,请在图1中作一条直线,使得被分成两个等腰三角形,并在图中标注出相应的角度.
(2)如图2,在两个不相似的和中,,,,直线和直线将和分别分为两个三角形,并使的两部分能分别与的两部分相似.请在图中作出直线和直线,并标注出相应的角度.
22.如图①,在矩形ABCD中,AB=4,BC=m(m>1),点E、F分别在边AD、AB上,且AE=1.
(1)当m=3,AF:FB=1:3时,求证:AEF∽BFC;
(2)当m=3.5时,用直尺和圆规在图②的线段AB上确定所有使AEF与以点B、F、C为项点的三角形相似的点F(请保留画图痕迹);
(3)探究:对于每一个确定的m的值,线段AB上存在几个点F,使得AEF与以点B、F、C为顶点的三角形相似?(直接写出结论即可)
23.如图,已知矩形.
(1)在线段上作点,使得(要求:只需作出满足条件的一个点即可,尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,求证:.
24.已知:如图,BC为半圆的直径,O为圆心,D是弧AD的中点,四边形ABCD的对角线AC、BD交于点E.求证:△ABE∽△DBC.
25.如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
(1)求证:△AMN是等腰三角形;
(2)求BM AN的最大值;
(3)当M为BC中点时,求ME的长.
26.如图,线段A′B′是线段AB绕点O逆时针旋转后得到的图形(旋转角小于180°).
(1)用直尺和圆规作点O(保留作图痕迹,不写作法);
(2)连接OA、OA′、AA′、OB、OB′、BB′,求证:△OAA′∽△OBB′.
答案
一、单选题
D.D.B.AD.D.D.D.
二、填空题
9.△CBE,△BDA.
10.①②.
11..
12.72.
13.4:1
14..
15.3.
16.4.
三、解答题
17.
证明:证明:(1),,
,且,
;
(2)如图,连接,
,
点,点,点,点四点共圆,
,,
,
,
18.
如图,分以下四步:
(1)以点B为圆心,小于AD长为半径画弧,分别交AB、BC于点G、F
(2)以点D为圆心,BG长为半径画弧,交AD于点M
(3)以点M为圆心,GF长为半径画弧,与(2)所画的弧交内于点N
(4)连接DN,并延长DN,交AC于点E
则点E即为所作
理由如下:
由作图过程可知:,
在和中,
.
19.
(1)不相似.
在中,,;
在中,,,
.
.
与不相似.
(2)能作如图所示的辅助线进行分割.
具体作法:作,交于;作,交于.
由作法和已知条件可知.
,,
,,
.
,
,
..
20.
证明:∵,
∴.
又∵,
∴.
21.
解:(1)如图,直线AE即为所求作.
(2)如图,直线a,直线b即为所求作.
22.
(1)证明: ∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∵AE=1,BC=m=3,AF:FB=1:3,
∴,
∴AEF∽BFC;
解:(2)如图,延长DA,作点E关于AB的对称点E′,连接CE′,交AB于点F1;
连接CE,以CE为直径作圆交AB于点F2、F3.点F1、F2、F3即为所求;
(3)如(2)中所作图形,当m=4时,由已知条件可得DE=3,则CE=5,即圆的直径为5,由梯形中位线定理可得此时圆心到AB的距离为2.5,等于半径,点F2、F3重合,符合条件的点F有2个;当m>4时,圆和AB相离,此时点F2、F3不存在,即符合条件的点F只有1个;当1<m<4且m≠3时,符合条件的点F有3个;
综上所述,可得:当1<m<4且m≠3时,有3个;当m=3时,有2个;当m=4时,有2个;当m>4时,有1个.
23.
(1)解:先作BC的垂直平分线HF,交BC与G,然后以点G为圆心,以BG长为半径作圆,交AD与E点,连结BE,CE,
∵BC为直径,点E在圆上,
∴∠BEC=90°,
如图,点E即为所求.
(2)证:∵四边形是矩形,
∴.
∴.
∵,
∴.
∴.
∴.
24.
解:∵BC为半圆的直径,
∴∠BAC=∠BDC=90°,
∵D是弧AD的中点,即,
∴∠ABD=∠CBD,
∵∠BAE=∠BDC,∠ABE=∠DBC,
∴△ABE∽△DBC.
25.(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠NAM=∠BMA,又∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
(2)如图,作NH⊥AM于H,
∵AN=MN,NH⊥AM,
∴AH=AM,
∵∠NHA=∠ABM=90°,∠AMN=∠AMB,
∴△NAH∽△AMB,
∴,
∴AN BM=AH AM=,
在Rt△AMB中,,
∵BM≤2,
∴9+≤13,
∴AN BM≤,
即当BM=2时,BM AN的最大值为;
(3)解:∵M为BC中点,
∴BM=CM=BC=1,
由(2)得,AN BM=,
∵==10,
∴AN=5,
∴DN=5﹣2=3,
设DE=x,则CE=3﹣x,
∵AN∥BC,
∴,即,
解得,x=,即CE=,
∴CE=,
∴ME==.
26.
解:(1)如图,点O即为所求.
(2)证明:如图,
∵线段A′B′为线段AB绕点O逆时针旋转后的图形,
∴OA=OA′,OB=OB′,∠AOA′=∠BOB′.
∴=.
∴△OAA′∽△OBB′.
同课章节目录
