九年级数学上册试题 4.5相似三角形的性质及其应用同步测试-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.5相似三角形的性质及其应用同步测试-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 00:00:00 | ||
图片预览




文档简介
4.5相似三角形的性质及其应用
一、单选题
1.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
2.如图,在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上,AD∥EF,如果AE:AB=1:3,AD=4,BC=10,那么EF的长为( )
A.5 B.6 C.7 D.8
3.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B、D的对应点为A、C,那么需要添加的一个条件是( )
A.CE= B.CE= C.AC=BD D.AC∥BD
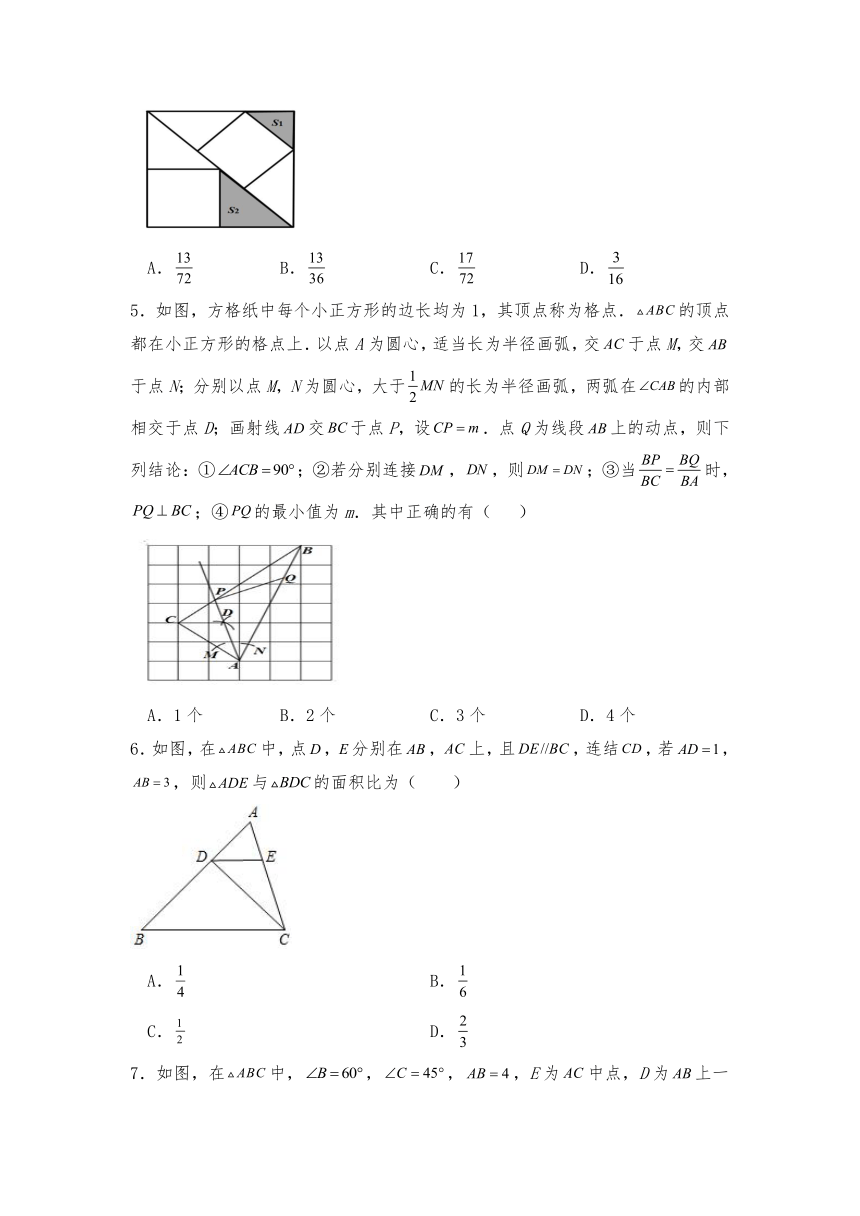
4.有3个正方形按如图所示放置,其中大正方形的边长是1,阴影部分的面积依次记为S1,S2,则S1+S2等于( )
A. B. C. D.
5.如图,方格纸中每个小正方形的边长均为1,其顶点称为格点.的顶点都在小正方形的格点上.以点A为圆心,适当长为半径画弧,交于点M,交于点N;分别以点M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点D;画射线交于点P,设.点Q为线段上的动点,则下列结论:①;②若分别连接,,则;③当时,;④的最小值为m.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在中,点,分别在,上,且,连结,若,,则与的面积比为( )
A. B.
C. D.
7.如图,在中,,,,E为中点,D为上一点,连接,当时,的长为( )
A. B. C.3 D.
8.如图,在菱形中,点,分别在,上,且,点,分别是的三等分点,则的值为( )
A. B. C. D.
二、填空题
9.如图,在ABC中,点D是边AC上的任意一点,点M,N分别是ABD和BCD的重心,如果AC=6,那么线段MN的长为 ___.
10.如图,P为平行四边形ABCD边BC上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为S、S1、S2.若S=2,则S1+S2=_____.
11.如图,在ABC中,AB=6,BC=12,点P是AB边的中点,点Q是BC边上一个动点,当BQ=___________时,BPQ与BAC相似.
12.如图,一张矩形纸片ABCD,点E在AB边上,把沿直线CE,使点B落在对角线AC上的点F处,联结DF,若点E、F、D在同一直线上,.则______.
13.如图,平行四边形ABCD中,AB:BC=3:2,∠BAD和∠ABC的平分线交CD于E、F两点,AE、BF交于点G,则△EFG和△ABG面积的比值是_______________.
14.如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O.若S△EOB=1,则四边形AECD的面积为 ___.
15.如图,△ABC中,BC=6,点D,E分别在边AB,AC上,DE∥BC,且S△ADE=SDBCE,则DE=___.
16.有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则的长_______________________.
三、解答题
17.数学小组想利用所学知识测量一棵树的高度.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树梢影子末端重合于点H,测得米.随后,组员在直线上平放一平面镜,在镜面上做了一个标记,这个标记在直线上的对应位置为点G.镜子不动,小莉从点D沿着直线后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时米.如图,已知,,,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度.
18.在中,,是中线,,,、分别在、的延长线上,与交于点,与交于点.
(1)如图1,若,求证:;
(2)如图2,求证;
(3)若,,求的长.
19.如图,在和中,,,求的度数.
20.如图,小亮同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶B在同一直线上.已知纸板的两条边EF=30cm,DE=40cm,延长DF交AB于点C,测得边DF离地面的高度AC=1.5m,CD=12m,求树高AB.
21.如图,在ABC中,AB=AC=6,BC=5,D是AB上一点,BD=2,E是BC上一动点,连接DE,作∠DEF=∠B,射线EF交线段AC于F.
(1)求证:DBE∽ECF;
(2)当F是线段AC中点时,求线段BE的长.
22.如图,在矩形ABCD中,E,F分别是AB,AD的中点,连接AC,EC,EF,FC,且EC⊥EF.
(1)求证:△AEF∽△BCE;
(2)若AC=,求AB的长.
23.如图,在中,,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出吗?
24.如图,在中,,是的高,连接.
(1)求证:;
(2)若,,求的长.
25.如图所示,点P是 ABCD的边DC的延长线上一点,连结AP分别交BD、BC于点M、N.
求证:AM2=MN MP.
26.如图①,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)(证明与推断):①求证:四边形CEGF是正方形;
②的值为 ;
(2)(探究与证明):将正方形CEGF绕点C顺时针方向旋转α度(0°<α<45°),如图②所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)(拓展与运用):正方形CEGF在旋转过程中,当A,G,F三点在同一直线上时,如图③所示,延长CG交AD于点H.
①求证:△ACH∽△GAH;
②若AG=6,GH=2,求BC的长.
答案
一、单选题
C.B.B.A.D.B.C.D.
二、填空题
9.2
10.18
11.1.5或6.
12.
13..
14.9.
15..
16..
三、解答题
17.
设 ,,
,,,,
,,
,
又,
即
.
答:树的高度为米.
18.
(1)证明:∵∠ACB=90°,AC=BC,CD是中线,
∴∠ACD=∠BCD=45°,∠ACF=∠BCE=90°,
∴∠DCF=∠DCE=135°,
在△DCF和△DCE中,
,
∴△DCF≌△DCE(SAS)
∴DE=DF;
(2)证明:∵∠DCF=135°,
∴∠F+∠CDF=45°,
∵∠FDE=45°,
∴∠CDE+∠CDF=45°,
∴∠F=∠CDE,
∵∠DCF=∠DCE,∠F=∠CDE,
∴△FCD∽△DCE,
∴,
∴CD2=CE CF;
(3)解:过点D作DG⊥BC于G,
∵∠DCB=45°,
∴GC=GD=CD=,
由(2)可知,CD2=CE CF,
∴CE==2,
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△ENC∽△DNG,
∴,即,
解得,NG=,
由勾股定理得,DN=.
19.
解:在和中,,
,
,
,
.
20.
解:∠DEF=∠DCB = 90°,∠EDF=∠CDB,
△DEF△DCB,
在Rt△DEF中,
答:树高AB是10.5m.
21.
(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠B=∠DEF,
∴∠DEF=∠C,
又∵∠BEF=∠BED+∠DEF=∠C+∠CFE,
∴∠BED=∠CFE,
∴DBE∽ECF;
(2)解:∵F是线段AC中点,AC=6,
∴AF=FC=3,
∵DBE∽ECF,
∴,
设BE=x,则EC=5﹣x,
∴,
解得:x=3或x=2,
经检验x=3和x=2都是原方程的根,
∴BE的长为2或3.
22.
(1)证明:∵四边形ABCD是矩形,
∴∠EAF=∠CBE=90°,
∴∠AEF+∠AFE=90°,
∵EC⊥EF,
∴∠FEC=90°,
∴∠AEF+∠BEC=90°,
∴∠AFE=∠BEC,
∵∠EAF=∠CBE=90°,
∴△AEF∽△BCE;
(2)解:∵四边形ABCD是矩形,
∴AD=BC,
∵E、F分别是AB、AD的中点
∴AE=BE=AD,
设AE=x,AF=y,
则BE=x,AB=2x,BC=AD=2y,
∵△AEF∽BCE,
∴,
∴,
∴x2=2y2,
∵∠B=90°,
∴AB2+BC2=AC2,
∴(2x)2+(2y)2=(2)2,
∴x2+y2=3,
∴2y2+y2=3,
解得y=1,,
∴AE=,AF=1,
∵点E是AB的中点,
∴AB=2AE=2.
23.
解:(1),,;
(2)能,
,
,
,
,
,
,
,
,
;
24.
(1)证明:∵BD,CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ABD∽△ACE.
,
,
∵,
;
(2)∵
,
,则,
,
又,
,
.
25.
证明:∵在 ABCD中,,
,,
,
,
∵在 ABCD中,,
,,
,
,
,
;
26.
解:(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴,GE∥AB,
∴,
故答案为:;
(2)连接CG,
由旋转性质知∠BCE=∠ACG=α,
△CEG和△CBA都是等腰直角三角形,
∴CG=CE,CA=CB,
∴,
∴△ACG∽△BCE,
∴,
∴线段AG与BE之间的数量关系为AG=BE;
(3)①由(2)知△BCE∽△ACG,
∴∠AGC=∠BEC=135°,
∵∠CGF=45°,
∴∠AGC+∠CGF=180°,
∴A、G、F三点共线.
∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△ACH∽△GAH;
②由①知,△ACH∽△GAH,则,
设BC=CD=AD=a,则AC=a,
∵,
∴,
∴AH=a,
则DH=AD-AH=a,CH==a,
由得,
解得:a=3,即BC=3.
一、单选题
1.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
2.如图,在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上,AD∥EF,如果AE:AB=1:3,AD=4,BC=10,那么EF的长为( )
A.5 B.6 C.7 D.8
3.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B、D的对应点为A、C,那么需要添加的一个条件是( )
A.CE= B.CE= C.AC=BD D.AC∥BD
4.有3个正方形按如图所示放置,其中大正方形的边长是1,阴影部分的面积依次记为S1,S2,则S1+S2等于( )
A. B. C. D.
5.如图,方格纸中每个小正方形的边长均为1,其顶点称为格点.的顶点都在小正方形的格点上.以点A为圆心,适当长为半径画弧,交于点M,交于点N;分别以点M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点D;画射线交于点P,设.点Q为线段上的动点,则下列结论:①;②若分别连接,,则;③当时,;④的最小值为m.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在中,点,分别在,上,且,连结,若,,则与的面积比为( )
A. B.
C. D.
7.如图,在中,,,,E为中点,D为上一点,连接,当时,的长为( )
A. B. C.3 D.
8.如图,在菱形中,点,分别在,上,且,点,分别是的三等分点,则的值为( )
A. B. C. D.
二、填空题
9.如图,在ABC中,点D是边AC上的任意一点,点M,N分别是ABD和BCD的重心,如果AC=6,那么线段MN的长为 ___.
10.如图,P为平行四边形ABCD边BC上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为S、S1、S2.若S=2,则S1+S2=_____.
11.如图,在ABC中,AB=6,BC=12,点P是AB边的中点,点Q是BC边上一个动点,当BQ=___________时,BPQ与BAC相似.
12.如图,一张矩形纸片ABCD,点E在AB边上,把沿直线CE,使点B落在对角线AC上的点F处,联结DF,若点E、F、D在同一直线上,.则______.
13.如图,平行四边形ABCD中,AB:BC=3:2,∠BAD和∠ABC的平分线交CD于E、F两点,AE、BF交于点G,则△EFG和△ABG面积的比值是_______________.
14.如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O.若S△EOB=1,则四边形AECD的面积为 ___.
15.如图,△ABC中,BC=6,点D,E分别在边AB,AC上,DE∥BC,且S△ADE=SDBCE,则DE=___.
16.有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则的长_______________________.
三、解答题
17.数学小组想利用所学知识测量一棵树的高度.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树梢影子末端重合于点H,测得米.随后,组员在直线上平放一平面镜,在镜面上做了一个标记,这个标记在直线上的对应位置为点G.镜子不动,小莉从点D沿着直线后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时米.如图,已知,,,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度.
18.在中,,是中线,,,、分别在、的延长线上,与交于点,与交于点.
(1)如图1,若,求证:;
(2)如图2,求证;
(3)若,,求的长.
19.如图,在和中,,,求的度数.
20.如图,小亮同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶B在同一直线上.已知纸板的两条边EF=30cm,DE=40cm,延长DF交AB于点C,测得边DF离地面的高度AC=1.5m,CD=12m,求树高AB.
21.如图,在ABC中,AB=AC=6,BC=5,D是AB上一点,BD=2,E是BC上一动点,连接DE,作∠DEF=∠B,射线EF交线段AC于F.
(1)求证:DBE∽ECF;
(2)当F是线段AC中点时,求线段BE的长.
22.如图,在矩形ABCD中,E,F分别是AB,AD的中点,连接AC,EC,EF,FC,且EC⊥EF.
(1)求证:△AEF∽△BCE;
(2)若AC=,求AB的长.
23.如图,在中,,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出吗?
24.如图,在中,,是的高,连接.
(1)求证:;
(2)若,,求的长.
25.如图所示,点P是 ABCD的边DC的延长线上一点,连结AP分别交BD、BC于点M、N.
求证:AM2=MN MP.
26.如图①,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)(证明与推断):①求证:四边形CEGF是正方形;
②的值为 ;
(2)(探究与证明):将正方形CEGF绕点C顺时针方向旋转α度(0°<α<45°),如图②所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)(拓展与运用):正方形CEGF在旋转过程中,当A,G,F三点在同一直线上时,如图③所示,延长CG交AD于点H.
①求证:△ACH∽△GAH;
②若AG=6,GH=2,求BC的长.
答案
一、单选题
C.B.B.A.D.B.C.D.
二、填空题
9.2
10.18
11.1.5或6.
12.
13..
14.9.
15..
16..
三、解答题
17.
设 ,,
,,,,
,,
,
又,
即
.
答:树的高度为米.
18.
(1)证明:∵∠ACB=90°,AC=BC,CD是中线,
∴∠ACD=∠BCD=45°,∠ACF=∠BCE=90°,
∴∠DCF=∠DCE=135°,
在△DCF和△DCE中,
,
∴△DCF≌△DCE(SAS)
∴DE=DF;
(2)证明:∵∠DCF=135°,
∴∠F+∠CDF=45°,
∵∠FDE=45°,
∴∠CDE+∠CDF=45°,
∴∠F=∠CDE,
∵∠DCF=∠DCE,∠F=∠CDE,
∴△FCD∽△DCE,
∴,
∴CD2=CE CF;
(3)解:过点D作DG⊥BC于G,
∵∠DCB=45°,
∴GC=GD=CD=,
由(2)可知,CD2=CE CF,
∴CE==2,
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△ENC∽△DNG,
∴,即,
解得,NG=,
由勾股定理得,DN=.
19.
解:在和中,,
,
,
,
.
20.
解:∠DEF=∠DCB = 90°,∠EDF=∠CDB,
△DEF△DCB,
在Rt△DEF中,
答:树高AB是10.5m.
21.
(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠B=∠DEF,
∴∠DEF=∠C,
又∵∠BEF=∠BED+∠DEF=∠C+∠CFE,
∴∠BED=∠CFE,
∴DBE∽ECF;
(2)解:∵F是线段AC中点,AC=6,
∴AF=FC=3,
∵DBE∽ECF,
∴,
设BE=x,则EC=5﹣x,
∴,
解得:x=3或x=2,
经检验x=3和x=2都是原方程的根,
∴BE的长为2或3.
22.
(1)证明:∵四边形ABCD是矩形,
∴∠EAF=∠CBE=90°,
∴∠AEF+∠AFE=90°,
∵EC⊥EF,
∴∠FEC=90°,
∴∠AEF+∠BEC=90°,
∴∠AFE=∠BEC,
∵∠EAF=∠CBE=90°,
∴△AEF∽△BCE;
(2)解:∵四边形ABCD是矩形,
∴AD=BC,
∵E、F分别是AB、AD的中点
∴AE=BE=AD,
设AE=x,AF=y,
则BE=x,AB=2x,BC=AD=2y,
∵△AEF∽BCE,
∴,
∴,
∴x2=2y2,
∵∠B=90°,
∴AB2+BC2=AC2,
∴(2x)2+(2y)2=(2)2,
∴x2+y2=3,
∴2y2+y2=3,
解得y=1,,
∴AE=,AF=1,
∵点E是AB的中点,
∴AB=2AE=2.
23.
解:(1),,;
(2)能,
,
,
,
,
,
,
,
,
;
24.
(1)证明:∵BD,CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ABD∽△ACE.
,
,
∵,
;
(2)∵
,
,则,
,
又,
,
.
25.
证明:∵在 ABCD中,,
,,
,
,
∵在 ABCD中,,
,,
,
,
,
;
26.
解:(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴,GE∥AB,
∴,
故答案为:;
(2)连接CG,
由旋转性质知∠BCE=∠ACG=α,
△CEG和△CBA都是等腰直角三角形,
∴CG=CE,CA=CB,
∴,
∴△ACG∽△BCE,
∴,
∴线段AG与BE之间的数量关系为AG=BE;
(3)①由(2)知△BCE∽△ACG,
∴∠AGC=∠BEC=135°,
∵∠CGF=45°,
∴∠AGC+∠CGF=180°,
∴A、G、F三点共线.
∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△ACH∽△GAH;
②由①知,△ACH∽△GAH,则,
设BC=CD=AD=a,则AC=a,
∵,
∴,
∴AH=a,
则DH=AD-AH=a,CH==a,
由得,
解得:a=3,即BC=3.
同课章节目录
