浙教版九年级数学上册试题 4.5相似三角形的性质及其应用同步练习(含答案)
文档属性
| 名称 | 浙教版九年级数学上册试题 4.5相似三角形的性质及其应用同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 01:04:03 | ||
图片预览




文档简介
4.5相似三角形的性质及其应用
一、单选题
1.如图,在中,,,是边上一点,且,连接,把沿翻折,得到,与交于点,连接,则的面积为( )
A. B. C. D.
2.如图,边长为10的等边中,点D在边上,且,将含角的直角三角板()绕直角顶点D旋转,分别交边于P、Q,连接,当时,的长为( )
A.6 B. C. D.
3.如图,在平面直角坐标系中,菱形的对称中心恰好是原点O,已知点B坐标是,双曲线经过点A,则菱形的面积是( )
A. B.18 C. D.25
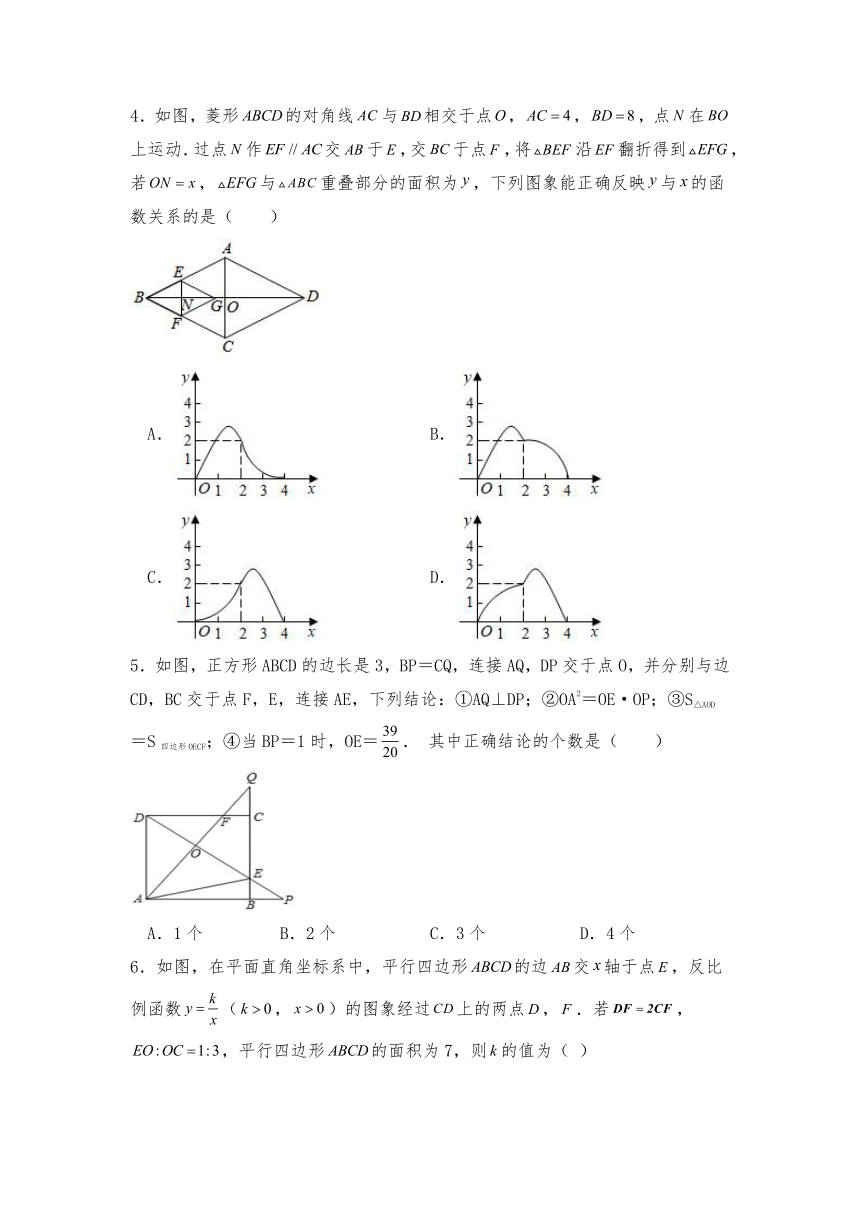
4.如图,菱形的对角线与相交于点,,,点在上运动.过点作交于,交于点,将沿翻折得到,若,与重叠部分的面积为,下列图象能正确反映与的函数关系的是( )
A. B.
C. D.
5.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE·OP;③S△AOD=S四边形OECF;④当BP=1时,OE=. 其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系中,平行四边形的边交轴于点,反比例函数(,)的图象经过上的两点,.若,,平行四边形的面积为7,则的值为( )
A. B. C.2 D.
7.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是( )
A. B. C.2- D.-1
8.如图,在正方形ABCD中,,M是AD边上的一点,.将沿BM对折至,连接DN,则DN的长是( )
A. B. C.3 D.
二、填空题
9.如图,边长为5的圆内接正方形ABCD中,P为CD的中点,连按AP并延长交圆于点E,则DE的长为___.
10.如图,在平面直角坐标系中,反比例函数的图象过点,连接,过点作的垂线交反比例函数图象于另一点,若,点的横坐标为,则的值是_____________.
11.如图,在三角形中,点D为边的中点,连接,将三角形沿直线翻折至三角形平面内,使得B点与E点重合,连接、,分别与边交于点H,与交于点O,若,,,则点A到线段的距离为__________.
12.在中学数学中求一些图形面积时,经常用到“同底等高”“等底等高”等数学思想方法,我们称它为等积变换.如图,BD为的对角线,M、N分别在AD、AB上,且,若,则__________.
13.如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,设BE=x,则CF=____(用x表示);则GM的最小值为_____.
14.如图,是小明家客厅地面铺设的瓷砖图案,其中四边形是正方形,阴影部分是四个全等的菱形,且点A、E、F在同一条直线上.已知菱形较短的对角线长为,则正方形的面积为_________.
15.已知:正方形ABCD中,E为BC的中点,BP=2AP,F为AD上一点,EF交CP于O,∠POF=45°,若APF的面积为,则线段EF的长为___.
16.如图,已知,,的中垂线交于点D、交于点M.下列结论:①是的平分线:②是等腰三角形;③;④.正确的有_______.
三、解答题
17.已知,如图,在矩形ABCD中,,,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度也为1cm/s:当一个点停止运动时,另一个点也停止运动:联结PO并延长,交BC于点E,过点Q作,交BD与点F,设运动时间为.
(1)当t为何值时,是等腰三角形;
(2)设五边形OECQF的面积为,求S关于t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使OD平分 若存在求出t的值;若不存在,请说明理由.
18.已知:如图,在矩形和等腰中,,,.点从点出发,沿方向匀速运动.速度为;同时,点从点出发,沿方向匀速运动,速度为.过点作,交于点,交于点,过点作,交于点.分别连接,,设运动时间为.
解答下列问题:
(1)当时,求的值;
(2)设五边形的面积为,求与之间的函数关系式;
(3)当时,求的值;
(4)若与相交于点,分别连接和.在运动过程中,是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
19.(阅读)定义:如果一个三角形一条边上的高与这条边的比值是4:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(理解)(1)如图1,在△ABC中,AC=8,BC=5,∠ACB=30°,试判断△ABC是否是“准黄金”三角形,请说明理由.
(应用)(2)如图2,△ABC是“准黄金”三角形,BC是“金底”,把△ABC沿BC翻折得到△DBC,AD交BC的延长线于点E,若点C恰好是△ABD的重心,求的值.
(拓展)(3)如图3,a∥b,且直线a与b之间的距离为4,“准黄金”△ABC的“金底”BC在直线b上,点A在直线a上,=,若∠ABC是钝角,将△ABC绕点C按顺时针方向旋转得到△A′B′C,线段A′C交a于点D.当点B′落在直线b上时,求的值.
20.(1)问题背景:如图1,正方形ABCD中,F在直线CD上,E在直线BC上.若∠EAF=45°,求证:BE+FD=EF;
(2)迁移应用:如图2,将正方形ABCD的一部分沿GH翻折,使A点的对应点E在BC上,且AD的对应边EM交CD于F点.若BE=3,EC=2,求EF的长;
(3)联系拓展:如图3,正方形ABCD中,E、Q在CD上,F在BC上,若EF=EA,∠FQA=∠FEA.若∠CFQ=34°,则∠QAD=_______°.
21.如图,矩形ABCD是⊙O的内接矩形,⊙O半径为5,AB=8,点E、F分别是弦CD、BC上的动点,连结EF,∠EAF始终保持等于45°.
(1)求AD的长度.
(2)已知DE=,求BF的长度.
(3)试探究△AEF的面积是否存在最小值,若存在,请求出它的最小值;若不存在,请说明理由.
22.如图,等腰三角形的腰长,,动点从出发沿向运动,速度为,动点从出发沿向运动,速度为,当一个点到达终点时两个点同时停止运动.点是点关于直线的对称点,连接和,和相交于点.设运动时间为秒.
(1)若当的值是多少时,恰好经过点
(2)设的面积为,求与之间的函数关系式.
(3)是否存在某一时刻,使平分 若存在,求出相应的值,若不存在,请说明理由.
(4)是否存在某一时刻,使点在的垂直平分线上 若存在,求出相应的值,若不存在,请说明理由.
23.如图,已知:在矩形ABCD中,AB=6cm,BC=8cm,点P从点B出发,沿BC方向匀速运动,速度为2cm/s;与点P同时,点Q从D点出发,沿DA方向匀速运动,速度为1cm/s;过点Q作QE//AC,交DC于点E. 设运动时间为t (s),(0<t<4),解答下列问题:
(1)在运动过程中,是否存在某一时刻t,使点P在AC的垂直平分线上?若存在,求出t的值;若不存在,请说明理由;
(2)设五边形APCEQ的面积为y,求y与t的函数关系式:
(3)当0<t<时,是否存在某一时刻t,使△PQE是直角三角形?若存在,求出t的值;若不存在,请说明理由.
24.抛物线y=ax2+b经过点A(4,0),B(0,﹣4),直线EC过点E(4,﹣1),C(0,﹣3),点P是抛物线上点A、B间的动点(不含端点A、B),过P作PD⊥x轴于点D,连接PC、PE.
(1)求抛物线与直线CE的解析式;
(2)求证:PC+PD为定值;
(3)若△PEC的面积为1,求满足条件的点P的坐标.
25.
如图,在△ABC中,点D、E分别是AB与AC的中点,可以猜想:DE∥BC且DE=BC.请用演绎推理给出证明.
(1)如图①,在矩形ABCD中,点M、N、P、Q分别为AB、BC、CD、DA的中点,顺次连结M、N、P、Q.求证:四边形MNPQ是菱形.
(2)如图②,在△ABC中,F是BC边中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=60°,则FE的长为 .
26.如图,平行四边形ABCD的对角线AC、BD交于点O,点E为边BC上一点,连接AE交BD于点F.
(1)求证:BE AF=BC EF;
(2)若AC⊥AB,AE⊥BC,BE=3,AB=4,求的值.
答案
一、单选题
B.B.C.A.C.A.A.D.
二、填空题
9.
10.
11.
12.7
13.,.
14.
15.
16.①②③.
三、解答题
17.
解:(1)∵在矩形ABCD中,AB=6cm,BC=8cm,∠ABC=90°,
∴AC=10,,点O到AD的距离为3,
当为等腰三角形时,分三种情况讨论:
当AP=PO=t时
过P作PM⊥AO,如图1所示:
∴,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ACD,
∴
∴,
∴;
②当;
③当时即点P与点D重合,.不合题意,舍去.
综上所述,当或5s时,为等腰三角形
(2)在矩形ABCD中,,,
∴
∵,
∴,
∴,
在矩形ABCD中,AD//BC, AO=CO,又得∠AOP=∠COE,
∴∠PAO=∠ECO,
∴△AOP≌COE,
∴AP=EC=t,
∴,
∴
(3)存在,理由如下:
如图3,过D作DM⊥PE于M,DN⊥AC于N,
在矩形ABCD中,,,
∴,
∵∠POD=∠COD,
∴,
∴
∵
∴OP DM=3PD,
∴
∴
∵PD2=PM2+DM2,
∴
解得:t=16(不合题意,舍去),
∴当时,OD平分∠COP.
18.
(1)由题意可得,,,
在矩形中,
∵,,
,
在中,,
,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
∴.
答:为时,.
(2)过点作,交于点,
在等腰中,
,,
则.
∵,
∴,
∴四边形是矩形,
∴.
∵,
∴,
又∵,
∴,
∴,∴,∴.
∵,∴,
又∵,
∴,
∴,
∴,
∴,.
∴
.
答:与的函数关系式是.
(3)延长交于点,由(1),(2)可得,
,,
∵,
∴四边形是矩形,
∴,
同理可证,四边形是矩形.
∴,
当时,
∵,
∴,
∴.
又∵,
∴,
∴.
答:当时,.
(4)由(2)得,,
∵,,
∴,
∴为矩形,
∴,且.
∴,
∵,
∴,
同理可证,
∴,,
∴,
∴,
∴.
答:在运动的过程中,存在时刻,使.
19.
解:(1)结论:△ABC是“准黄金”三角形,BC是“金底”.
理由:过点A作AD⊥CB交CB的延长线于D.
∵AC=8,∠C=30°,
∴AD=4,
∴=
∴△ABC是“准黄金”三角形,BC是“金底”;
(2)如图,
∵A,D关于BC对称,
∴BE⊥AD,AE=ED,
∵△ABC是“准黄金”三角形,BC是“金底”,
∴=,不妨设AE=4k,BC=5k,
∵C是△ABD的重心,
∴BC:CE=2:1,
∴CE=,BE= ,
∴AB=,
∴;
(3)如图,过点A作AE⊥BC于E,过点D作DF⊥AC于F,过点B′作B′G⊥BC于G.
△ABC是“准黄金”三角形,
旋转
=CB=5,
∵∠CGB′=90°,GB′=4,
∴ ,
又∵=,
∴ ,
∴ ,
∴,
将△ABC绕点C按顺时针方向旋转得到△A′B′C
即∠GCB′=∠FCD,
∠CGB′=∠CFD=90°,
∴△CGB′∽△CFD,
∴DF:CF:CD=GB′:CG:CB′=3:4:5,
设DF=4k,CF=3k,CD=5k,
∵△AEC∽△DFA,
,
解得: ,
∴,
∴
.
20.
(1)证明:如图1,将ABE绕点A顺时针旋转90°,使AB与AD重合,得到了旋转后的ADG,
∴∠BAE=∠DAG,AE=AG,∠B=∠ADG=90°,BE=DG,
∴∠ADF+∠ADG=180°,
∴F,D,G三点共线,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠DAG+∠FAD=45°,
∴∠EAF=∠FAG,
在EAF与GAF中,
,
∴EAF≌GAF(SAS),
∴EF=FG,
∵DG+FD=FG,
∴BE+FD=EF;
(2)解:∵四边形ABCD为正方形,
∴AB=BC,∠B=∠C=∠A=∠D=90°,
∵BE=3,EC=2,
∴AB=BC=5,
∵翻折,
∴设AG=GE=x,则BG=5-x,
∵在RtBGE中,,
∴,
解得:,
∴,
∵翻折,
∴∠GEF=∠A=90°,
∴∠GEB+∠FEC=∠GEB+∠BGE=90°,
∴∠FEC=∠BGE,
又∵∠B=∠C,
∴,
∴,
即:,
解得:,
∴EF的长为;
(3)解:如图,连接AF,设∠FQA=∠FEA=m,
∵EF=EA,
∴∠EAF=∠EFA=,
∵∠FQA=∠FEA,∠FOQ=∠AOE,
∴,
∴,
∴,
又∵∠FOA=∠QOE,
∴,
∴∠AQE=∠AFE=,
∵∠CFQ=34°,∠C=90°,
∴∠CQF=90°-∠CFQ=56°,
∵∠CQF+∠FQA+∠AQE=180°,
∴56°+m+=180°,
解得:m=68°,
∵∠D=90°,
∴∠QAD=90°-∠AQE
=90°-()
=
=34°,
故答案为:34.
21.
(1)如图,连接BD,
在矩形ABCD中,∠DAB=90°,
∴BD是⊙O的直径,
∵⊙O半径为5,
∴BD=10,
∴AD= =6;
(2)如图,过点E作EG⊥AE交AF的延长线于点G,过点G作MN⊥AB,分别交直线DC、AB点M、N,
在矩形ABCD中,∠D=∠DAB=90°,
∴∠EMG=∠D=90°,
∴四边形ADMN是矩形,
∴∠EGM+∠MEG=90°,
∴∠AED+∠MEG=90°,
∴∠EGM=∠AED,
在△AEG中,∠EAF=45°,
∴∠EAF=∠EGF=45°,
∴AE=EG,
∴△AED≌△EGM(AAS),
∴MG=DE= ,EM=AD=6,
∴AN=DE+EM= ,NG=MN﹣MG= ,
∵MNADBC,
∴△ABF∽△ANG,
∴ ,
解得BF=2;
(3)△AEF的面积存在最小值,理由如下:
过点E作EH⊥AB于H,交AF于点P,作△APE的外接圆⊙I,连接IA、IP、IE,过I作IQ⊥CD于点Q,设⊙I的半径为r,
∵∠EAF=45°,
∴∠EIP=90°,∠IEP=45°,∠IEQ=45°,
∴EP= r,IQ=r,
∵IA+IQ≥AD,
∴r+r≥6,
∴r≥12﹣6 ,
∴S△AEF=AB EP=4r,
∴S△AEF≥4(12﹣6),
∴S△AEF ﹣48,
∴△AEF的面积存在最小值,最小值48﹣48.
22.
解:(1)如图所示,过点A作AD⊥BC于D,
由题意得:恰好经过点A时,∠PAC=90°,,
∵AB=AC=5cm,BC=8cm,
∴BD=CD=4cm,
∴,
∴,,
∴,
又∵,
∴,
解得,
∴当时,恰好经过点A;
(2)如图,过点A作AD⊥BC于D,
由题意得:∠PEC==90°,cm, ,
∴∠ADC=∠PEC=90°,
∵∠C=∠C,
∴△ADC∽△PEC,
∴,
∵,BD=CD=4cm,AD=3cm
∴,
∴,,
∴
∴
;
(3)存在,理由如下:
假设存在某一时刻,使平分,如图所示,过点Q作QH⊥BC于H,
∴∠QHC=∠QHB=∠QEP=∠ADC=90°
∴当平分时,EQ=QH(角平分线的性质),
∵∠C=∠C,
∴△ADC∽△QHC,
∴,
∴即,
∴,
由(2)得,
∴,
解得,
∴存在时,使平分;
(4)存在,理由如下:
假设存在,如图所示,当Q在PC的垂直平分线上时,
∴,
∵△ADC∽△QHC,
∴,
∴,
解得.
23.
(1)根据题意,
∵BC=8cm
∴
∵矩形ABCD
∴
∴
当时, 点P在AC的垂直平分线上
∴
∴
∴;
(2)根据题意,得:,
矩形ABCD面积
∵QE//AC
∴
∴
∴
∴
∴五边形APCEQ的面积矩形ABCD面积
∴;
(3)根据题意,△PQE是直角三角形,分,,三种情况;
当时,
∵QE//AC
∴
根据(1)的结论,当时,
∵
∴符合题意;
当时,
∵QE//AC
∴,交于点,如下图:
∴
∵
∴
∴,
∵AB=6cm,BC=8cm
∴
∴
∵
∴
∴
∴
∴
∵
∴符合题意,
当,点在矩形ABCD外
∴不成立;
∴当或时,可使△PQE是直角三角形.
24.
解:(1)将A(4,0),B(0,﹣4)的坐标代入y=ax2+b,
得 ,
解得, ,
∴抛物线的解析式为,
设直线CE为y=mx+n,将点E(4,﹣1),C(0,﹣3)的坐标代入y=mx+n得,
,
解得, ,
∴直线CE的解析式是;
(2)证明:设点,0<t<4,如图,过点P作PF⊥y轴于点F,
则PF=t, , , ,
所以 为定值;
(3)解:方法一:设DP与EC的交点为G,设,
①如图,当点G在点P上方时,
,
∵S△PEC=1 ,
∴,
解得: , (负根舍去),
∴ ,即 ,
②如图,当点G在点P下方时,
,
∵S△PEC=1,
∴ ,
解得: ,(负根舍去),
∴,即 ,
综上所述,满足条件的点有,.
方法二:如图,分别过点P,E作PF⊥CE,EH⊥y轴,垂足为F,H,PD交CE于点G,
在Rt△EHC中,EH=4,HC=2,
∴ ,
∵S△PEC=1,
∴ =1,
即 ,
∵PF⊥CE,PG⊥EH,
∴△PFG∽△CHE,
∴ ,
即 ,
解得 ,
∴过点P与直线CE平行,且与直线CE距离为 的直线有两条: 或 ,
依题意得: ,
解得: (负根舍去),
∴, ,
∴ ,
,
解得:(负根舍去),
∴, ,
∴,
综上所述,满足条件的点有,.
25.
证明:∵D,E分别是AB,AC的中点,
∴ ,
∵∠A=∠A,
∴△DAE∽△BAC,
∴∠ADE=∠B, ,
∴DE∥BC且DE=BC.
(1)证明:如图①连接AC,BD.
∵AM=BM,AQ=DQ,,
∴MQ=BD,同法可证PN=BD,PQ=MN=AC,
∵四边形ABCD是矩形,
∴AC=BD,
∴MQ=PQ=PN=MN,
∴四边形MNPQ是菱形.
(2)如图②:
连接BD,取DB的中点H,连接EH、FH,
∵F是BC边中点, E是AD的中点,
∴ , , ,
∴ ,
∵ ,
∴ ,
∴,
∴ ,
∴△EHF是等边三角形 .
∴ .
26.
证明:(1)∵四边形ABCD是平行四边形,
∴,且 ,
∴ ,
又∵ ,
∴,
∴ ,
∴ ,
∵,
∴BE AF=BC EF.
(2)∵AC⊥AB,四边形ABCD是平行四边形,
∴ ,
∵AE⊥BC ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵BE=3,AB=4,
∴在中, ,
∴ ,
∴ ,
∵四边形ABCD是平行四边形,
∴ ,, ,,
∴ ,
在中, ,
∴ ,
∴ ,
由(1)知,,
∴ ,
∴ ,
∴ ,
∴ .
一、单选题
1.如图,在中,,,是边上一点,且,连接,把沿翻折,得到,与交于点,连接,则的面积为( )
A. B. C. D.
2.如图,边长为10的等边中,点D在边上,且,将含角的直角三角板()绕直角顶点D旋转,分别交边于P、Q,连接,当时,的长为( )
A.6 B. C. D.
3.如图,在平面直角坐标系中,菱形的对称中心恰好是原点O,已知点B坐标是,双曲线经过点A,则菱形的面积是( )
A. B.18 C. D.25
4.如图,菱形的对角线与相交于点,,,点在上运动.过点作交于,交于点,将沿翻折得到,若,与重叠部分的面积为,下列图象能正确反映与的函数关系的是( )
A. B.
C. D.
5.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE·OP;③S△AOD=S四边形OECF;④当BP=1时,OE=. 其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系中,平行四边形的边交轴于点,反比例函数(,)的图象经过上的两点,.若,,平行四边形的面积为7,则的值为( )
A. B. C.2 D.
7.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是( )
A. B. C.2- D.-1
8.如图,在正方形ABCD中,,M是AD边上的一点,.将沿BM对折至,连接DN,则DN的长是( )
A. B. C.3 D.
二、填空题
9.如图,边长为5的圆内接正方形ABCD中,P为CD的中点,连按AP并延长交圆于点E,则DE的长为___.
10.如图,在平面直角坐标系中,反比例函数的图象过点,连接,过点作的垂线交反比例函数图象于另一点,若,点的横坐标为,则的值是_____________.
11.如图,在三角形中,点D为边的中点,连接,将三角形沿直线翻折至三角形平面内,使得B点与E点重合,连接、,分别与边交于点H,与交于点O,若,,,则点A到线段的距离为__________.
12.在中学数学中求一些图形面积时,经常用到“同底等高”“等底等高”等数学思想方法,我们称它为等积变换.如图,BD为的对角线,M、N分别在AD、AB上,且,若,则__________.
13.如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,设BE=x,则CF=____(用x表示);则GM的最小值为_____.
14.如图,是小明家客厅地面铺设的瓷砖图案,其中四边形是正方形,阴影部分是四个全等的菱形,且点A、E、F在同一条直线上.已知菱形较短的对角线长为,则正方形的面积为_________.
15.已知:正方形ABCD中,E为BC的中点,BP=2AP,F为AD上一点,EF交CP于O,∠POF=45°,若APF的面积为,则线段EF的长为___.
16.如图,已知,,的中垂线交于点D、交于点M.下列结论:①是的平分线:②是等腰三角形;③;④.正确的有_______.
三、解答题
17.已知,如图,在矩形ABCD中,,,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度也为1cm/s:当一个点停止运动时,另一个点也停止运动:联结PO并延长,交BC于点E,过点Q作,交BD与点F,设运动时间为.
(1)当t为何值时,是等腰三角形;
(2)设五边形OECQF的面积为,求S关于t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使OD平分 若存在求出t的值;若不存在,请说明理由.
18.已知:如图,在矩形和等腰中,,,.点从点出发,沿方向匀速运动.速度为;同时,点从点出发,沿方向匀速运动,速度为.过点作,交于点,交于点,过点作,交于点.分别连接,,设运动时间为.
解答下列问题:
(1)当时,求的值;
(2)设五边形的面积为,求与之间的函数关系式;
(3)当时,求的值;
(4)若与相交于点,分别连接和.在运动过程中,是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
19.(阅读)定义:如果一个三角形一条边上的高与这条边的比值是4:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(理解)(1)如图1,在△ABC中,AC=8,BC=5,∠ACB=30°,试判断△ABC是否是“准黄金”三角形,请说明理由.
(应用)(2)如图2,△ABC是“准黄金”三角形,BC是“金底”,把△ABC沿BC翻折得到△DBC,AD交BC的延长线于点E,若点C恰好是△ABD的重心,求的值.
(拓展)(3)如图3,a∥b,且直线a与b之间的距离为4,“准黄金”△ABC的“金底”BC在直线b上,点A在直线a上,=,若∠ABC是钝角,将△ABC绕点C按顺时针方向旋转得到△A′B′C,线段A′C交a于点D.当点B′落在直线b上时,求的值.
20.(1)问题背景:如图1,正方形ABCD中,F在直线CD上,E在直线BC上.若∠EAF=45°,求证:BE+FD=EF;
(2)迁移应用:如图2,将正方形ABCD的一部分沿GH翻折,使A点的对应点E在BC上,且AD的对应边EM交CD于F点.若BE=3,EC=2,求EF的长;
(3)联系拓展:如图3,正方形ABCD中,E、Q在CD上,F在BC上,若EF=EA,∠FQA=∠FEA.若∠CFQ=34°,则∠QAD=_______°.
21.如图,矩形ABCD是⊙O的内接矩形,⊙O半径为5,AB=8,点E、F分别是弦CD、BC上的动点,连结EF,∠EAF始终保持等于45°.
(1)求AD的长度.
(2)已知DE=,求BF的长度.
(3)试探究△AEF的面积是否存在最小值,若存在,请求出它的最小值;若不存在,请说明理由.
22.如图,等腰三角形的腰长,,动点从出发沿向运动,速度为,动点从出发沿向运动,速度为,当一个点到达终点时两个点同时停止运动.点是点关于直线的对称点,连接和,和相交于点.设运动时间为秒.
(1)若当的值是多少时,恰好经过点
(2)设的面积为,求与之间的函数关系式.
(3)是否存在某一时刻,使平分 若存在,求出相应的值,若不存在,请说明理由.
(4)是否存在某一时刻,使点在的垂直平分线上 若存在,求出相应的值,若不存在,请说明理由.
23.如图,已知:在矩形ABCD中,AB=6cm,BC=8cm,点P从点B出发,沿BC方向匀速运动,速度为2cm/s;与点P同时,点Q从D点出发,沿DA方向匀速运动,速度为1cm/s;过点Q作QE//AC,交DC于点E. 设运动时间为t (s),(0<t<4),解答下列问题:
(1)在运动过程中,是否存在某一时刻t,使点P在AC的垂直平分线上?若存在,求出t的值;若不存在,请说明理由;
(2)设五边形APCEQ的面积为y,求y与t的函数关系式:
(3)当0<t<时,是否存在某一时刻t,使△PQE是直角三角形?若存在,求出t的值;若不存在,请说明理由.
24.抛物线y=ax2+b经过点A(4,0),B(0,﹣4),直线EC过点E(4,﹣1),C(0,﹣3),点P是抛物线上点A、B间的动点(不含端点A、B),过P作PD⊥x轴于点D,连接PC、PE.
(1)求抛物线与直线CE的解析式;
(2)求证:PC+PD为定值;
(3)若△PEC的面积为1,求满足条件的点P的坐标.
25.
如图,在△ABC中,点D、E分别是AB与AC的中点,可以猜想:DE∥BC且DE=BC.请用演绎推理给出证明.
(1)如图①,在矩形ABCD中,点M、N、P、Q分别为AB、BC、CD、DA的中点,顺次连结M、N、P、Q.求证:四边形MNPQ是菱形.
(2)如图②,在△ABC中,F是BC边中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=60°,则FE的长为 .
26.如图,平行四边形ABCD的对角线AC、BD交于点O,点E为边BC上一点,连接AE交BD于点F.
(1)求证:BE AF=BC EF;
(2)若AC⊥AB,AE⊥BC,BE=3,AB=4,求的值.
答案
一、单选题
B.B.C.A.C.A.A.D.
二、填空题
9.
10.
11.
12.7
13.,.
14.
15.
16.①②③.
三、解答题
17.
解:(1)∵在矩形ABCD中,AB=6cm,BC=8cm,∠ABC=90°,
∴AC=10,,点O到AD的距离为3,
当为等腰三角形时,分三种情况讨论:
当AP=PO=t时
过P作PM⊥AO,如图1所示:
∴,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ACD,
∴
∴,
∴;
②当;
③当时即点P与点D重合,.不合题意,舍去.
综上所述,当或5s时,为等腰三角形
(2)在矩形ABCD中,,,
∴
∵,
∴,
∴,
在矩形ABCD中,AD//BC, AO=CO,又得∠AOP=∠COE,
∴∠PAO=∠ECO,
∴△AOP≌COE,
∴AP=EC=t,
∴,
∴
(3)存在,理由如下:
如图3,过D作DM⊥PE于M,DN⊥AC于N,
在矩形ABCD中,,,
∴,
∵∠POD=∠COD,
∴,
∴
∵
∴OP DM=3PD,
∴
∴
∵PD2=PM2+DM2,
∴
解得:t=16(不合题意,舍去),
∴当时,OD平分∠COP.
18.
(1)由题意可得,,,
在矩形中,
∵,,
,
在中,,
,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
∴.
答:为时,.
(2)过点作,交于点,
在等腰中,
,,
则.
∵,
∴,
∴四边形是矩形,
∴.
∵,
∴,
又∵,
∴,
∴,∴,∴.
∵,∴,
又∵,
∴,
∴,
∴,
∴,.
∴
.
答:与的函数关系式是.
(3)延长交于点,由(1),(2)可得,
,,
∵,
∴四边形是矩形,
∴,
同理可证,四边形是矩形.
∴,
当时,
∵,
∴,
∴.
又∵,
∴,
∴.
答:当时,.
(4)由(2)得,,
∵,,
∴,
∴为矩形,
∴,且.
∴,
∵,
∴,
同理可证,
∴,,
∴,
∴,
∴.
答:在运动的过程中,存在时刻,使.
19.
解:(1)结论:△ABC是“准黄金”三角形,BC是“金底”.
理由:过点A作AD⊥CB交CB的延长线于D.
∵AC=8,∠C=30°,
∴AD=4,
∴=
∴△ABC是“准黄金”三角形,BC是“金底”;
(2)如图,
∵A,D关于BC对称,
∴BE⊥AD,AE=ED,
∵△ABC是“准黄金”三角形,BC是“金底”,
∴=,不妨设AE=4k,BC=5k,
∵C是△ABD的重心,
∴BC:CE=2:1,
∴CE=,BE= ,
∴AB=,
∴;
(3)如图,过点A作AE⊥BC于E,过点D作DF⊥AC于F,过点B′作B′G⊥BC于G.
△ABC是“准黄金”三角形,
旋转
=CB=5,
∵∠CGB′=90°,GB′=4,
∴ ,
又∵=,
∴ ,
∴ ,
∴,
将△ABC绕点C按顺时针方向旋转得到△A′B′C
即∠GCB′=∠FCD,
∠CGB′=∠CFD=90°,
∴△CGB′∽△CFD,
∴DF:CF:CD=GB′:CG:CB′=3:4:5,
设DF=4k,CF=3k,CD=5k,
∵△AEC∽△DFA,
,
解得: ,
∴,
∴
.
20.
(1)证明:如图1,将ABE绕点A顺时针旋转90°,使AB与AD重合,得到了旋转后的ADG,
∴∠BAE=∠DAG,AE=AG,∠B=∠ADG=90°,BE=DG,
∴∠ADF+∠ADG=180°,
∴F,D,G三点共线,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠DAG+∠FAD=45°,
∴∠EAF=∠FAG,
在EAF与GAF中,
,
∴EAF≌GAF(SAS),
∴EF=FG,
∵DG+FD=FG,
∴BE+FD=EF;
(2)解:∵四边形ABCD为正方形,
∴AB=BC,∠B=∠C=∠A=∠D=90°,
∵BE=3,EC=2,
∴AB=BC=5,
∵翻折,
∴设AG=GE=x,则BG=5-x,
∵在RtBGE中,,
∴,
解得:,
∴,
∵翻折,
∴∠GEF=∠A=90°,
∴∠GEB+∠FEC=∠GEB+∠BGE=90°,
∴∠FEC=∠BGE,
又∵∠B=∠C,
∴,
∴,
即:,
解得:,
∴EF的长为;
(3)解:如图,连接AF,设∠FQA=∠FEA=m,
∵EF=EA,
∴∠EAF=∠EFA=,
∵∠FQA=∠FEA,∠FOQ=∠AOE,
∴,
∴,
∴,
又∵∠FOA=∠QOE,
∴,
∴∠AQE=∠AFE=,
∵∠CFQ=34°,∠C=90°,
∴∠CQF=90°-∠CFQ=56°,
∵∠CQF+∠FQA+∠AQE=180°,
∴56°+m+=180°,
解得:m=68°,
∵∠D=90°,
∴∠QAD=90°-∠AQE
=90°-()
=
=34°,
故答案为:34.
21.
(1)如图,连接BD,
在矩形ABCD中,∠DAB=90°,
∴BD是⊙O的直径,
∵⊙O半径为5,
∴BD=10,
∴AD= =6;
(2)如图,过点E作EG⊥AE交AF的延长线于点G,过点G作MN⊥AB,分别交直线DC、AB点M、N,
在矩形ABCD中,∠D=∠DAB=90°,
∴∠EMG=∠D=90°,
∴四边形ADMN是矩形,
∴∠EGM+∠MEG=90°,
∴∠AED+∠MEG=90°,
∴∠EGM=∠AED,
在△AEG中,∠EAF=45°,
∴∠EAF=∠EGF=45°,
∴AE=EG,
∴△AED≌△EGM(AAS),
∴MG=DE= ,EM=AD=6,
∴AN=DE+EM= ,NG=MN﹣MG= ,
∵MNADBC,
∴△ABF∽△ANG,
∴ ,
解得BF=2;
(3)△AEF的面积存在最小值,理由如下:
过点E作EH⊥AB于H,交AF于点P,作△APE的外接圆⊙I,连接IA、IP、IE,过I作IQ⊥CD于点Q,设⊙I的半径为r,
∵∠EAF=45°,
∴∠EIP=90°,∠IEP=45°,∠IEQ=45°,
∴EP= r,IQ=r,
∵IA+IQ≥AD,
∴r+r≥6,
∴r≥12﹣6 ,
∴S△AEF=AB EP=4r,
∴S△AEF≥4(12﹣6),
∴S△AEF ﹣48,
∴△AEF的面积存在最小值,最小值48﹣48.
22.
解:(1)如图所示,过点A作AD⊥BC于D,
由题意得:恰好经过点A时,∠PAC=90°,,
∵AB=AC=5cm,BC=8cm,
∴BD=CD=4cm,
∴,
∴,,
∴,
又∵,
∴,
解得,
∴当时,恰好经过点A;
(2)如图,过点A作AD⊥BC于D,
由题意得:∠PEC==90°,cm, ,
∴∠ADC=∠PEC=90°,
∵∠C=∠C,
∴△ADC∽△PEC,
∴,
∵,BD=CD=4cm,AD=3cm
∴,
∴,,
∴
∴
;
(3)存在,理由如下:
假设存在某一时刻,使平分,如图所示,过点Q作QH⊥BC于H,
∴∠QHC=∠QHB=∠QEP=∠ADC=90°
∴当平分时,EQ=QH(角平分线的性质),
∵∠C=∠C,
∴△ADC∽△QHC,
∴,
∴即,
∴,
由(2)得,
∴,
解得,
∴存在时,使平分;
(4)存在,理由如下:
假设存在,如图所示,当Q在PC的垂直平分线上时,
∴,
∵△ADC∽△QHC,
∴,
∴,
解得.
23.
(1)根据题意,
∵BC=8cm
∴
∵矩形ABCD
∴
∴
当时, 点P在AC的垂直平分线上
∴
∴
∴;
(2)根据题意,得:,
矩形ABCD面积
∵QE//AC
∴
∴
∴
∴
∴五边形APCEQ的面积矩形ABCD面积
∴;
(3)根据题意,△PQE是直角三角形,分,,三种情况;
当时,
∵QE//AC
∴
根据(1)的结论,当时,
∵
∴符合题意;
当时,
∵QE//AC
∴,交于点,如下图:
∴
∵
∴
∴,
∵AB=6cm,BC=8cm
∴
∴
∵
∴
∴
∴
∴
∵
∴符合题意,
当,点在矩形ABCD外
∴不成立;
∴当或时,可使△PQE是直角三角形.
24.
解:(1)将A(4,0),B(0,﹣4)的坐标代入y=ax2+b,
得 ,
解得, ,
∴抛物线的解析式为,
设直线CE为y=mx+n,将点E(4,﹣1),C(0,﹣3)的坐标代入y=mx+n得,
,
解得, ,
∴直线CE的解析式是;
(2)证明:设点,0<t<4,如图,过点P作PF⊥y轴于点F,
则PF=t, , , ,
所以 为定值;
(3)解:方法一:设DP与EC的交点为G,设,
①如图,当点G在点P上方时,
,
∵S△PEC=1 ,
∴,
解得: , (负根舍去),
∴ ,即 ,
②如图,当点G在点P下方时,
,
∵S△PEC=1,
∴ ,
解得: ,(负根舍去),
∴,即 ,
综上所述,满足条件的点有,.
方法二:如图,分别过点P,E作PF⊥CE,EH⊥y轴,垂足为F,H,PD交CE于点G,
在Rt△EHC中,EH=4,HC=2,
∴ ,
∵S△PEC=1,
∴ =1,
即 ,
∵PF⊥CE,PG⊥EH,
∴△PFG∽△CHE,
∴ ,
即 ,
解得 ,
∴过点P与直线CE平行,且与直线CE距离为 的直线有两条: 或 ,
依题意得: ,
解得: (负根舍去),
∴, ,
∴ ,
,
解得:(负根舍去),
∴, ,
∴,
综上所述,满足条件的点有,.
25.
证明:∵D,E分别是AB,AC的中点,
∴ ,
∵∠A=∠A,
∴△DAE∽△BAC,
∴∠ADE=∠B, ,
∴DE∥BC且DE=BC.
(1)证明:如图①连接AC,BD.
∵AM=BM,AQ=DQ,,
∴MQ=BD,同法可证PN=BD,PQ=MN=AC,
∵四边形ABCD是矩形,
∴AC=BD,
∴MQ=PQ=PN=MN,
∴四边形MNPQ是菱形.
(2)如图②:
连接BD,取DB的中点H,连接EH、FH,
∵F是BC边中点, E是AD的中点,
∴ , , ,
∴ ,
∵ ,
∴ ,
∴,
∴ ,
∴△EHF是等边三角形 .
∴ .
26.
证明:(1)∵四边形ABCD是平行四边形,
∴,且 ,
∴ ,
又∵ ,
∴,
∴ ,
∴ ,
∵,
∴BE AF=BC EF.
(2)∵AC⊥AB,四边形ABCD是平行四边形,
∴ ,
∵AE⊥BC ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵BE=3,AB=4,
∴在中, ,
∴ ,
∴ ,
∵四边形ABCD是平行四边形,
∴ ,, ,,
∴ ,
在中, ,
∴ ,
∴ ,
由(1)知,,
∴ ,
∴ ,
∴ ,
∴ .
同课章节目录
