九年级数学上册试题 4.6相似多边形 同步练习-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.6相似多边形 同步练习-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 391.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 11:26:47 | ||
图片预览

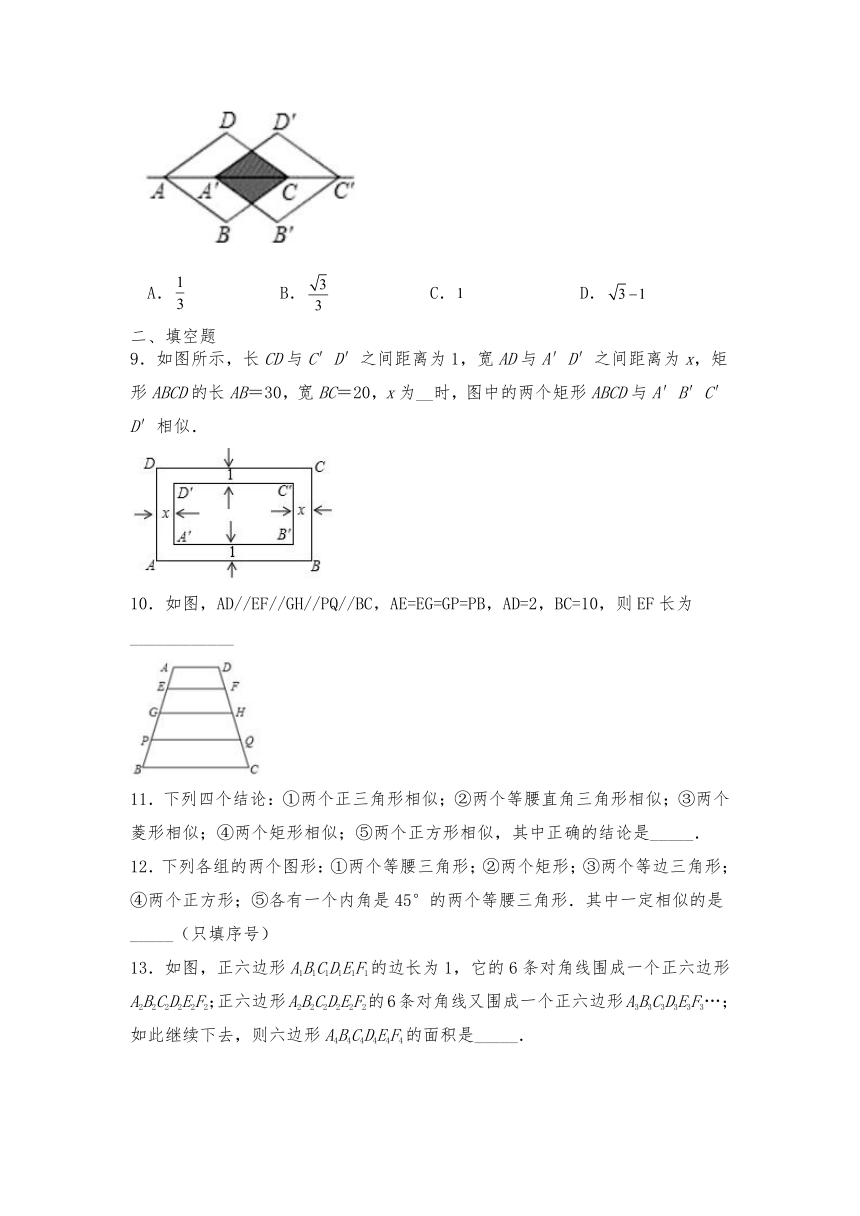
文档简介
4.6相似多边形
一、单选题
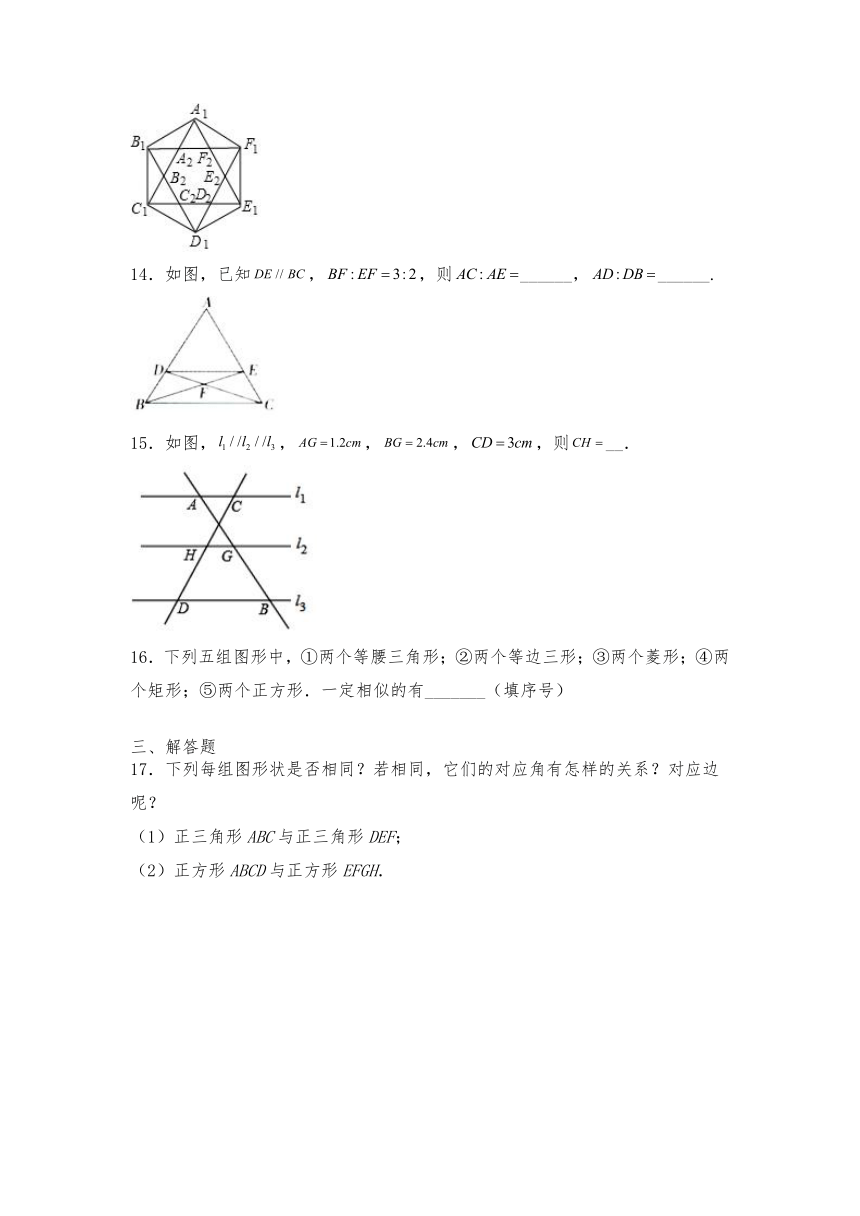
1.如图,矩形ABCD∽矩形BCFE,且AD=AE.则AB:AD的值是( )
A.:1 B.:1 C. D.
2.下列命题中,说法正确的个数是( )
(1)两个等边三角形一定相似;(2)有一个角相等的两个菱形一定相似;
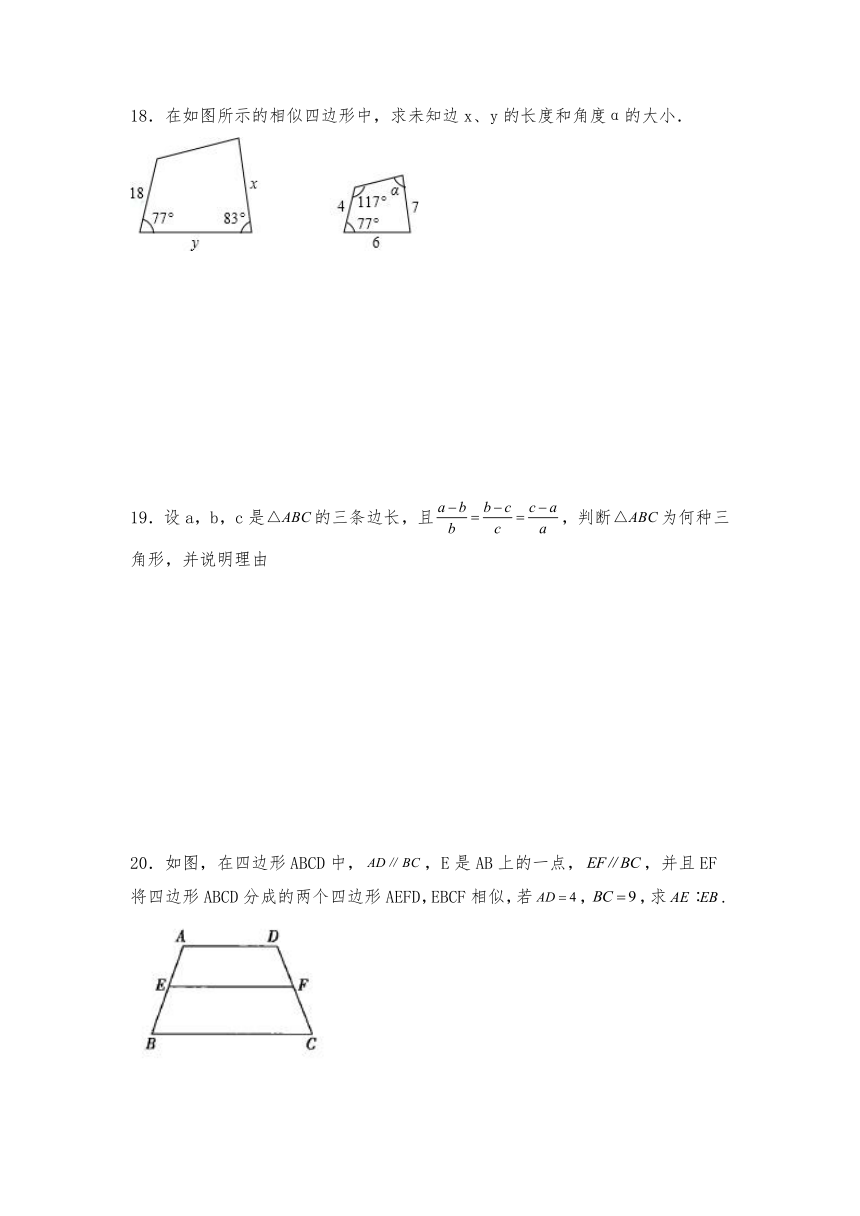
(3)两个等腰三角形腰上的高和腰对应成比例,则这两个三角形必相似;
(4)两边及第三边上的中线对应成比例的两三角形相似.
A.1个 B.2个 C.3个 D.4个
3.如图,矩形ABCD被分成5个正方形和2个小矩形后形成一个中心对称图形,如果矩形BEFG矩形ABCD,那么的值为( )
A. B. C. D.
4.若,则下列式子一定成立的是( )
A. B. C. D.
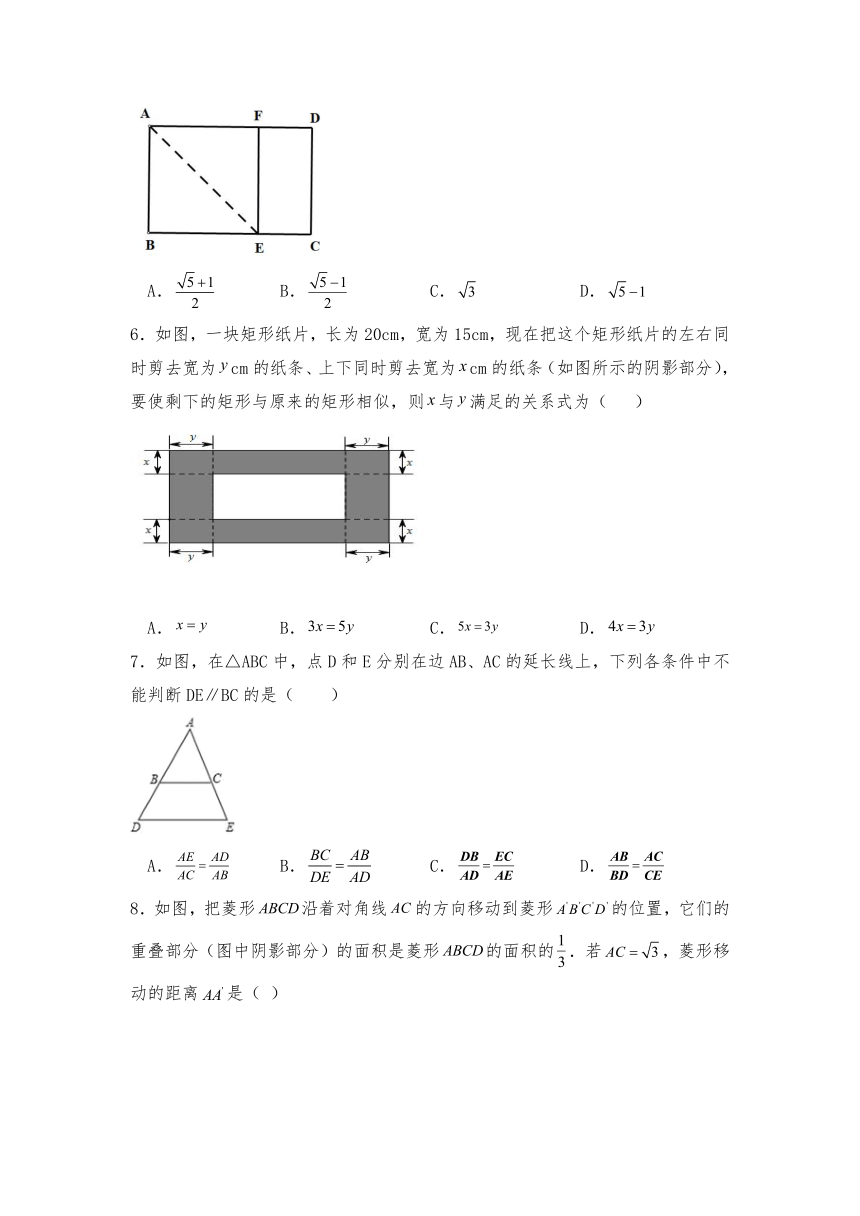
5.如图矩形中,,且,在上取一点,沿将向上折叠,使点落在上的点,若矩形与矩形相似,则( )
A. B. C. D.
6.如图,一块矩形纸片,长为20cm,宽为15cm,现在把这个矩形纸片的左右同时剪去宽为cm的纸条、上下同时剪去宽为cm的纸条(如图所示的阴影部分),要使剩下的矩形与原来的矩形相似,则与满足的关系式为( )
A. B. C. D.
7.如图,在△ABC中,点D和E分别在边AB、AC的延长线上,下列各条件中不能判断DE∥BC的是( )
A. B. C. D.
8.如图,把菱形沿着对角线的方向移动到菱形的位置,它们的重叠部分(图中阴影部分)的面积是菱形的面积的.若,菱形移动的距离是( )
A. B. C. D.
二、填空题
9.如图所示,长CD与C′D′之间距离为1,宽AD与A′D′之间距离为x,矩形ABCD的长AB=30,宽BC=20,x为__时,图中的两个矩形ABCD与A′B′C′D′相似.
10.如图,AD//EF//GH//PQ//BC,AE=EG=GP=PB,AD=2,BC=10,则EF长为____________
11.下列四个结论:①两个正三角形相似;②两个等腰直角三角形相似;③两个菱形相似;④两个矩形相似;⑤两个正方形相似,其中正确的结论是_____.
12.下列各组的两个图形:①两个等腰三角形;②两个矩形;③两个等边三角形;④两个正方形;⑤各有一个内角是45°的两个等腰三角形.其中一定相似的是_____(只填序号)
13.如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是_____.
14.如图,已知,,则______,______.
15.如图,,,,,则__.
16.下列五组图形中,①两个等腰三角形;②两个等边三形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有_______(填序号)
三、解答题
17.下列每组图形状是否相同?若相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形ABC与正三角形DEF;
(2)正方形ABCD与正方形EFGH.
18.在如图所示的相似四边形中,求未知边x、y的长度和角度α的大小.
19.设a,b,c是的三条边长,且,判断为何种三角形,并说明理由
20.如图,在四边形ABCD中,,E是AB上的一点,,并且EF将四边形ABCD分成的两个四边形AEFD,EBCF相似,若,,求.
21.已知:如图,Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,联结AE,点M为AE中点,联结BM,交AC于点G,联结MD,交CE于点H
(1)求证:MB=MD;
(2)当AB=BC,DC=DE时,求证:四边形MGCH为矩形.
22.已知,,,.求证:.
23.已知:如图,是等边外接圆的弧上一点,的延长线和的延长线相交于点,连接.
求证:(1);
(2).
24.如图,已知在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,且CF∶BC=4∶7,AB=14,求DB.
25.如图,矩形中,,把矩形沿对折,请你判断矩形与矩形相似吗?为什么?
26.已知四边形四边形,且,,,,,求,,,的长.
答案
一、单选题
C.D.C.A.A.D.B.D
二、填空题
9.1.5或9
10.4
11.①②⑤
12.③④;
13.
14. ,
15.
16.②⑤
三、解答题
17.
(1)正△ABC与正△DEF的形状相同.它们的对应角相等,都是60°.根据正三角形的边长相等可以得到对应边的比相等.
(2)正方形ABCD与正方形EFGH的形状相同.它们的对应角相等,都是90°.根据正方形的边长相等可以得到对应边的比相等.
18.
由于两个四边形相似,它们的对应边成比例,对应角相等,
所以==,解得x=31.5,y=27.
a=360°﹣(77°+83°+117°)=83°.
19.
解:为等边三角形.理由如下:
因为,所以由比例的性质可得,
,
因为a,b,c是的三条边长,
所以a>0,b>0,c>0,
所以,,,
所以,故为等边三角形.
20.
解:∵四边形AEFD与四边形EBCF相似,
∴,
又∵,,
∴.
又∵,
∴,
∴.
21.
证明:(1)延长BM交DE的延长线于N,如图,
∵∠ABC=∠CDE=90°,
∴AB∥DN,
∴=,
而点M为AE中点,
∴AM=ME,
∴BM=MN,
∴DM为Rt△BDN的斜边上的中线,
∴MB=MD;
(2)∵AB∥NE,
∴==1,即AB=NE,
∵AB=BC,DC=DE,
∴BD=BC+CD=AB+DE=NE+DE=DN,
∴△BDN为等腰直角三角形,
∴DM⊥BN,∠DBN=∠N=45°,∠BMD=90°,
∵AB=BC,DC=DE,
∴Rt△ABC和Rt△CDE都是等腰直角三角形,
∴∠CED=∠ACB=∠45°,
∴∠CED=∠N,∠ACB=∠BDM,
∴CE∥BN,AC∥DM,
∴四边形MGCH为平行四边形,
而∠GMH=90°,
∴四边形MGCH为矩形.
22.
∵,
∴,
∵,
∴,
∴,
∴,
∴.
23.
∵为等边三角形,
∴.
∴,
∵四边形为圆内接四边形,
∴,
∴,
∴,
又∵,
∴,
∴;
由知,
∴,
又∵,
∴.
24.
∵EF∥AB,且CF∶BC=4∶7,AB=14,
∴EF∶AB=CF∶BC=4∶7,即EF∶14=4∶7,
解得EF=8,
∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DB=EF=8.
25.
设BC=x,则AB=x,DF=x,===,由矩形的四个角都是90°,则矩形AEFD与矩形ABCD相似.
26.
解:∵四边形四边形,
∴,
即.
∴,,.
一、单选题
1.如图,矩形ABCD∽矩形BCFE,且AD=AE.则AB:AD的值是( )
A.:1 B.:1 C. D.
2.下列命题中,说法正确的个数是( )
(1)两个等边三角形一定相似;(2)有一个角相等的两个菱形一定相似;
(3)两个等腰三角形腰上的高和腰对应成比例,则这两个三角形必相似;
(4)两边及第三边上的中线对应成比例的两三角形相似.
A.1个 B.2个 C.3个 D.4个
3.如图,矩形ABCD被分成5个正方形和2个小矩形后形成一个中心对称图形,如果矩形BEFG矩形ABCD,那么的值为( )
A. B. C. D.
4.若,则下列式子一定成立的是( )
A. B. C. D.
5.如图矩形中,,且,在上取一点,沿将向上折叠,使点落在上的点,若矩形与矩形相似,则( )
A. B. C. D.
6.如图,一块矩形纸片,长为20cm,宽为15cm,现在把这个矩形纸片的左右同时剪去宽为cm的纸条、上下同时剪去宽为cm的纸条(如图所示的阴影部分),要使剩下的矩形与原来的矩形相似,则与满足的关系式为( )
A. B. C. D.
7.如图,在△ABC中,点D和E分别在边AB、AC的延长线上,下列各条件中不能判断DE∥BC的是( )
A. B. C. D.
8.如图,把菱形沿着对角线的方向移动到菱形的位置,它们的重叠部分(图中阴影部分)的面积是菱形的面积的.若,菱形移动的距离是( )
A. B. C. D.
二、填空题
9.如图所示,长CD与C′D′之间距离为1,宽AD与A′D′之间距离为x,矩形ABCD的长AB=30,宽BC=20,x为__时,图中的两个矩形ABCD与A′B′C′D′相似.
10.如图,AD//EF//GH//PQ//BC,AE=EG=GP=PB,AD=2,BC=10,则EF长为____________
11.下列四个结论:①两个正三角形相似;②两个等腰直角三角形相似;③两个菱形相似;④两个矩形相似;⑤两个正方形相似,其中正确的结论是_____.
12.下列各组的两个图形:①两个等腰三角形;②两个矩形;③两个等边三角形;④两个正方形;⑤各有一个内角是45°的两个等腰三角形.其中一定相似的是_____(只填序号)
13.如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是_____.
14.如图,已知,,则______,______.
15.如图,,,,,则__.
16.下列五组图形中,①两个等腰三角形;②两个等边三形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有_______(填序号)
三、解答题
17.下列每组图形状是否相同?若相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形ABC与正三角形DEF;
(2)正方形ABCD与正方形EFGH.
18.在如图所示的相似四边形中,求未知边x、y的长度和角度α的大小.
19.设a,b,c是的三条边长,且,判断为何种三角形,并说明理由
20.如图,在四边形ABCD中,,E是AB上的一点,,并且EF将四边形ABCD分成的两个四边形AEFD,EBCF相似,若,,求.
21.已知:如图,Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,联结AE,点M为AE中点,联结BM,交AC于点G,联结MD,交CE于点H
(1)求证:MB=MD;
(2)当AB=BC,DC=DE时,求证:四边形MGCH为矩形.
22.已知,,,.求证:.
23.已知:如图,是等边外接圆的弧上一点,的延长线和的延长线相交于点,连接.
求证:(1);
(2).
24.如图,已知在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,且CF∶BC=4∶7,AB=14,求DB.
25.如图,矩形中,,把矩形沿对折,请你判断矩形与矩形相似吗?为什么?
26.已知四边形四边形,且,,,,,求,,,的长.
答案
一、单选题
C.D.C.A.A.D.B.D
二、填空题
9.1.5或9
10.4
11.①②⑤
12.③④;
13.
14. ,
15.
16.②⑤
三、解答题
17.
(1)正△ABC与正△DEF的形状相同.它们的对应角相等,都是60°.根据正三角形的边长相等可以得到对应边的比相等.
(2)正方形ABCD与正方形EFGH的形状相同.它们的对应角相等,都是90°.根据正方形的边长相等可以得到对应边的比相等.
18.
由于两个四边形相似,它们的对应边成比例,对应角相等,
所以==,解得x=31.5,y=27.
a=360°﹣(77°+83°+117°)=83°.
19.
解:为等边三角形.理由如下:
因为,所以由比例的性质可得,
,
因为a,b,c是的三条边长,
所以a>0,b>0,c>0,
所以,,,
所以,故为等边三角形.
20.
解:∵四边形AEFD与四边形EBCF相似,
∴,
又∵,,
∴.
又∵,
∴,
∴.
21.
证明:(1)延长BM交DE的延长线于N,如图,
∵∠ABC=∠CDE=90°,
∴AB∥DN,
∴=,
而点M为AE中点,
∴AM=ME,
∴BM=MN,
∴DM为Rt△BDN的斜边上的中线,
∴MB=MD;
(2)∵AB∥NE,
∴==1,即AB=NE,
∵AB=BC,DC=DE,
∴BD=BC+CD=AB+DE=NE+DE=DN,
∴△BDN为等腰直角三角形,
∴DM⊥BN,∠DBN=∠N=45°,∠BMD=90°,
∵AB=BC,DC=DE,
∴Rt△ABC和Rt△CDE都是等腰直角三角形,
∴∠CED=∠ACB=∠45°,
∴∠CED=∠N,∠ACB=∠BDM,
∴CE∥BN,AC∥DM,
∴四边形MGCH为平行四边形,
而∠GMH=90°,
∴四边形MGCH为矩形.
22.
∵,
∴,
∵,
∴,
∴,
∴,
∴.
23.
∵为等边三角形,
∴.
∴,
∵四边形为圆内接四边形,
∴,
∴,
∴,
又∵,
∴,
∴;
由知,
∴,
又∵,
∴.
24.
∵EF∥AB,且CF∶BC=4∶7,AB=14,
∴EF∶AB=CF∶BC=4∶7,即EF∶14=4∶7,
解得EF=8,
∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DB=EF=8.
25.
设BC=x,则AB=x,DF=x,===,由矩形的四个角都是90°,则矩形AEFD与矩形ABCD相似.
26.
解:∵四边形四边形,
∴,
即.
∴,,.
同课章节目录
