九年级数学上册试题 4.7图形的位似同步测试-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.7图形的位似同步测试-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 11:49:01 | ||
图片预览



文档简介
4.7图形的位似
一、单选题
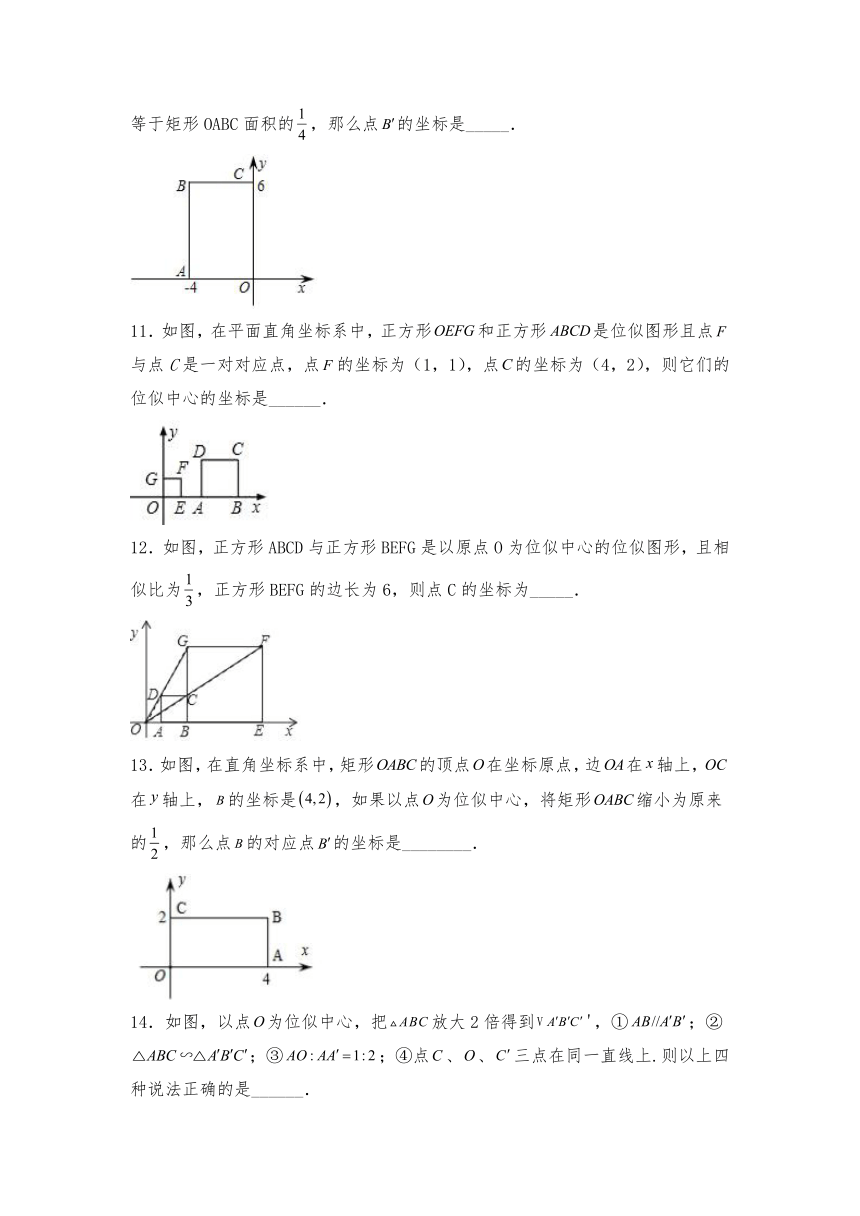
1.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )
A.1:2 B.2:1 C.1:3 D.3:1
2.如图,已知与位似,位似中心为点且的面积与面积之比为,则的值为( )
A. B. C. D.
3.如图,在平面直角坐标系中,已知点,以点为位似中心,将缩小为,其位似比为2:1,当反比例函数的图象经过的中点时,的值为( )
A. B.2 C.﹣1 D.
4.如图,已知□ABCD,以B为位似中心,作□ABCD的位似图形□EBFG,位似图形与原图形的位似比为,连结CG,DG.若□ABCD的面积为30,则△CDG的面积为( )
A.3 B.4 C.5 D.6
5.如图,△ABO与△CDO是以点O为位似中心的位似图形,若AB=4,AO=8,CO=2,则线段CD的长度为( )
A. B.1 C. D.2
6.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为,∠OCD=120°,CO=CD,若B(2,0),则点C的坐标为( )
A.(2,) B.(3,)
C.(3,) D.(,)
7.在平面直角坐标系中的位置如图所示,已知点A的坐标为,与关于点О成位似图形,且在点О的同一侧,与的位似比为1:2,则点A的对应点的坐标是( )
A. B. C. D.
8.如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )
A. B.﹣2 C. D.﹣3
二、填空题
9.如图,在平面直角坐标系中,已知点E(﹣4,2),F(﹣1,﹣1).以原点O为位似中心,把△EFO扩大到原来的2倍,则点E的对应点E'的坐标为_____.
10.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形与矩形OABC关于点O位似,且矩形的面积等于矩形OABC面积的,那么点的坐标是_____.
11.如图,在平面直角坐标系中,正方形和正方形是位似图形且点与点C是一对对应点,点的坐标为(1,1),点的坐标为(4,2),则它们的位似中心的坐标是______.
12.如图,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,正方形BEFG的边长为6,则点C的坐标为_____.
13.如图,在直角坐标系中,矩形的顶点在坐标原点,边在轴上,在轴上,的坐标是,如果以点为位似中心,将矩形缩小为原来的,那么点的对应点的坐标是________.
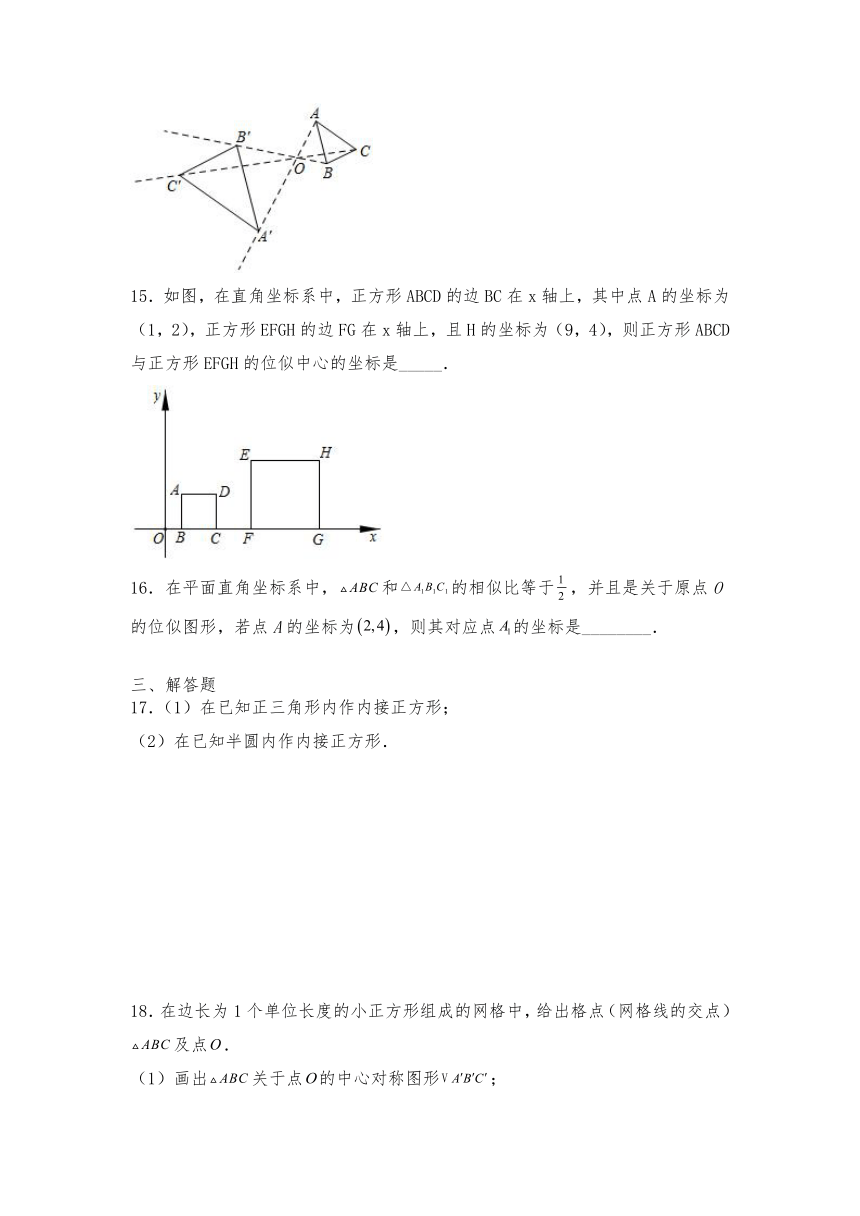
14.如图,以点为位似中心,把放大2倍得到',①;②;③;④点、、三点在同一直线上.则以上四种说法正确的是______.
15.如图,在直角坐标系中,正方形ABCD的边BC在x轴上,其中点A的坐标为(1,2),正方形EFGH的边FG在x轴上,且H的坐标为(9,4),则正方形ABCD与正方形EFGH的位似中心的坐标是_____.
16.在平面直角坐标系中,和的相似比等于,并且是关于原点O的位似图形,若点A的坐标为,则其对应点的坐标是________.
三、解答题
17.(1)在已知正三角形内作内接正方形;
(2)在已知半圆内作内接正方形.
18.在边长为1个单位长度的小正方形组成的网格中,给出格点(网格线的交点)及点.
(1)画出关于点的中心对称图形;
(2)以点为位似中心,画出将缩小为原来的后得到的(任意画出一个即可).
19.如图,的顶点都在方格线的交点(格点)上,按下列要求作答.
(1)以原点为位似中心,将放大为原来的倍,得到,请在所给的坐标系中作出一个满足条件的图形;
(2)写出你所画图形中,,点的坐标.
20.如图,在网格图中(小正方形的边长为1),的三个顶点都在格点上.
(1)把沿着轴向右平移6个单位得到,请你画出;
(2)请你以坐标系的原点点为位似中心在第一象限内画出的位似图形,使得与的位似比为1:2;
(3)请你直接写出三个顶点的坐标.
21.如图,请以A为位似中心,在A的右侧作△ADE,使△ADE∽△ABC,且位似比为2:1.(要求:尺规作图,保留作图痕迹,不写作法)
22.如图,在10×10的网格图内,建立如图所示的平面直角坐标系,△ABC的顶点坐标分别为A(﹣1,2)、B(2,3)、C(3,1).
(1)以原点O为位似中心,将△ABC按相似比2:1放大,得△A1B1C1,请画出△A1B1C1;
(2)以原点O为旋转中心,将△ABC按顺时针方向旋转90°,画出旋转后的△A2B2C2.直接写出点B到B2所经过的路径长 .
23.如图,已知一次函数y=ax+b与反比例函数的图象相交于点A(1,3)和B(m,1).
(1)求反比例函数与一次函数的表达式;
(2)根据图象回答,当x取何值时,反比例函数的值大于一次函数的值;
(3)以点O为位似中心画三角形,使它与△OAB位似,且相似比为2,请在图中画出所有符合条件的三角形.
24.如图.在平面直角坐标系内,三个顶点的坐标分别为(正方形网格中,每个小正方形的边长都是1个单位长度).
(1)作出向左平移5个单位长度,再向下平移3个单位长度得到的;
(2)以坐标原点O为位似中心,相似比为2,在第二象限内将放大,放大后得到作出.并求出中点D的坐标;
(3)以坐标原点O为旋转中心,将逆时针旋转,得到,作出.
25.如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中,每个小正方形的边长均是1个单位长度).
(1)△A1B1C1与△ABC关于x轴成轴对称,请画出△A1B1C1,并写出C1点的坐标;
(2)以点B1为位似中心,将△A1B1C1放大得到△A2B1C2,放大前后的面积之比为1:4,画出△A2B1C2,使它与△A1B1C1在位似中心同侧,并写出C2点的坐标;
(3)连接AC2、CC2,判断△ACC2的形状并直接写出结论.
26.如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)△ABC外接圆的半径是 ;
(2)已知△ABC与△DEF(点D、E、F都是格点)成位似图形,则位似中心M的坐标是 ;
(3)请在网格图中的空白处画一个格点△A1B1C1,使△A1B1C1∽△ABC,且相似比为:1.
答案
一、单选题
A.A.A.C.B.B.D.D.
二、填空题
9.(﹣8,4),(8,﹣4)
10.(﹣2,3)或(2,﹣3)
11.(-2,0)
12.(3,2)
13.或
14.①②④
15.(﹣3,0)或(,)
16.(4,8)或(﹣4,﹣8)
三、解答题
17.
解:(1)如图所示,正方形HIJK就是所求作正方形;
(2)如图所示,正方形HEFG就是所求作正方形;
18.
(1)根据题意,作图如下:
(2)根据结合(1)的结论,结合题意,作图如下:
19.
解:(1)如图所示;
(2)点,点,点或点,点,点
20.
解:(1)∵A(-3,0),B(-3,-2),C(-1,-3),
∴向右平移6个单位得到
(3,0),(3,-2),(5,-3),
如图所示;
(2)∵A(-3,0),B(-3,-2),C(-1,-3),
∴位似变化得到
(6,0),(6,4),(2,6),
如图所示;
(3)三个顶点的坐标分别为,,
21.
解:作图如下:
22.
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
OB,
所以点B到B2所经过的路径长π.
故答案为:π.
23.
解:(1)∵反比例函数y=(k≠0)图象经过A(1,3),
∴k=1×3=3,
∴反比例函数的表达式是y=,
∵反比例函数y=的图象过点B(m,1),
∴m=3,
∴B(3,1).
∵一次函数y=ax+b图象相交于A(1,3),B(3,1).
∴ ,
解得 ,
∴一次函数的表达式是y=﹣x+4;
(2)由图象知,当0<x<1或x>3时,反比例函数的值大于一次函数的值;
(3)如图所示△OA′B′和△OA″B″即为所求.
24.
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,
∵B2(-8,2),C2(-6,6),
∴D(,),即(-7,4);
(3)如图,△A3B3C3为所作.
25.
解:(1)由题意可得A、B、C三点关于x轴对称的点分别为:(0,-3)、(3,-4)、(2,-2),
给三点标上字母并依次连接即可得到所求作的图形,如下△A1B1C1为所作,
由上可得C1(2,﹣2);
(2)如图,△A2B2C2为所作,C2(1,0).
(3)∵AC2=12+22=5,CC22=12+22=5,AC22=12+32=10,
∴AC2+CC22=AC22,
∴△ACC2是等腰直角三角形.
26.
(1)如图,根据网格的特点分别作的垂直平分线,交于点,连接,根据网格的特点可知
则
△ABC外接圆的半径是,
故答案为:;
(2)如图,连接,交于点,,即位似中心,根据网格的特点可知
故答案为:;
(3)
△A1B1C1∽△ABC,且相似比为:1.
根据网格的特点作出,如图,
即为所求作的三角形.
一、单选题
1.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )
A.1:2 B.2:1 C.1:3 D.3:1
2.如图,已知与位似,位似中心为点且的面积与面积之比为,则的值为( )
A. B. C. D.
3.如图,在平面直角坐标系中,已知点,以点为位似中心,将缩小为,其位似比为2:1,当反比例函数的图象经过的中点时,的值为( )
A. B.2 C.﹣1 D.
4.如图,已知□ABCD,以B为位似中心,作□ABCD的位似图形□EBFG,位似图形与原图形的位似比为,连结CG,DG.若□ABCD的面积为30,则△CDG的面积为( )
A.3 B.4 C.5 D.6
5.如图,△ABO与△CDO是以点O为位似中心的位似图形,若AB=4,AO=8,CO=2,则线段CD的长度为( )
A. B.1 C. D.2
6.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为,∠OCD=120°,CO=CD,若B(2,0),则点C的坐标为( )
A.(2,) B.(3,)
C.(3,) D.(,)
7.在平面直角坐标系中的位置如图所示,已知点A的坐标为,与关于点О成位似图形,且在点О的同一侧,与的位似比为1:2,则点A的对应点的坐标是( )
A. B. C. D.
8.如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )
A. B.﹣2 C. D.﹣3
二、填空题
9.如图,在平面直角坐标系中,已知点E(﹣4,2),F(﹣1,﹣1).以原点O为位似中心,把△EFO扩大到原来的2倍,则点E的对应点E'的坐标为_____.
10.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形与矩形OABC关于点O位似,且矩形的面积等于矩形OABC面积的,那么点的坐标是_____.
11.如图,在平面直角坐标系中,正方形和正方形是位似图形且点与点C是一对对应点,点的坐标为(1,1),点的坐标为(4,2),则它们的位似中心的坐标是______.
12.如图,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,正方形BEFG的边长为6,则点C的坐标为_____.
13.如图,在直角坐标系中,矩形的顶点在坐标原点,边在轴上,在轴上,的坐标是,如果以点为位似中心,将矩形缩小为原来的,那么点的对应点的坐标是________.
14.如图,以点为位似中心,把放大2倍得到',①;②;③;④点、、三点在同一直线上.则以上四种说法正确的是______.
15.如图,在直角坐标系中,正方形ABCD的边BC在x轴上,其中点A的坐标为(1,2),正方形EFGH的边FG在x轴上,且H的坐标为(9,4),则正方形ABCD与正方形EFGH的位似中心的坐标是_____.
16.在平面直角坐标系中,和的相似比等于,并且是关于原点O的位似图形,若点A的坐标为,则其对应点的坐标是________.
三、解答题
17.(1)在已知正三角形内作内接正方形;
(2)在已知半圆内作内接正方形.
18.在边长为1个单位长度的小正方形组成的网格中,给出格点(网格线的交点)及点.
(1)画出关于点的中心对称图形;
(2)以点为位似中心,画出将缩小为原来的后得到的(任意画出一个即可).
19.如图,的顶点都在方格线的交点(格点)上,按下列要求作答.
(1)以原点为位似中心,将放大为原来的倍,得到,请在所给的坐标系中作出一个满足条件的图形;
(2)写出你所画图形中,,点的坐标.
20.如图,在网格图中(小正方形的边长为1),的三个顶点都在格点上.
(1)把沿着轴向右平移6个单位得到,请你画出;
(2)请你以坐标系的原点点为位似中心在第一象限内画出的位似图形,使得与的位似比为1:2;
(3)请你直接写出三个顶点的坐标.
21.如图,请以A为位似中心,在A的右侧作△ADE,使△ADE∽△ABC,且位似比为2:1.(要求:尺规作图,保留作图痕迹,不写作法)
22.如图,在10×10的网格图内,建立如图所示的平面直角坐标系,△ABC的顶点坐标分别为A(﹣1,2)、B(2,3)、C(3,1).
(1)以原点O为位似中心,将△ABC按相似比2:1放大,得△A1B1C1,请画出△A1B1C1;
(2)以原点O为旋转中心,将△ABC按顺时针方向旋转90°,画出旋转后的△A2B2C2.直接写出点B到B2所经过的路径长 .
23.如图,已知一次函数y=ax+b与反比例函数的图象相交于点A(1,3)和B(m,1).
(1)求反比例函数与一次函数的表达式;
(2)根据图象回答,当x取何值时,反比例函数的值大于一次函数的值;
(3)以点O为位似中心画三角形,使它与△OAB位似,且相似比为2,请在图中画出所有符合条件的三角形.
24.如图.在平面直角坐标系内,三个顶点的坐标分别为(正方形网格中,每个小正方形的边长都是1个单位长度).
(1)作出向左平移5个单位长度,再向下平移3个单位长度得到的;
(2)以坐标原点O为位似中心,相似比为2,在第二象限内将放大,放大后得到作出.并求出中点D的坐标;
(3)以坐标原点O为旋转中心,将逆时针旋转,得到,作出.
25.如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中,每个小正方形的边长均是1个单位长度).
(1)△A1B1C1与△ABC关于x轴成轴对称,请画出△A1B1C1,并写出C1点的坐标;
(2)以点B1为位似中心,将△A1B1C1放大得到△A2B1C2,放大前后的面积之比为1:4,画出△A2B1C2,使它与△A1B1C1在位似中心同侧,并写出C2点的坐标;
(3)连接AC2、CC2,判断△ACC2的形状并直接写出结论.
26.如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)△ABC外接圆的半径是 ;
(2)已知△ABC与△DEF(点D、E、F都是格点)成位似图形,则位似中心M的坐标是 ;
(3)请在网格图中的空白处画一个格点△A1B1C1,使△A1B1C1∽△ABC,且相似比为:1.
答案
一、单选题
A.A.A.C.B.B.D.D.
二、填空题
9.(﹣8,4),(8,﹣4)
10.(﹣2,3)或(2,﹣3)
11.(-2,0)
12.(3,2)
13.或
14.①②④
15.(﹣3,0)或(,)
16.(4,8)或(﹣4,﹣8)
三、解答题
17.
解:(1)如图所示,正方形HIJK就是所求作正方形;
(2)如图所示,正方形HEFG就是所求作正方形;
18.
(1)根据题意,作图如下:
(2)根据结合(1)的结论,结合题意,作图如下:
19.
解:(1)如图所示;
(2)点,点,点或点,点,点
20.
解:(1)∵A(-3,0),B(-3,-2),C(-1,-3),
∴向右平移6个单位得到
(3,0),(3,-2),(5,-3),
如图所示;
(2)∵A(-3,0),B(-3,-2),C(-1,-3),
∴位似变化得到
(6,0),(6,4),(2,6),
如图所示;
(3)三个顶点的坐标分别为,,
21.
解:作图如下:
22.
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
OB,
所以点B到B2所经过的路径长π.
故答案为:π.
23.
解:(1)∵反比例函数y=(k≠0)图象经过A(1,3),
∴k=1×3=3,
∴反比例函数的表达式是y=,
∵反比例函数y=的图象过点B(m,1),
∴m=3,
∴B(3,1).
∵一次函数y=ax+b图象相交于A(1,3),B(3,1).
∴ ,
解得 ,
∴一次函数的表达式是y=﹣x+4;
(2)由图象知,当0<x<1或x>3时,反比例函数的值大于一次函数的值;
(3)如图所示△OA′B′和△OA″B″即为所求.
24.
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,
∵B2(-8,2),C2(-6,6),
∴D(,),即(-7,4);
(3)如图,△A3B3C3为所作.
25.
解:(1)由题意可得A、B、C三点关于x轴对称的点分别为:(0,-3)、(3,-4)、(2,-2),
给三点标上字母并依次连接即可得到所求作的图形,如下△A1B1C1为所作,
由上可得C1(2,﹣2);
(2)如图,△A2B2C2为所作,C2(1,0).
(3)∵AC2=12+22=5,CC22=12+22=5,AC22=12+32=10,
∴AC2+CC22=AC22,
∴△ACC2是等腰直角三角形.
26.
(1)如图,根据网格的特点分别作的垂直平分线,交于点,连接,根据网格的特点可知
则
△ABC外接圆的半径是,
故答案为:;
(2)如图,连接,交于点,,即位似中心,根据网格的特点可知
故答案为:;
(3)
△A1B1C1∽△ABC,且相似比为:1.
根据网格的特点作出,如图,
即为所求作的三角形.
同课章节目录
