七年级数学上册试题 5.2等式的基本性质-浙教版(含答案)
文档属性
| 名称 | 七年级数学上册试题 5.2等式的基本性质-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 75.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 11:57:09 | ||
图片预览



文档简介
5.2等式的基本性质
一.选择题
1.如果x=y,那么根据等式的性质下列变形不正确的是( )
A.2﹣x=y﹣2 B.x+1=y+1 C.3x=3y D.
2.下列变形不正确的是( )
A.若a=b,则2a=a+b B.若 a=b,则a﹣b=0
C.若,则a=b D.若ac=bc,则a=b
3.根据等式的性质,下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.下列各组等式变形中,不一定成立的是( )
A.如果x=y,那么ax=ay B.如果,那么x=y
C.如果x﹣b=y﹣b,那么x=y D.如果x=y,那么
5.下列等式变形错误的是( )
A.由5x﹣7y=2,得﹣2﹣7y=5x
B.由6x﹣3=x+4,得6x﹣3=4+x
C.由8﹣x=x﹣5,得﹣x﹣x=﹣5﹣8
D.由x+9=3x﹣1,得3x﹣1=x+9
6.设x,y,z是实数,则下列判断正确的( )
A. B.若x=y,则 x+c=y﹣c
C.若x=y,则 D.若,则2x=3y
7.下列方程的变形,哪位同学计算结果正确的是( )
A.小明 B.小红 C.小英 D.小聪
8.宁宁同学拿了一个天平,测量饼干与糖果的质量(每块饼干的质量都相同,每颗糖果的质量都相同)做了一下试验.第一次:左盘放两块饼干,右盘放三颗糖果,结果天平平衡;第二次,左盘放一块饼干和一颗糖果,右盘放10克砝码,结果天平平衡;第三次:左盘放一颗糖果,右盘放一块饼干,下列哪一种方法可使天平再度平衡( )
A.左盘上加2克砝码 B.右盘上加2克砝码
C.左盘上加5克砝码 D.右盘上加5克砝码
二.填空题
9.已知5a+8b=3b+10,利用等式性质可求得a+b的值是 .
10.若5m﹣5n=1,则m﹣n=,这是依据 .
11.将方程4x+3y=6变形成用y的代数式表示x,则x= .
12.将等式3a﹣2b=2a﹣2b变形,过程如下:因为3a﹣2b=2a﹣2b,所以3a=2a(第一步),所以3=2(第二步),上述过程中,第一步的根据是 ,第二步得出了明显错误的结论,其原因是 .
13.小邱认为,若ac=bc,则a=b.你认为小邱的观点正确吗? (填“是”或“否”),并写出你的理由: .
14.阅读框图,在五个步骤中,依据等式的性质2的步骤有 (只填序号).
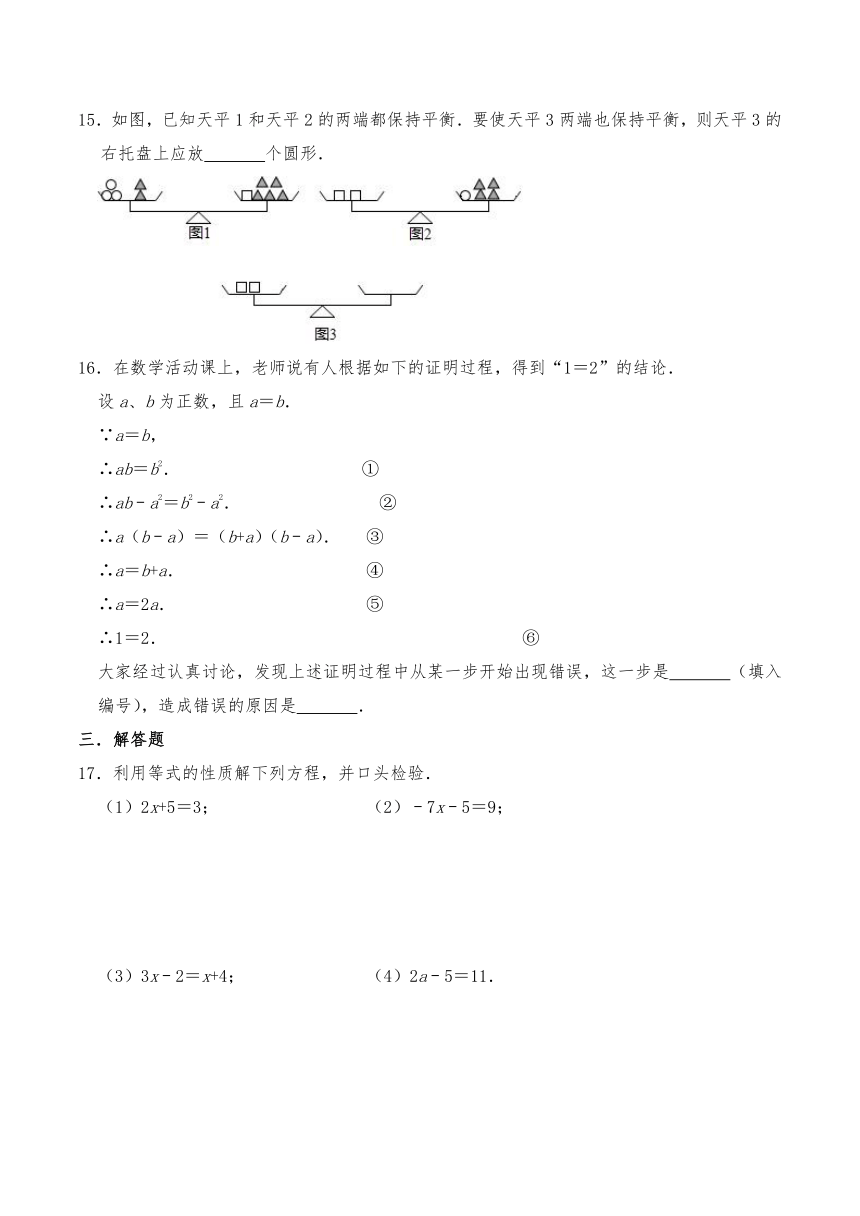
15.如图,已知天平1和天平2的两端都保持平衡.要使天平3两端也保持平衡,则天平3的右托盘上应放 个圆形.
16.在数学活动课上,老师说有人根据如下的证明过程,得到“1=2”的结论.
设a、b为正数,且a=b.
∵a=b,
∴ab=b2. ①
∴ab﹣a2=b2﹣a2. ②
∴a(b﹣a)=(b+a)(b﹣a). ③
∴a=b+a. ④
∴a=2a. ⑤
∴1=2. ⑥
大家经过认真讨论,发现上述证明过程中从某一步开始出现错误,这一步是 (填入编号),造成错误的原因是 .
三.解答题
17.利用等式的性质解下列方程,并口头检验.
(1)2x+5=3; (2)﹣7x﹣5=9;
(3)3x﹣2=x+4; (4)2a﹣5=11.
18.已知m﹣1=n,试用等式的性质比较m与n的大小.
19.已知当x=﹣2时,代数式ax2+bx+1的值为6,利用等式的性质求代数式﹣8a+4b的值.
20.老师在黑板上写了一个等式:(a+3)x=4(a+3).王聪说x=4,刘敏说不一定,当x≠4时,这个等式也可能成立.你认为他俩的说法正确吗?用等式的性质说明理由.
21.能不能由(a+3)x=b﹣1得到等式,为什么?反之,能不能由得到(a+3)x=b﹣1,为什么?
22.阅读下列材料:
问题:怎样将0.表示成分数?
小明的探究过程如下:
设x=0.①
10x=10×②
10x=8.③
10x=8④
10x=8+x⑤
9x=8⑥
⑦.
根据以上信息,回答下列问题:
(1)从步骤①到步骤②,变形的依据是 ;从步骤⑤到步骤⑥,变形的依据是 ;
(2)仿照上述探求过程,请你将0.表示成分数的形式.
答案
一.选择题
A.D.D.D.A.A.D.A.
二.填空题
9.2.
10.等式两边乘以同一个数或除以一个不为零的数,结果仍得等式.
11..
12.等式的基本性质1;没有考虑a=0的情况
13.否;当c=0时,a可以不等于b.
14.①⑤.
15.3.
16.④;等式两边除以值为零的式子,不符合等式性质.
三.解答题
17.解:(1)两边都减5,得
2x=﹣2,
两边都除以2,得
x=﹣1;
(2)两边都加5,得
﹣7x=14,
两边都除以﹣7,得
x=﹣2;
(3)两边都加(2﹣x),得
2x=6,
两边都除以2,得
x=3;
(4)两边都加5,得
2a=16,
两边都除以2,得
a=8.
18.解:已知等式去分母得:3m﹣4=3n,
整理得:3(m﹣n)=4,即m﹣n=>0,
∴m>n.
19.解:由题意,可得
4a﹣2b+1=6,
∴4a﹣2b=5,
∴﹣8a+4b
=﹣2(4a﹣2b)
=﹣2×5
=﹣10
20.解:王聪说x=4,不正确,
理由:当a+3=0时,x为任意实数;
刘敏说法正确,
理由:当a+3=0时,x为任意实数,当x≠4时,这个等式也可能成立.
21.解:不能由(a+3)x=b﹣1得到x=,
∵当a=﹣3时,a+3=0,而0不能为除数,即不符合等式的性质2的规定,
由x=可以得到(a+3)x=b﹣1,
∵x=是已知条件,已知条件中已经隐含着条件a+3≠0,等式两边同乘以一个数,等式仍成立.
22.解:(1)从步骤①到步骤②,变形的依据是:等式的基本性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等…
从步骤⑤到步骤⑥,变形的依据是:等式的基本性质1:等式两边加(或减)同一个数(或式子),结果仍相等.…
故答案为:等式的基本性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等;等式的基本性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
(2)设0.=x,…
100x=100×0.,…
100x=36.,
100x=36+x,…
99x=36,
. …
一.选择题
1.如果x=y,那么根据等式的性质下列变形不正确的是( )
A.2﹣x=y﹣2 B.x+1=y+1 C.3x=3y D.
2.下列变形不正确的是( )
A.若a=b,则2a=a+b B.若 a=b,则a﹣b=0
C.若,则a=b D.若ac=bc,则a=b
3.根据等式的性质,下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.下列各组等式变形中,不一定成立的是( )
A.如果x=y,那么ax=ay B.如果,那么x=y
C.如果x﹣b=y﹣b,那么x=y D.如果x=y,那么
5.下列等式变形错误的是( )
A.由5x﹣7y=2,得﹣2﹣7y=5x
B.由6x﹣3=x+4,得6x﹣3=4+x
C.由8﹣x=x﹣5,得﹣x﹣x=﹣5﹣8
D.由x+9=3x﹣1,得3x﹣1=x+9
6.设x,y,z是实数,则下列判断正确的( )
A. B.若x=y,则 x+c=y﹣c
C.若x=y,则 D.若,则2x=3y
7.下列方程的变形,哪位同学计算结果正确的是( )
A.小明 B.小红 C.小英 D.小聪
8.宁宁同学拿了一个天平,测量饼干与糖果的质量(每块饼干的质量都相同,每颗糖果的质量都相同)做了一下试验.第一次:左盘放两块饼干,右盘放三颗糖果,结果天平平衡;第二次,左盘放一块饼干和一颗糖果,右盘放10克砝码,结果天平平衡;第三次:左盘放一颗糖果,右盘放一块饼干,下列哪一种方法可使天平再度平衡( )
A.左盘上加2克砝码 B.右盘上加2克砝码
C.左盘上加5克砝码 D.右盘上加5克砝码
二.填空题
9.已知5a+8b=3b+10,利用等式性质可求得a+b的值是 .
10.若5m﹣5n=1,则m﹣n=,这是依据 .
11.将方程4x+3y=6变形成用y的代数式表示x,则x= .
12.将等式3a﹣2b=2a﹣2b变形,过程如下:因为3a﹣2b=2a﹣2b,所以3a=2a(第一步),所以3=2(第二步),上述过程中,第一步的根据是 ,第二步得出了明显错误的结论,其原因是 .
13.小邱认为,若ac=bc,则a=b.你认为小邱的观点正确吗? (填“是”或“否”),并写出你的理由: .
14.阅读框图,在五个步骤中,依据等式的性质2的步骤有 (只填序号).
15.如图,已知天平1和天平2的两端都保持平衡.要使天平3两端也保持平衡,则天平3的右托盘上应放 个圆形.
16.在数学活动课上,老师说有人根据如下的证明过程,得到“1=2”的结论.
设a、b为正数,且a=b.
∵a=b,
∴ab=b2. ①
∴ab﹣a2=b2﹣a2. ②
∴a(b﹣a)=(b+a)(b﹣a). ③
∴a=b+a. ④
∴a=2a. ⑤
∴1=2. ⑥
大家经过认真讨论,发现上述证明过程中从某一步开始出现错误,这一步是 (填入编号),造成错误的原因是 .
三.解答题
17.利用等式的性质解下列方程,并口头检验.
(1)2x+5=3; (2)﹣7x﹣5=9;
(3)3x﹣2=x+4; (4)2a﹣5=11.
18.已知m﹣1=n,试用等式的性质比较m与n的大小.
19.已知当x=﹣2时,代数式ax2+bx+1的值为6,利用等式的性质求代数式﹣8a+4b的值.
20.老师在黑板上写了一个等式:(a+3)x=4(a+3).王聪说x=4,刘敏说不一定,当x≠4时,这个等式也可能成立.你认为他俩的说法正确吗?用等式的性质说明理由.
21.能不能由(a+3)x=b﹣1得到等式,为什么?反之,能不能由得到(a+3)x=b﹣1,为什么?
22.阅读下列材料:
问题:怎样将0.表示成分数?
小明的探究过程如下:
设x=0.①
10x=10×②
10x=8.③
10x=8④
10x=8+x⑤
9x=8⑥
⑦.
根据以上信息,回答下列问题:
(1)从步骤①到步骤②,变形的依据是 ;从步骤⑤到步骤⑥,变形的依据是 ;
(2)仿照上述探求过程,请你将0.表示成分数的形式.
答案
一.选择题
A.D.D.D.A.A.D.A.
二.填空题
9.2.
10.等式两边乘以同一个数或除以一个不为零的数,结果仍得等式.
11..
12.等式的基本性质1;没有考虑a=0的情况
13.否;当c=0时,a可以不等于b.
14.①⑤.
15.3.
16.④;等式两边除以值为零的式子,不符合等式性质.
三.解答题
17.解:(1)两边都减5,得
2x=﹣2,
两边都除以2,得
x=﹣1;
(2)两边都加5,得
﹣7x=14,
两边都除以﹣7,得
x=﹣2;
(3)两边都加(2﹣x),得
2x=6,
两边都除以2,得
x=3;
(4)两边都加5,得
2a=16,
两边都除以2,得
a=8.
18.解:已知等式去分母得:3m﹣4=3n,
整理得:3(m﹣n)=4,即m﹣n=>0,
∴m>n.
19.解:由题意,可得
4a﹣2b+1=6,
∴4a﹣2b=5,
∴﹣8a+4b
=﹣2(4a﹣2b)
=﹣2×5
=﹣10
20.解:王聪说x=4,不正确,
理由:当a+3=0时,x为任意实数;
刘敏说法正确,
理由:当a+3=0时,x为任意实数,当x≠4时,这个等式也可能成立.
21.解:不能由(a+3)x=b﹣1得到x=,
∵当a=﹣3时,a+3=0,而0不能为除数,即不符合等式的性质2的规定,
由x=可以得到(a+3)x=b﹣1,
∵x=是已知条件,已知条件中已经隐含着条件a+3≠0,等式两边同乘以一个数,等式仍成立.
22.解:(1)从步骤①到步骤②,变形的依据是:等式的基本性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等…
从步骤⑤到步骤⑥,变形的依据是:等式的基本性质1:等式两边加(或减)同一个数(或式子),结果仍相等.…
故答案为:等式的基本性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等;等式的基本性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
(2)设0.=x,…
100x=100×0.,…
100x=36.,
100x=36+x,…
99x=36,
. …
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
