3.1直线与圆的位置关系(浙江省宁波市镇海区)
文档属性
| 名称 | 3.1直线与圆的位置关系(浙江省宁波市镇海区) |  | |
| 格式 | rar | ||
| 文件大小 | 315.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-08 20:44:00 | ||
图片预览


文档简介
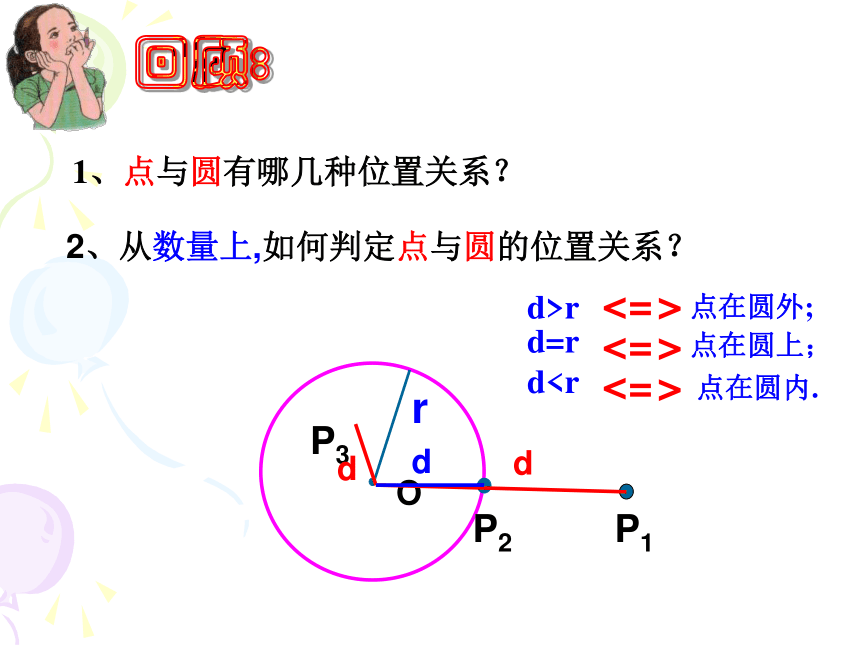
课件16张PPT。3.1 直线与圆的位置关系中兴中学 夏羽晶1、点与圆有哪几种位置关系?P1P2P32、从数量上,如何判定点与圆的位置关系?drdddr点在圆外;点在圆内. => => =><
<
<
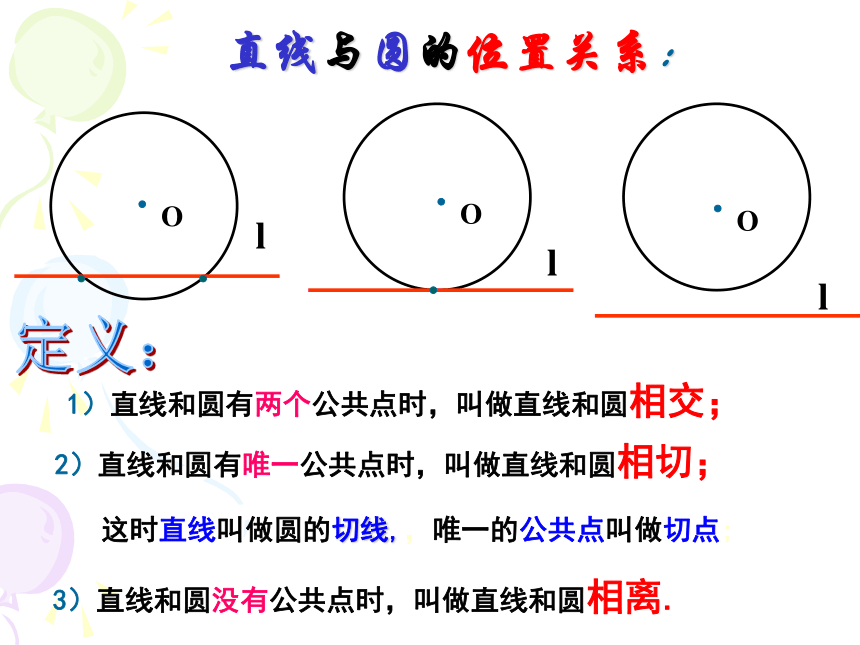
日出3)直线和圆没有公共点时,叫做直线和圆相离.lll直线与圆的位置关系: 2)直线和圆有唯一公共点时,叫做直线和圆相切; 1)直线和圆有两个公共点时,叫做直线和圆相交;定义: 这时直线叫做圆的切线,,唯一的公共点叫做切点;辨真伪,说理由:(1)当直线和圆相离时,直线和圆一定没有公共点。( ) √×(3)过⊙O内一点P作直线l,则直线l与⊙O相交。( )(4)过⊙O外一点P作直线l,则直线l与⊙O相切或相交。( )(5)过⊙O上一点p作直线l,则直线l与⊙O相切。( )(2)直线和圆有公共点时叫做直线和圆相切. ( )√××思考:如果圆心到直线的距离等于圆的直径,
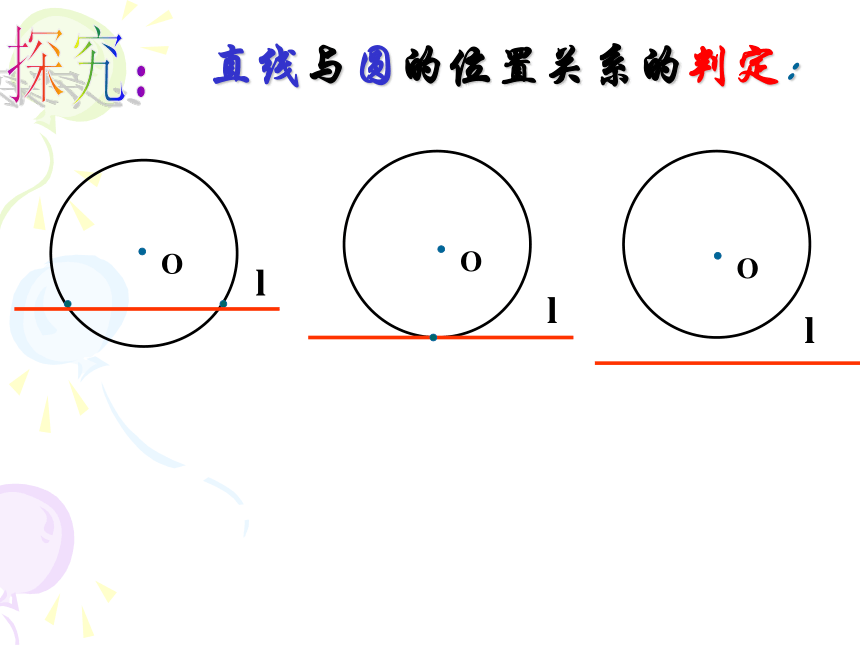
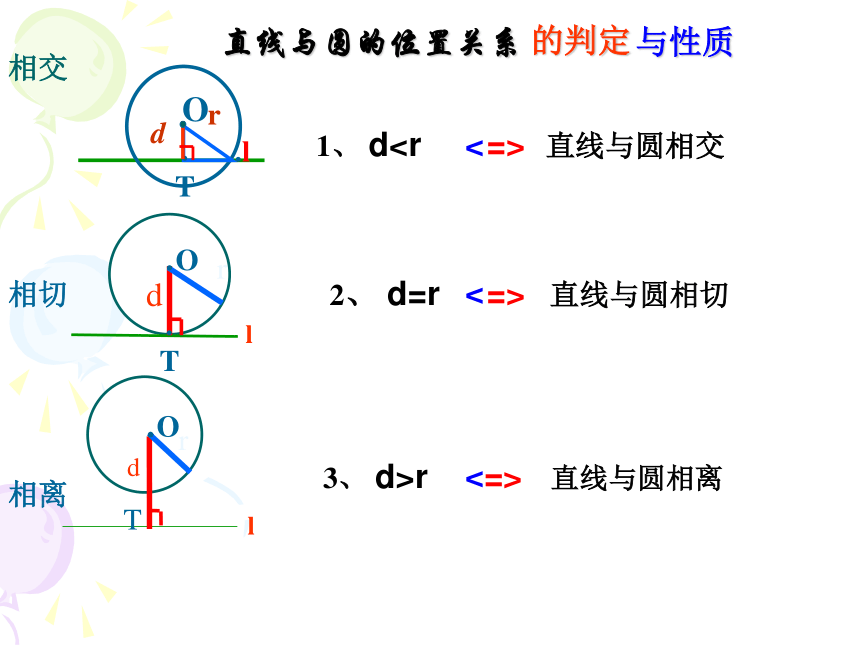
那么直线与圆有怎样的位置关系呢?lll直线与圆的位置关系的判定:探究:3、 d>r => 直线与圆相离2、 d=r => 直线与圆相切1、 d 直线与圆相交直线与圆的位置关系 的判定巩固: 设⊙O的半径为r,圆心O到直线L的距离为d,
根据下列条件判断直线L与⊙O的位置关系:
(1)d=4,r=3直线和圆的位置关系210dr交点切点无O?drOl?dr归纳:相交相切
相离 例1 已知Rt△ABC中,∠C=90°,AC=6㎝, BC=8cm,以点C为圆心,r为半径的圆与AB所在的直线有何位置关系?ACBD┛例题分析以点C为圆心,r为半径的圆与AB所在的直线有何位置关系?(1) r=4㎝; (2) r=4.8cm ; (3)r=6cm例2 在码头A的北偏东600方向有一个海岛, 离该岛中心P的12海里范围内是一个暗礁区. 货船从码头A由西向东方向航行,行驶10海里后到达点B,这时岛中心P在北偏东450方向.若货船不改变航向,问货船会不会进入暗礁区?要解决这个问题,我们首先将其数学化:
应用:感悟与反思本节课的学习你有哪些收获与体会?
一、知识上:1、直线与圆的三种位置关系:相交、相切和相离。2、直线与圆的位置关系的判定和性质:(1)定义:直线与圆的公共点的个数;(2)判定:圆心到直线的距离d与圆的半径r之间的大小关系。二、思想方法上:类比及转化的思想。如果该货船将一批重要物资运往M处,到达后必须立即卸货.此时,接到气象部门的通知,一台风中心正以40海里/小时的速度由N处(N在M的正西320海里处)向北偏西60°的方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响,问:
(1)M处是否会受到影响?
(2)若使该船不受台风影响,
应在多长时间内卸完货物?MNDFE拓展:C32030°⌒布置作业必做题:
1、课本P10――第1~5题;
2、作业本(1)P2――第1~4,
6(1)题。
选做题:
1、作业本(1)P2―第5、6
(2)~(4)题。
家庭作业
(2)做作业本(1)13页。(1)复习课本48--49页本节知识;课后思考:如何作圆的切线?再见!谢谢指导再见
<
<
日出3)直线和圆没有公共点时,叫做直线和圆相离.lll直线与圆的位置关系: 2)直线和圆有唯一公共点时,叫做直线和圆相切; 1)直线和圆有两个公共点时,叫做直线和圆相交;定义: 这时直线叫做圆的切线,,唯一的公共点叫做切点;辨真伪,说理由:(1)当直线和圆相离时,直线和圆一定没有公共点。( ) √×(3)过⊙O内一点P作直线l,则直线l与⊙O相交。( )(4)过⊙O外一点P作直线l,则直线l与⊙O相切或相交。( )(5)过⊙O上一点p作直线l,则直线l与⊙O相切。( )(2)直线和圆有公共点时叫做直线和圆相切. ( )√××思考:如果圆心到直线的距离等于圆的直径,
那么直线与圆有怎样的位置关系呢?lll直线与圆的位置关系的判定:探究:3、 d>r => 直线与圆相离2、 d=r => 直线与圆相切1、 d
根据下列条件判断直线L与⊙O的位置关系:
(1)d=4,r=3直线和圆的位置关系210d
相离 例1 已知Rt△ABC中,∠C=90°,AC=6㎝, BC=8cm,以点C为圆心,r为半径的圆与AB所在的直线有何位置关系?ACBD┛例题分析以点C为圆心,r为半径的圆与AB所在的直线有何位置关系?(1) r=4㎝; (2) r=4.8cm ; (3)r=6cm例2 在码头A的北偏东600方向有一个海岛, 离该岛中心P的12海里范围内是一个暗礁区. 货船从码头A由西向东方向航行,行驶10海里后到达点B,这时岛中心P在北偏东450方向.若货船不改变航向,问货船会不会进入暗礁区?要解决这个问题,我们首先将其数学化:
应用:感悟与反思本节课的学习你有哪些收获与体会?
一、知识上:1、直线与圆的三种位置关系:相交、相切和相离。2、直线与圆的位置关系的判定和性质:(1)定义:直线与圆的公共点的个数;(2)判定:圆心到直线的距离d与圆的半径r之间的大小关系。二、思想方法上:类比及转化的思想。如果该货船将一批重要物资运往M处,到达后必须立即卸货.此时,接到气象部门的通知,一台风中心正以40海里/小时的速度由N处(N在M的正西320海里处)向北偏西60°的方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响,问:
(1)M处是否会受到影响?
(2)若使该船不受台风影响,
应在多长时间内卸完货物?MNDFE拓展:C32030°⌒布置作业必做题:
1、课本P10――第1~5题;
2、作业本(1)P2――第1~4,
6(1)题。
选做题:
1、作业本(1)P2―第5、6
(2)~(4)题。
家庭作业
(2)做作业本(1)13页。(1)复习课本48--49页本节知识;课后思考:如何作圆的切线?再见!谢谢指导再见
