一次函数的小结与复习(1)

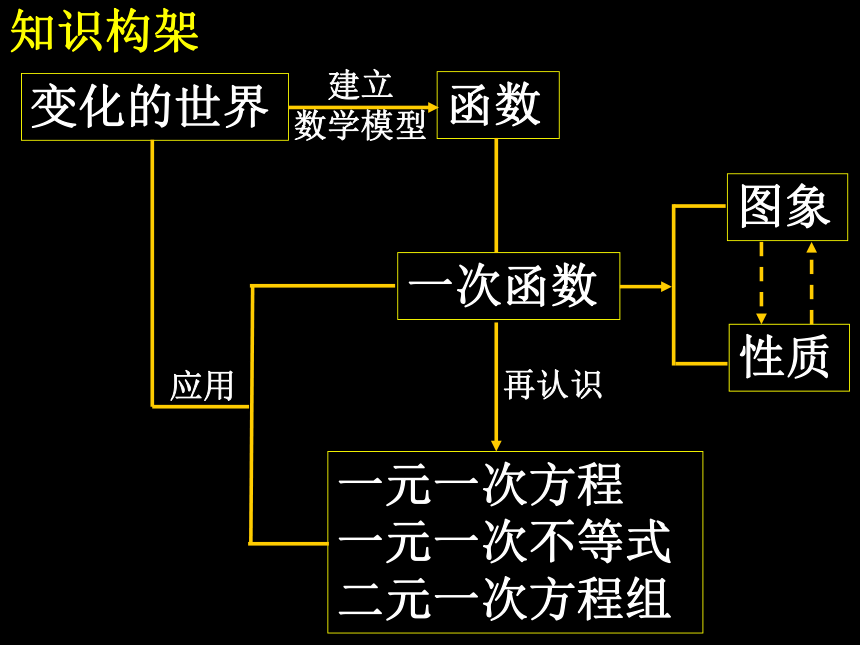
课件23张PPT。一次函数小结与复习知识构架变化的世界函数一次函数一元一次方程
一元一次不等式
二元一次方程组图象性质 建立
数学模型 应用 再认识典型例题函数定义例1、下表是我国人口的统计表：
若年份与人口分别记作x与y，则对于表中x的每一个确定的值，y都有唯一确定的对应值吗？当x =1989时，y的值是多少？两个变量的关系函数值的求法1、判断下列变量之间是否具有函数关系：
(1)长方形的长a一定时，它的面积s与宽b；
(2)一个正数a与它的平方根b；
(3)圆的面积s与它的半径r；
(4)人的年龄n与身高h。配套练习函数定义两个变量的关系典型例题例2、求函数 中自变量x的
取值范围。抽象函数：1、分母不为02、算术平方根的被开方数为非负数自变量的取值范围2、求函数 中自变量x的
取值范围。3、求函数 中自变量x的
取值范围。自变量的取值范围配套练习4、下表是我国人口的统计表：
写出y与x的函数解析式。1、上、下限2、取整实际意义函数：自变量的取值范围配套练习典型例题例3、函数 是一次函数，求m、n的取值。一次函数正比例函数一般式一次函数一般式一次函数的定义配套练习5、函数 是正比例函数，求m、n的取值。正比例函数一般式一次函数的定义典型例题例4、已知函数 是正比例函数，且y随x的增大而减小，
求m的取值范围。正比例函数的性质及位置过一、三象限过二、四象限递增递减配套练习一次函数的性质及位置6、已知函数 是一次函数，且y随x的增大而增大，求m的取值范围。过一、三、四象限过二、四、一象限过二、四、三象限过一、三、二象限递增递减7、下列图象中，不可能是关于 x 的
一次函数 的图象的
是( )x0yx0yx0yx0yABCD配套练习一次函数的性质及位置一次函数的性质及位置8、两直线 和
在同一平面直角坐标系内的图象可能
是 ( )配套练习假设找矛盾排除典型例题例5、已知函数 的图象经过
点A(0，2)，B(3，0)，求这个一次函数
的关系式。确定解析式待定系数法给出点坐标配套练习确定解析式9、一次函数的图象经过点(-2，-5)，
且与正比例函数 的图象交于
点Q(2，a)。
(1)求a的值；
(2)求一次函数的解析式；
(3)当x为何值时，一次函数的函数值
大于正比例函数的函数值？根据下列条件求一次函数的表达式:
(1).图象经过点A(0,3)且y=-2x+5与直线平行;
(2).图象与直线y=-2x+1交于y轴同一点,且经过点A(2,2);
(3).图象经过y=3x-6与x轴的交点，且平行于直线y=-5x-3;
(4).一次函数y=kx+3与坐标轴所围成的三角形的面积为6,求它的表达式.
典型例题变量与函数例1、均匀地向一个容器内注水，最后把容器注满。在注水过程中，水面高度h随时间t的变化规律如图所示，这个容器的形状是( )ABCABCD根据变化情况观察函数关系1、一天，亮亮感冒发烧了，早晨他烧得厉害，吃过药后感冒好多了，中午时亮亮的体温基本正常，但是下午他的体温又开始上升，直到半夜亮亮才感觉身上不那么发烫了．图中能基本反映出亮亮这一天(0～24时)体温的变化情况的是( )配套练习变量与函数根据图象观察函数关系2、已知正方形ABCD的边长是1,E为CD边的点,P为正方形ABCD边上的一个动点,动点P从A点出发,沿A→B→C→E运动,到达点E.若点P经过的路程为自变量x,△APE的面积为函数y,则当y=1/3时,x的值等于________.配套练习变量与函数根据实际意义求函数解析式列方程方法典型例题分段函数例2、在某火车站托运物品时，不超过
1千克的物品需付2元，以后每增加1千
克(不足1千克按1千克计)需增加托运
费5角，设托运p千克(p为整数)物品的费用为c元，写出c的计算公式。根据不同变化关系求分段函数解析式注明自变量取值范围配套练习3、某实验田的作物每天的需水量y(kg)
与生长时间x(天)之间的函数关系如折线
图所示，这些作物在第10天、第30天的
需水量分别为2000kg、3000kg，在第40
天后每天的需水量比前一天增加100kg。
(1)求出y与x之间的
函数关系式；分段函数配套练习3、某实验田的作物每天的需水量y(kg)
与生长时间x(天)之间的函数关系如折线
图所示，这些作物在第10天、第30天的
需水量分别为2000kg、3000kg，在第40
天后每天的需水量比前一天增加100kg。
(1)如果这些作物
每天的需水量大
于或等于4000kg
时需要进行人工灌
溉，那么从第几天开始进行人工灌溉？小结变化的世界函数一次函数一元一次方程
一元一次不等式
二元一次方程组图象性质 建立
数学模型 应用 再认识