九年级数学下册试题 3.4 简单几何体的表面展开图-浙教版(含答案)
文档属性
| 名称 | 九年级数学下册试题 3.4 简单几何体的表面展开图-浙教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 118.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 11:09:32 | ||
图片预览

文档简介
3.4 简单几何体的表面展开图
一.选择题
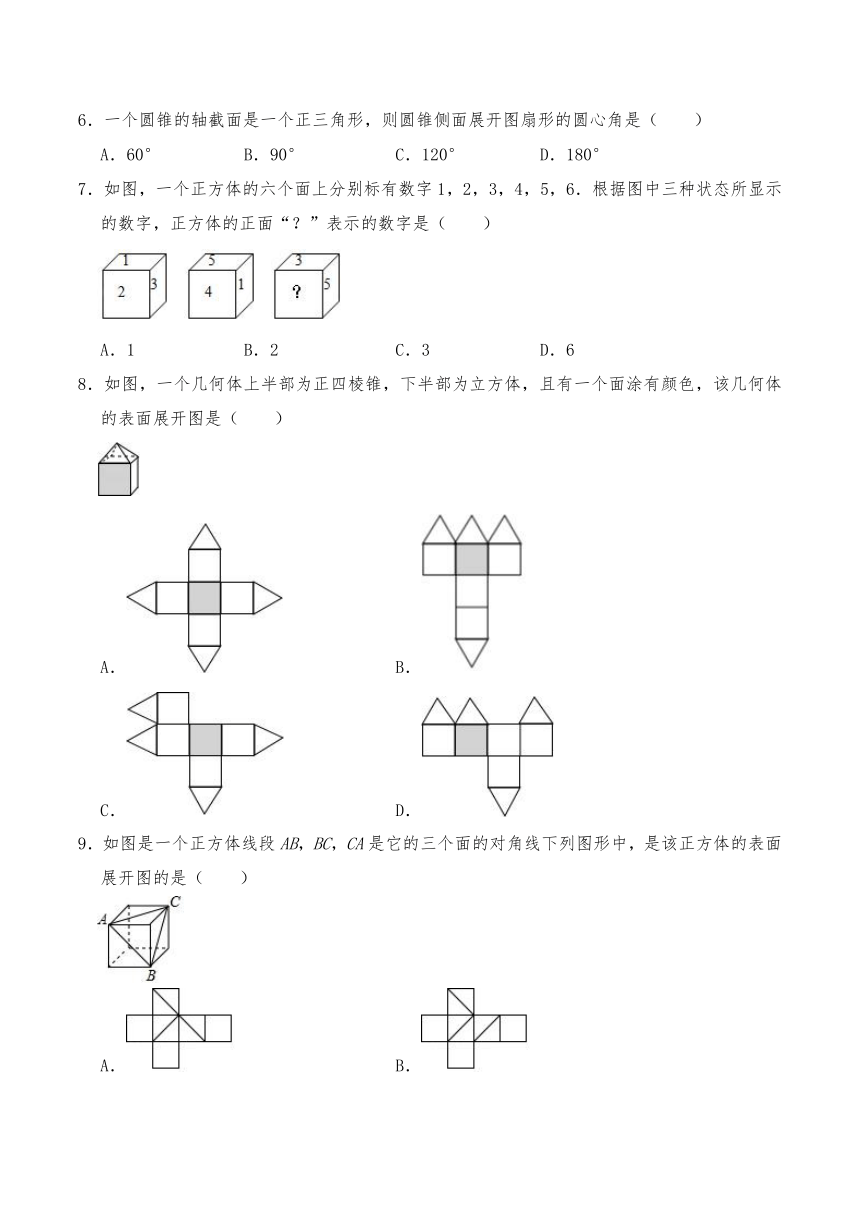
1.一个几何体的展开图如图所示,这个几何体是( )
A.圆锥 B.三棱锥 C.圆柱 D.四棱锥
2.下列不是正三棱柱的表面展开图的是( )
A. B. C. D.
3.如果圆锥的底面半径为3,母线长为6,那么它的侧面积等于( )
A.9π B.18π C.24π D.36π
4.如图是一个几何体的主视图和俯视图,则这个几何体是( )
A.正方体 B.三棱柱 C.三棱锥 D.长方体
5.下列图形中能折叠成棱柱的是( )
A. B.
C. D.
6.一个圆锥的轴截面是一个正三角形,则圆锥侧面展开图扇形的圆心角是( )
A.60° B.90° C.120° D.180°
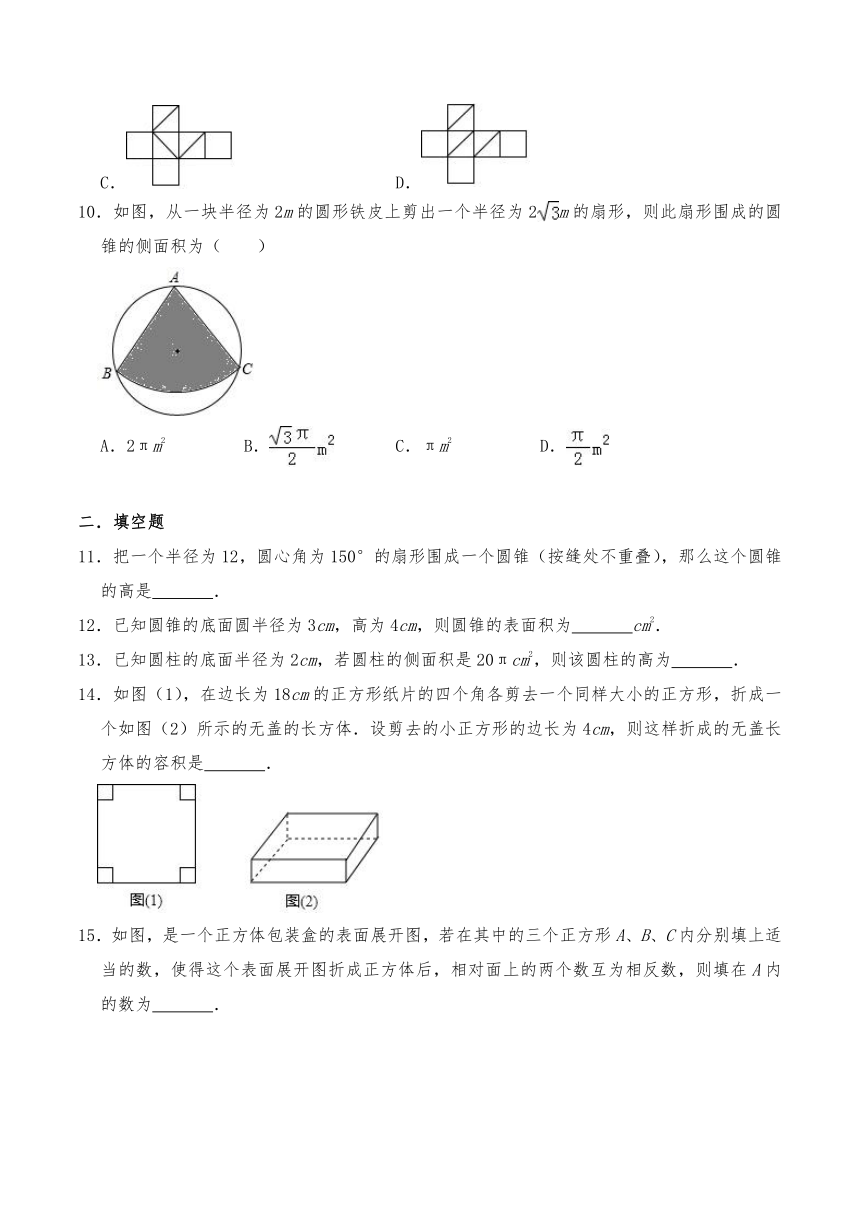
7.如图,一个正方体的六个面上分别标有数字1,2,3,4,5,6.根据图中三种状态所显示的数字,正方体的正面“?”表示的数字是( )
A.1 B.2 C.3 D.6
8.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A. B.
C. D.
9.如图是一个正方体线段AB,BC,CA是它的三个面的对角线下列图形中,是该正方体的表面展开图的是( )
A. B.
C. D.
10.如图,从一块半径为2m的圆形铁皮上剪出一个半径为2m的扇形,则此扇形围成的圆锥的侧面积为( )
A.2πm2 B. C.πm2 D.
二.填空题
11.把一个半径为12,圆心角为150°的扇形围成一个圆锥(按缝处不重叠),那么这个圆锥的高是 .
12.已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的表面积为 cm2.
13.已知圆柱的底面半径为2cm,若圆柱的侧面积是20πcm2,则该圆柱的高为 .
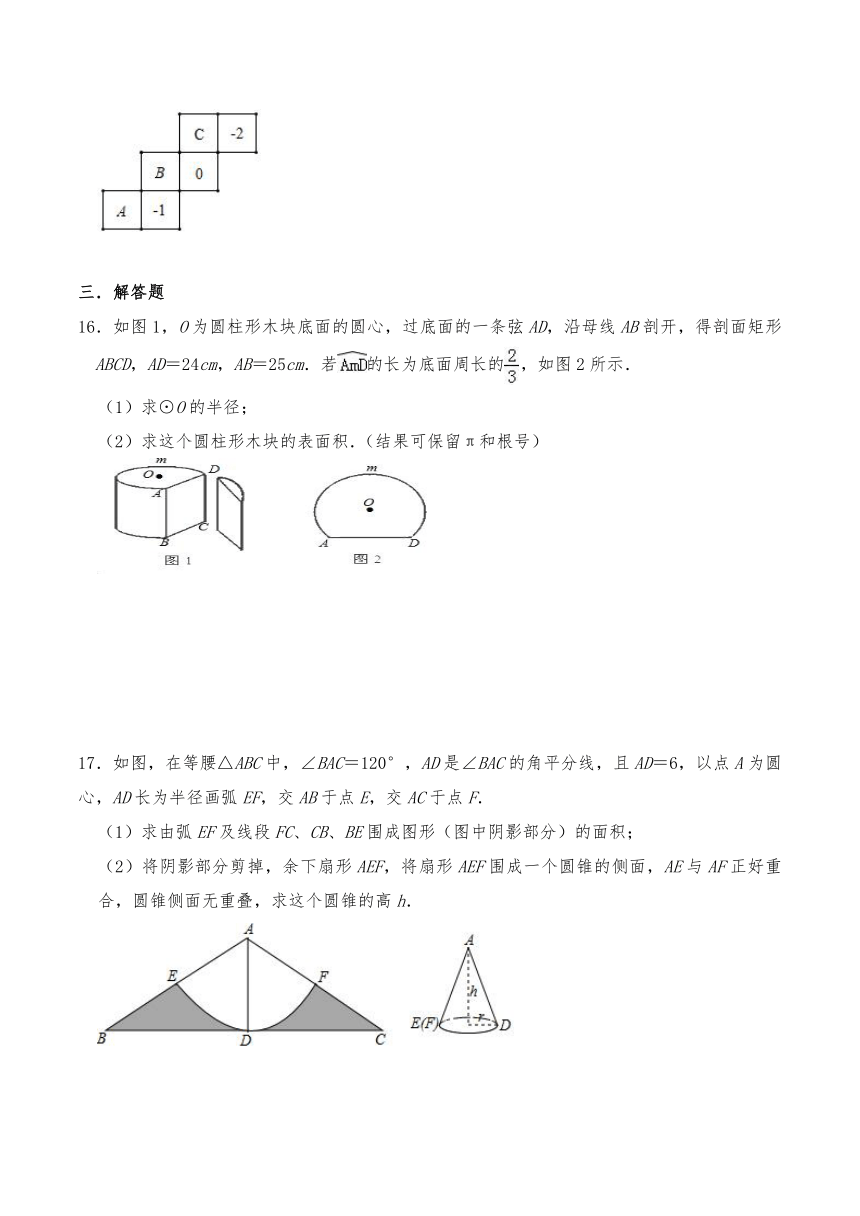
14.如图(1),在边长为18cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图(2)所示的无盖的长方体.设剪去的小正方形的边长为4cm,则这样折成的无盖长方体的容积是 .
15.如图,是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得这个表面展开图折成正方体后,相对面上的两个数互为相反数,则填在A内的数为 .
三.解答题
16.如图1,O为圆柱形木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.若的长为底面周长的,如图2所示.
(1)求⊙O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留π和根号)
17.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
18.如图是某涌泉蜜桔长方体包装盒的展开图.具体数据如图所示,且长方体盒子的长是宽的2倍.
(1)展开图的6个面分别标有如图所示的序号,若将展开图重新围成一个包装盒,则相对的面分别是 与 , 与 , 与 ;
(2)若设长方体的宽为xcm,则长方体的长为 cm,高为 cm;(用含x的式子表示)
(3)求这种长方体包装盒的体积.
19.如图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
20.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.
答案
一.选择题
C.D.B.B.B.D.D.B.C.A.
二.填空题
11..
12.24π.
13.5cm.
14.400cm2.
15.0.
三.解答题
16.解:(1)如图:连接OA,OD,过O作OE⊥AD,垂足为E,
∵由已知的长=圆周长,
∴扇形OAmD的圆心角为360°×=240°.
∠AOD=360°﹣240°=120°.
∵OE⊥AD,
∴∠AOE=120°=60°,AE=AD.
∵AD=24cm,
∴AE=12cm.
在Rt△AOE中,sin∠AOE=,
∴AO==(cm).
即⊙O的半径为cm.
(2)设圆柱的表面积为S,则S=2S圆+S侧,
2S圆=2π×(8)2=384π(cm2),
S侧=2π×8×25=400π(cm2),
∴S=(384+400)πcm2
答:木块的表面积为(384+400)πcm2.
17.解:∵在等腰△ABC中,∠BAC=120°,
∴∠B=30°,
∵AD是∠BAC的角平分线,
∴AD⊥BC,BD=CD,
∴BD=AD=6,
∴BC=2BD=12,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积=S△ABC﹣S扇形EAF=×6×12﹣=36﹣12π;
(2)设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4.
18.解:(1)展开图的6个面分别标有如图所示的序号,若将展开图重新围成一个包装盒,则相对的面分别是①与⑤,②与④,③与⑥;
故答案为:①;⑤;②;④;③;⑥;
(2)设长方体的宽为xcm,则长方体的长为cm,高为 cm,
故答案为:,;
(3)∵长是宽的2倍,
∴=2x,
解得:x=17,
∴这种长方体包装盒的体积=17×34×20=11560cm3,
答:这种长方体包装盒的体积是11560cm3.
19.解:(1)圆锥的高=,
底面圆的周长等于:2π×2=,
解得:n=120°;
(2)连结AC,过B作BD⊥AC于D,则∠ABD=60°.
由AB=6,可求得BD=3,
∴AD═3,
AC=2AD=6,
即这根绳子的最短长度是6.
20.解:(1)这个三棱柱有条9棱,有个5面;
故答案为:9,5;
(2)如图;
(3)由图形可知:没有剪开的棱的条数是4条,
则至少需要剪开的棱的条数是:9﹣4=5(条).
故至少需要剪开的棱的条数是5条.
需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).
故答案为:5,31.
一.选择题
1.一个几何体的展开图如图所示,这个几何体是( )
A.圆锥 B.三棱锥 C.圆柱 D.四棱锥
2.下列不是正三棱柱的表面展开图的是( )
A. B. C. D.
3.如果圆锥的底面半径为3,母线长为6,那么它的侧面积等于( )
A.9π B.18π C.24π D.36π
4.如图是一个几何体的主视图和俯视图,则这个几何体是( )
A.正方体 B.三棱柱 C.三棱锥 D.长方体
5.下列图形中能折叠成棱柱的是( )
A. B.
C. D.
6.一个圆锥的轴截面是一个正三角形,则圆锥侧面展开图扇形的圆心角是( )
A.60° B.90° C.120° D.180°
7.如图,一个正方体的六个面上分别标有数字1,2,3,4,5,6.根据图中三种状态所显示的数字,正方体的正面“?”表示的数字是( )
A.1 B.2 C.3 D.6
8.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A. B.
C. D.
9.如图是一个正方体线段AB,BC,CA是它的三个面的对角线下列图形中,是该正方体的表面展开图的是( )
A. B.
C. D.
10.如图,从一块半径为2m的圆形铁皮上剪出一个半径为2m的扇形,则此扇形围成的圆锥的侧面积为( )
A.2πm2 B. C.πm2 D.
二.填空题
11.把一个半径为12,圆心角为150°的扇形围成一个圆锥(按缝处不重叠),那么这个圆锥的高是 .
12.已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的表面积为 cm2.
13.已知圆柱的底面半径为2cm,若圆柱的侧面积是20πcm2,则该圆柱的高为 .
14.如图(1),在边长为18cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图(2)所示的无盖的长方体.设剪去的小正方形的边长为4cm,则这样折成的无盖长方体的容积是 .
15.如图,是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得这个表面展开图折成正方体后,相对面上的两个数互为相反数,则填在A内的数为 .
三.解答题
16.如图1,O为圆柱形木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.若的长为底面周长的,如图2所示.
(1)求⊙O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留π和根号)
17.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
18.如图是某涌泉蜜桔长方体包装盒的展开图.具体数据如图所示,且长方体盒子的长是宽的2倍.
(1)展开图的6个面分别标有如图所示的序号,若将展开图重新围成一个包装盒,则相对的面分别是 与 , 与 , 与 ;
(2)若设长方体的宽为xcm,则长方体的长为 cm,高为 cm;(用含x的式子表示)
(3)求这种长方体包装盒的体积.
19.如图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
20.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.
答案
一.选择题
C.D.B.B.B.D.D.B.C.A.
二.填空题
11..
12.24π.
13.5cm.
14.400cm2.
15.0.
三.解答题
16.解:(1)如图:连接OA,OD,过O作OE⊥AD,垂足为E,
∵由已知的长=圆周长,
∴扇形OAmD的圆心角为360°×=240°.
∠AOD=360°﹣240°=120°.
∵OE⊥AD,
∴∠AOE=120°=60°,AE=AD.
∵AD=24cm,
∴AE=12cm.
在Rt△AOE中,sin∠AOE=,
∴AO==(cm).
即⊙O的半径为cm.
(2)设圆柱的表面积为S,则S=2S圆+S侧,
2S圆=2π×(8)2=384π(cm2),
S侧=2π×8×25=400π(cm2),
∴S=(384+400)πcm2
答:木块的表面积为(384+400)πcm2.
17.解:∵在等腰△ABC中,∠BAC=120°,
∴∠B=30°,
∵AD是∠BAC的角平分线,
∴AD⊥BC,BD=CD,
∴BD=AD=6,
∴BC=2BD=12,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积=S△ABC﹣S扇形EAF=×6×12﹣=36﹣12π;
(2)设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4.
18.解:(1)展开图的6个面分别标有如图所示的序号,若将展开图重新围成一个包装盒,则相对的面分别是①与⑤,②与④,③与⑥;
故答案为:①;⑤;②;④;③;⑥;
(2)设长方体的宽为xcm,则长方体的长为cm,高为 cm,
故答案为:,;
(3)∵长是宽的2倍,
∴=2x,
解得:x=17,
∴这种长方体包装盒的体积=17×34×20=11560cm3,
答:这种长方体包装盒的体积是11560cm3.
19.解:(1)圆锥的高=,
底面圆的周长等于:2π×2=,
解得:n=120°;
(2)连结AC,过B作BD⊥AC于D,则∠ABD=60°.
由AB=6,可求得BD=3,
∴AD═3,
AC=2AD=6,
即这根绳子的最短长度是6.
20.解:(1)这个三棱柱有条9棱,有个5面;
故答案为:9,5;
(2)如图;
(3)由图形可知:没有剪开的棱的条数是4条,
则至少需要剪开的棱的条数是:9﹣4=5(条).
故至少需要剪开的棱的条数是5条.
需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).
故答案为:5,31.
