浙教版八年级数学下册试题 4.3 中心对称(含答案)
文档属性
| 名称 | 浙教版八年级数学下册试题 4.3 中心对称(含答案) | 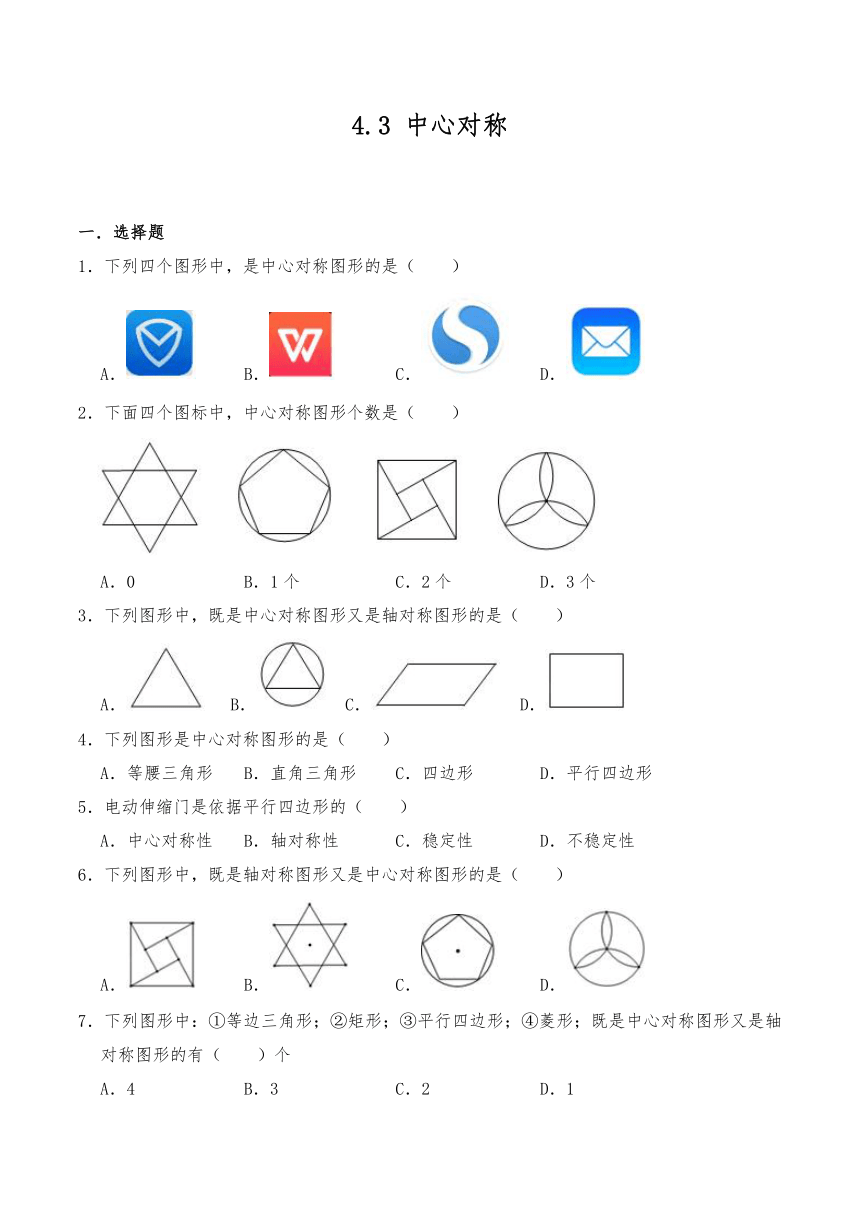 | |
| 格式 | docx | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 12:59:18 | ||
图片预览




文档简介
4.3 中心对称
一.选择题
1.下列四个图形中,是中心对称图形的是( )
A. B. C. D.
2.下面四个图标中,中心对称图形个数是( )
A.0 B.1个 C.2个 D.3个
3.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
4.下列图形是中心对称图形的是( )
A.等腰三角形 B.直角三角形 C.四边形 D.平行四边形
5.电动伸缩门是依据平行四边形的( )
A.中心对称性 B.轴对称性 C.稳定性 D.不稳定性
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
7.下列图形中:①等边三角形;②矩形;③平行四边形;④菱形;既是中心对称图形又是轴对称图形的有( )个
A.4 B.3 C.2 D.1
8.下列四张扑克牌中,左旋转180°后还是和原来一样的是( )
A. B. C. D.
9.如图将①②③④中的一块涂成阴影能与图中原有阴影部分组成中心对称图形的是( )
A.④ B.③ C.② D.①
二.填空题
10.若数字串“000”和数字串“101”既是轴对称图形,又是中心对称图形,那么数字串“110”是 图形(填写“轴对称”、“中心对称”).
11.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成中心对称且也以格点为顶点的三角形共有 个;(不包括△ABC本身)
12.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 .
13.在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是 .
三.解答题
14.如图,试比较正方形和正五边形的异同,请分别写出它们之间的相同点和不同点.(要求:各写3个)
例如:相同点:正方形的对角线相等,正五边形的对角线也相等.
不同点:正方形是中心对称图形,正五边形不是中心对称图形.
15.观察图形,并回答下面的问题:
(1)哪些是轴对称图形?
(2)哪些是中心对称图形?
(3)哪些既是中心对称图形,又是轴对称图形?
(4)哪些既不是中心对称图形,又不是轴对称图形?
16.如图,是5个全等的小正方形组成的图案,请用不同的两种方法分别在两幅图中各添加1个正方形,使整个图案称为中心对称图形.
17.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分分割).
18.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.
19.如图,方格纸中每一个小方格的面积为1个平方单位.
(1)图①中的“OK”可以看成是一个轴对称图形,你能求出图①中“OK”部分的面积吗?
(2)请在图②的方格纸上设计一个中心对称图形,并计算它的面积.
20.如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).
(1)直线y=x﹣经过点C,且与x轴交于点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
答案
一.选择题
C.C.D.D.D.B.C.C.C.
二.填空题
10.轴对称
11.2.
12.③.
13.正三角形.
三.解答题
14.解:比较正方形和正五边形,发现它们的相同点有:①对角线相等;②外角和都是360°;③都是轴对称图形.
不同点有:①正方形是中心对称图形,正五边形不是中心对称图形;②正方形的内角和是360°,正五边形的内角和是540°;③正方形有两条对角线,正五边形有五条对角线.
15.解:(1)①②③是轴对称图形;
(2)①③⑤是中心对称图形;
(3)①③⑥既是中心对称图形,又是轴对称图形;
(4)④⑥既不是中心对称图形,又不是轴对称图形.
16.解:如图所示:
.
17.解:(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB=S四边形DEFC;
(2)如图所示:
(3)如图所示:
18.证明:∵△ABO与△CDO关于O点中心对称,
∴BO=DO,AO=CO,
∵AF=CE,
∴AO﹣AF=CO﹣CE,
∴FO=EO,
在△FOD和△EOB中
,
∴△FOD≌△EOB(SAS),
∴DF=BE.
19.解:(1)“OK”部分的面积为:22;
(2)如图②所示:平行四边形ABCD即为所求,其面积为:3×5=15.
20.解:(1),当y=0时,x=2,
所以E(2,0),
由已知可得:AD=AB=BC=DC=4,AB∥DC,
所以四边形AECD是直角梯形,
所以四边形AECD的面积S=(2﹣1+4)×4÷2=10,
答:四边形AECD的面积是10;
(2)在DC上取一点G,使CG=AE=1,
则S梯形AEGD=S梯形EBCG,易得点G坐标为(4,4),
设直线l的表达式是y=kx+b,
将点E(2,0)代入得:2k+b=0,即b=﹣2k,
将点G(4,4)代入得:4k+b=4,即4k﹣2k=4,
解得k=2,所以b=﹣4,所以y=2x﹣4,
答:直线l的表达式是y=2x﹣4.
一.选择题
1.下列四个图形中,是中心对称图形的是( )
A. B. C. D.
2.下面四个图标中,中心对称图形个数是( )
A.0 B.1个 C.2个 D.3个
3.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
4.下列图形是中心对称图形的是( )
A.等腰三角形 B.直角三角形 C.四边形 D.平行四边形
5.电动伸缩门是依据平行四边形的( )
A.中心对称性 B.轴对称性 C.稳定性 D.不稳定性
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
7.下列图形中:①等边三角形;②矩形;③平行四边形;④菱形;既是中心对称图形又是轴对称图形的有( )个
A.4 B.3 C.2 D.1
8.下列四张扑克牌中,左旋转180°后还是和原来一样的是( )
A. B. C. D.
9.如图将①②③④中的一块涂成阴影能与图中原有阴影部分组成中心对称图形的是( )
A.④ B.③ C.② D.①
二.填空题
10.若数字串“000”和数字串“101”既是轴对称图形,又是中心对称图形,那么数字串“110”是 图形(填写“轴对称”、“中心对称”).
11.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成中心对称且也以格点为顶点的三角形共有 个;(不包括△ABC本身)
12.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 .
13.在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是 .
三.解答题
14.如图,试比较正方形和正五边形的异同,请分别写出它们之间的相同点和不同点.(要求:各写3个)
例如:相同点:正方形的对角线相等,正五边形的对角线也相等.
不同点:正方形是中心对称图形,正五边形不是中心对称图形.
15.观察图形,并回答下面的问题:
(1)哪些是轴对称图形?
(2)哪些是中心对称图形?
(3)哪些既是中心对称图形,又是轴对称图形?
(4)哪些既不是中心对称图形,又不是轴对称图形?
16.如图,是5个全等的小正方形组成的图案,请用不同的两种方法分别在两幅图中各添加1个正方形,使整个图案称为中心对称图形.
17.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分分割).
18.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.
19.如图,方格纸中每一个小方格的面积为1个平方单位.
(1)图①中的“OK”可以看成是一个轴对称图形,你能求出图①中“OK”部分的面积吗?
(2)请在图②的方格纸上设计一个中心对称图形,并计算它的面积.
20.如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).
(1)直线y=x﹣经过点C,且与x轴交于点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
答案
一.选择题
C.C.D.D.D.B.C.C.C.
二.填空题
10.轴对称
11.2.
12.③.
13.正三角形.
三.解答题
14.解:比较正方形和正五边形,发现它们的相同点有:①对角线相等;②外角和都是360°;③都是轴对称图形.
不同点有:①正方形是中心对称图形,正五边形不是中心对称图形;②正方形的内角和是360°,正五边形的内角和是540°;③正方形有两条对角线,正五边形有五条对角线.
15.解:(1)①②③是轴对称图形;
(2)①③⑤是中心对称图形;
(3)①③⑥既是中心对称图形,又是轴对称图形;
(4)④⑥既不是中心对称图形,又不是轴对称图形.
16.解:如图所示:
.
17.解:(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB=S四边形DEFC;
(2)如图所示:
(3)如图所示:
18.证明:∵△ABO与△CDO关于O点中心对称,
∴BO=DO,AO=CO,
∵AF=CE,
∴AO﹣AF=CO﹣CE,
∴FO=EO,
在△FOD和△EOB中
,
∴△FOD≌△EOB(SAS),
∴DF=BE.
19.解:(1)“OK”部分的面积为:22;
(2)如图②所示:平行四边形ABCD即为所求,其面积为:3×5=15.
20.解:(1),当y=0时,x=2,
所以E(2,0),
由已知可得:AD=AB=BC=DC=4,AB∥DC,
所以四边形AECD是直角梯形,
所以四边形AECD的面积S=(2﹣1+4)×4÷2=10,
答:四边形AECD的面积是10;
(2)在DC上取一点G,使CG=AE=1,
则S梯形AEGD=S梯形EBCG,易得点G坐标为(4,4),
设直线l的表达式是y=kx+b,
将点E(2,0)代入得:2k+b=0,即b=﹣2k,
将点G(4,4)代入得:4k+b=4,即4k﹣2k=4,
解得k=2,所以b=﹣4,所以y=2x﹣4,
答:直线l的表达式是y=2x﹣4.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
