八年级数学下册试题 4.5 三角形的中位线-浙教版(含答案)
文档属性
| 名称 | 八年级数学下册试题 4.5 三角形的中位线-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 13:01:54 | ||
图片预览


文档简介
4.5 三角形的中位线
一.选择题
1.如果三角形的两边分别为4和6,那么连接该三角形三边中点所得三角形的周长可能是( )
A.6 B.8 C.10 D.12
2.如图,要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B之间的距离为( )
A.30m B.70m C.105m D.140m
3.已知三角形三边长分别为7cm,8cm,9cm,作三条中位线组成一个新的三角形,同样方法作下去,一共做了五个新的三角形,则这五个新三角形的周长之和为( )
A.46.5cm B.22.5cm C.23.25cm D.以上都不对
4.如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为( )
A.1 B. C. D.
5.如图,直l1∥l2,点A、B固定在直线l2上,点C是直线l1上一动点,若点E、F分别为CA、CB中点,对于下列各值:①线段EF的长;②△CEF的周长;③△CEF的面积;④∠ECF的度数,其中不随点C的移动而改变的是( )
A.①② B.①③ C.②④ D.③④
6.如图,四边形ABCD中,∠ADC=90°,AE=BE,BF=CF,连接EF,AD=3,CD=1,则EF的长为( )
A. B. C. D.
7.如图,△ABC中,D,E分别是AB,AC的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.2.5 B.2 C.1.5 D.1
8.如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC的周长为30,BC=12.则MN的长是( )
A.15 B.9 C.6 D.3
9.顺次连接四边形各边中点所得的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.以上都不对
10.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( )
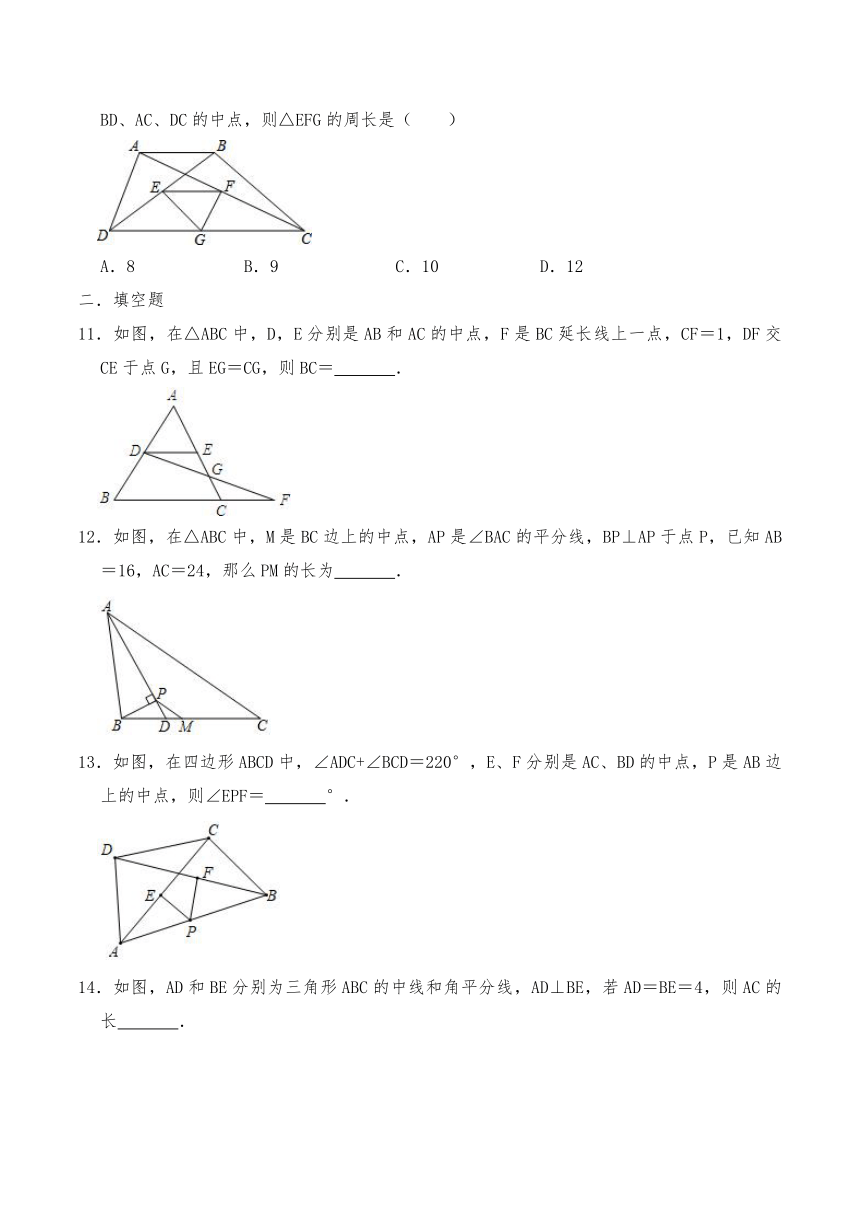
A.8 B.9 C.10 D.12
二.填空题
11.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,CF=1,DF交CE于点G,且EG=CG,则BC= .
12.如图,在△ABC中,M是BC边上的中点,AP是∠BAC的平分线,BP⊥AP于点P,已知AB=16,AC=24,那么PM的长为 .
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF= °.
14.如图,AD和BE分别为三角形ABC的中线和角平分线,AD⊥BE,若AD=BE=4,则AC的长 .
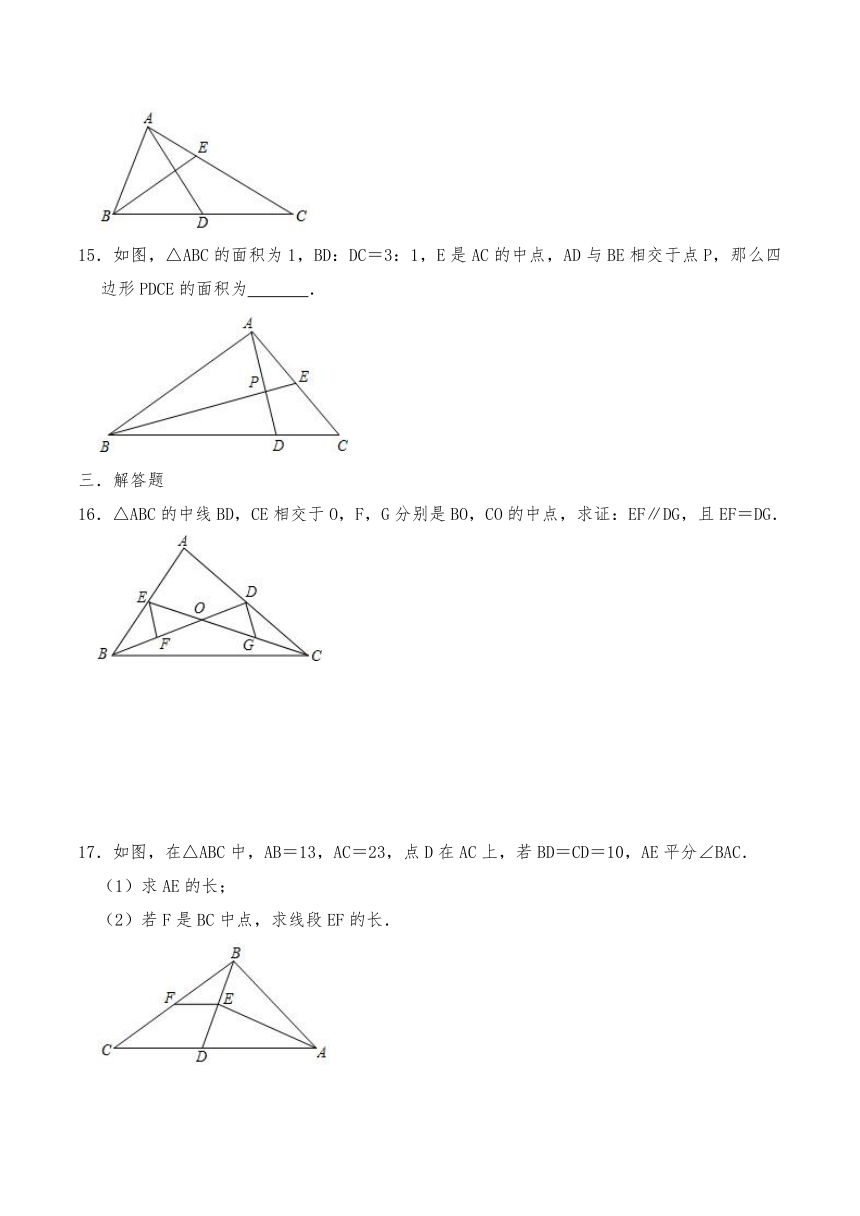
15.如图,△ABC的面积为1,BD:DC=3:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为 .
三.解答题
16.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
17.如图,在△ABC中,AB=13,AC=23,点D在AC上,若BD=CD=10,AE平分∠BAC.
(1)求AE的长;
(2)若F是BC中点,求线段EF的长.
18.如图,四边形ABCD中,AB=CD,E、F分别为AD、BC中点,延长BA、FE交于M,延长FE,CD交于N.求证:∠AME=∠N.
19.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.
答案
一.选择题
B.B.C.C.B.B.C.D.A.B.
二.填空题
11.2.
12.4.
13.40.
14.3.
15..
三.解答题
16.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
17.解:(1)∵AC=23,CD=10,
∴AD=23﹣10=13,
∵AB=13,
∴AB=CD,
∵AE平分∠BAC,
∴DE=BE,AE⊥BD,
∵BD=10,
∴DE=5,
∴AE===12;
(2)∵E是BD的中点,F是BC中点,
∴EF=CD==5.
18.解:连接BD,取BD的中点G,连接EG、FG,
∵DE=EA,DG=GB,
∴EG为△DAB的中位线,
∴EG∥AB,EG=AB,
∴∠GEF=∠AME,
同理,FG∥CD,FG=CD,
∴∠GFE=∠N,
∵AB=CD,
∴EG=FG,
∴∠GEF=∠GFE,
∴∠AME=∠N.
19.证明:取BC中点G,连EG、FG,
∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
一.选择题
1.如果三角形的两边分别为4和6,那么连接该三角形三边中点所得三角形的周长可能是( )
A.6 B.8 C.10 D.12
2.如图,要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B之间的距离为( )
A.30m B.70m C.105m D.140m
3.已知三角形三边长分别为7cm,8cm,9cm,作三条中位线组成一个新的三角形,同样方法作下去,一共做了五个新的三角形,则这五个新三角形的周长之和为( )
A.46.5cm B.22.5cm C.23.25cm D.以上都不对
4.如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为( )
A.1 B. C. D.
5.如图,直l1∥l2,点A、B固定在直线l2上,点C是直线l1上一动点,若点E、F分别为CA、CB中点,对于下列各值:①线段EF的长;②△CEF的周长;③△CEF的面积;④∠ECF的度数,其中不随点C的移动而改变的是( )
A.①② B.①③ C.②④ D.③④
6.如图,四边形ABCD中,∠ADC=90°,AE=BE,BF=CF,连接EF,AD=3,CD=1,则EF的长为( )
A. B. C. D.
7.如图,△ABC中,D,E分别是AB,AC的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.2.5 B.2 C.1.5 D.1
8.如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC的周长为30,BC=12.则MN的长是( )
A.15 B.9 C.6 D.3
9.顺次连接四边形各边中点所得的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.以上都不对
10.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( )
A.8 B.9 C.10 D.12
二.填空题
11.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,CF=1,DF交CE于点G,且EG=CG,则BC= .
12.如图,在△ABC中,M是BC边上的中点,AP是∠BAC的平分线,BP⊥AP于点P,已知AB=16,AC=24,那么PM的长为 .
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF= °.
14.如图,AD和BE分别为三角形ABC的中线和角平分线,AD⊥BE,若AD=BE=4,则AC的长 .
15.如图,△ABC的面积为1,BD:DC=3:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为 .
三.解答题
16.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
17.如图,在△ABC中,AB=13,AC=23,点D在AC上,若BD=CD=10,AE平分∠BAC.
(1)求AE的长;
(2)若F是BC中点,求线段EF的长.
18.如图,四边形ABCD中,AB=CD,E、F分别为AD、BC中点,延长BA、FE交于M,延长FE,CD交于N.求证:∠AME=∠N.
19.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.
答案
一.选择题
B.B.C.C.B.B.C.D.A.B.
二.填空题
11.2.
12.4.
13.40.
14.3.
15..
三.解答题
16.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
17.解:(1)∵AC=23,CD=10,
∴AD=23﹣10=13,
∵AB=13,
∴AB=CD,
∵AE平分∠BAC,
∴DE=BE,AE⊥BD,
∵BD=10,
∴DE=5,
∴AE===12;
(2)∵E是BD的中点,F是BC中点,
∴EF=CD==5.
18.解:连接BD,取BD的中点G,连接EG、FG,
∵DE=EA,DG=GB,
∴EG为△DAB的中位线,
∴EG∥AB,EG=AB,
∴∠GEF=∠AME,
同理,FG∥CD,FG=CD,
∴∠GFE=∠N,
∵AB=CD,
∴EG=FG,
∴∠GEF=∠GFE,
∴∠AME=∠N.
19.证明:取BC中点G,连EG、FG,
∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
