浙教版八年级数学下册试题 5.3 正方形(含答案)
文档属性
| 名称 | 浙教版八年级数学下册试题 5.3 正方形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 13:17:34 | ||
图片预览



文档简介
5.3 正方形
一.选择题
1.正方形具有而菱形不具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线平分一组对角 D.对角线互相垂直
2.如图,在边长为2的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于点E,MF⊥CD于点F,连接EF,则EF的最小值为( )
A.1 B. C. D.
3.下列说法正确的是( )
A.对角线互相垂直平分的四边形的正方形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相平分的四边形是平行四边形
4.一个正方形的对角线长为2cm,则它的面积是( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
5.如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是( )
A.∠DAB=90°且AD=BC B.AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D.AC⊥BD且AO=BO=CO=DO
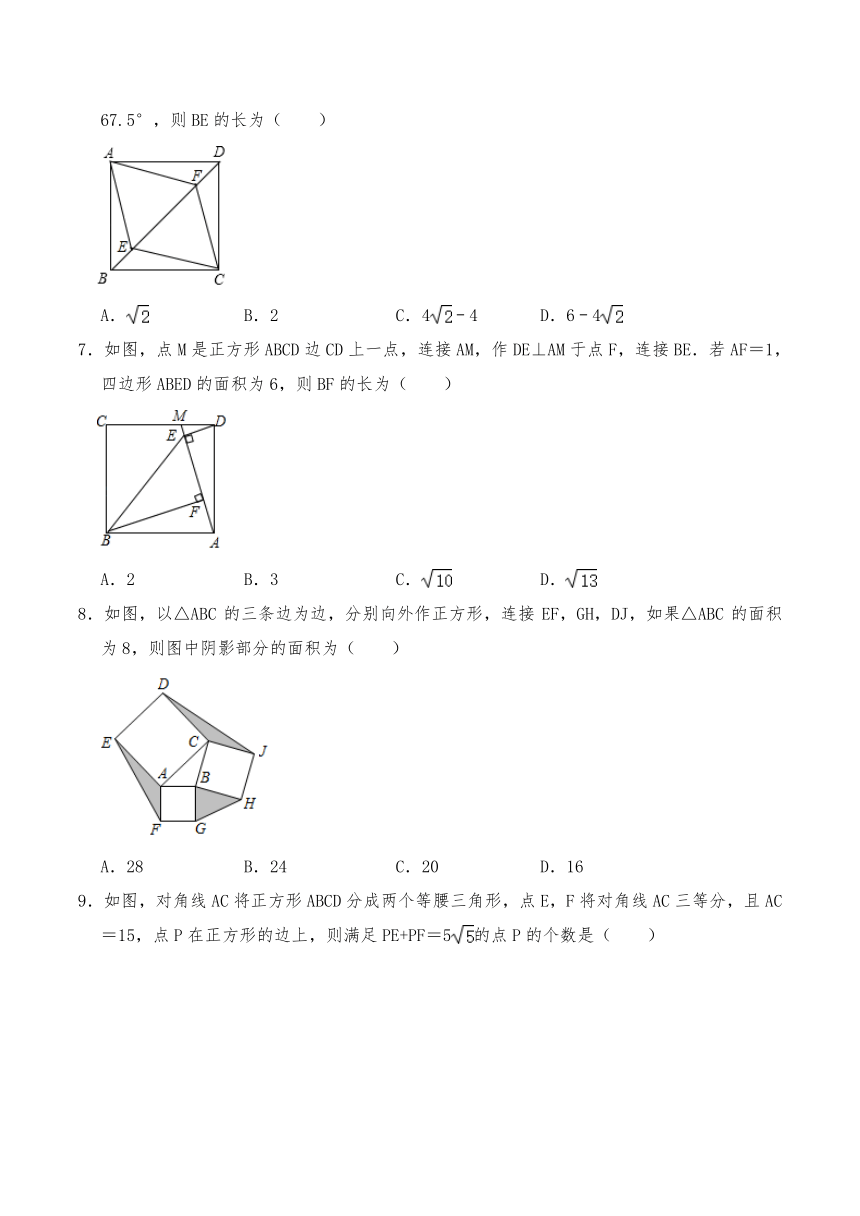
6.如图,正方形ABCD的边长为4,点E,F在对角线BD上,四边形AECF是菱形,且∠DAE=67.5°,则BE的长为( )
A. B.2 C.4﹣4 D.6﹣4
7.如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点F,连接BE.若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2 B.3 C. D.
8.如图,以△ABC的三条边为边,分别向外作正方形,连接EF,GH,DJ,如果△ABC的面积为8,则图中阴影部分的面积为( )
A.28 B.24 C.20 D.16
9.如图,对角线AC将正方形ABCD分成两个等腰三角形,点E,F将对角线AC三等分,且AC=15,点P在正方形的边上,则满足PE+PF=5的点P的个数是( )
A.0 B.4 C.8 D.16
10.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④EF的最小值为2.其中正确结论的序号为( )
A.①③④ B.①④ C.②③④ D.①②④
二.填空题
11.如图,在正方形ABCD中,延长BC至E,使CE=CA,则∠E的度数是 .
12.已知正方形ABCD,以∠BAE为顶角,边AB为腰作等腰△ABE,连接DE,则∠DEB= .
13.如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm.
14.如图,以直角三角形ABC的斜边BC为边在三角形ABC的同侧作正方形BCEF,设正方形的中心为O,连结AO,如果AB=4,AO=6,则AC= .
15.如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为 .
16.如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是 .
三.解答题
17.如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
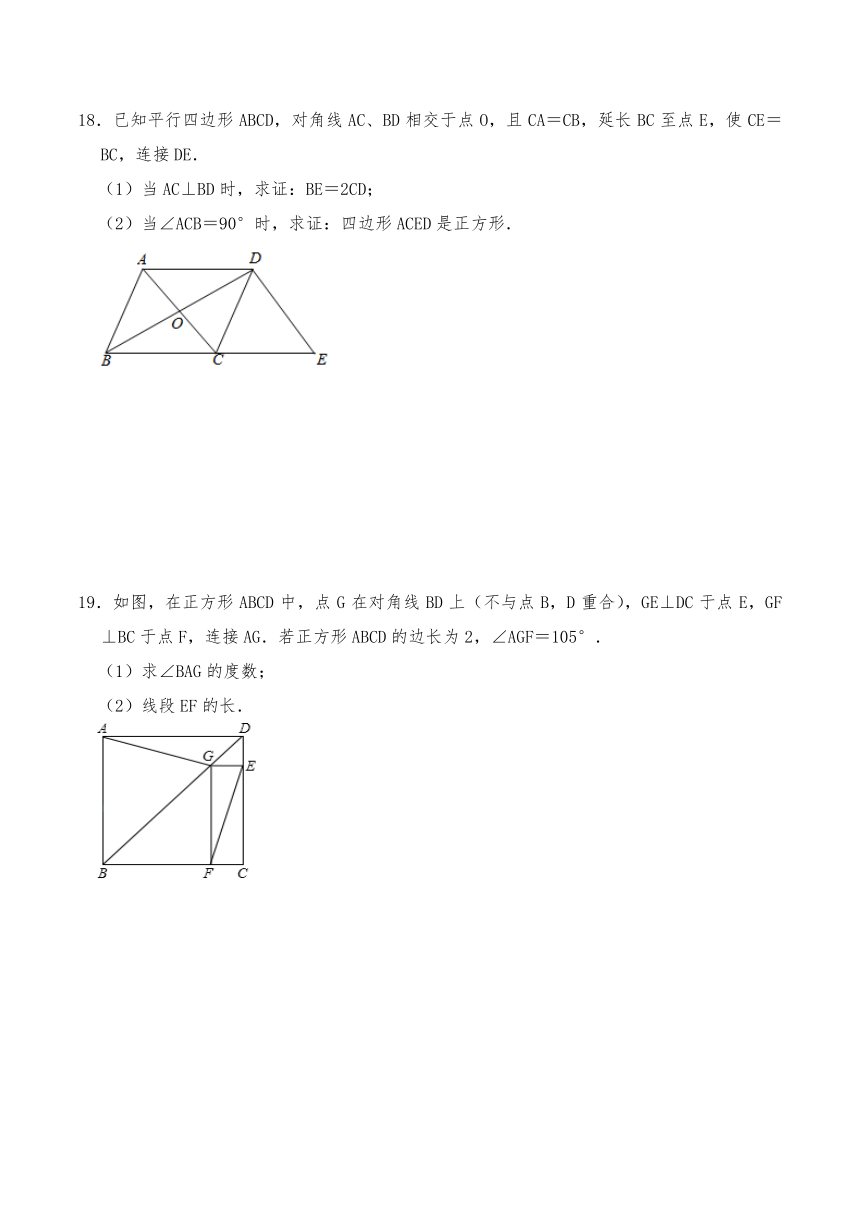
18.已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
19.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.若正方形ABCD的边长为2,∠AGF=105°.
(1)求∠BAG的度数;
(2)线段EF的长.
20.正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上
①若AB=BE,求∠DAE度数;
②求证:CE=EF
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.
21.如图,平行四边形ABCD中,AD=9cm,CD=3cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
22.如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
23.如图,正方形ABCD边长为4,点O在对角线DB上运动(不与点B,D重合),连接OA,作OP⊥OA,交直线BC于点P.
(1)判断线段OA,OP的数量关系,并说明理由.
(2)当OD=时,求CP的长.
(3)设线段DO,OP,PC,CD围成的图形面积为S1,△AOD的面积为S2,求S1﹣S2的最值.
答案
一.选择题
B.D.D.A.D.C.B.B.B.D.
二.填空题
11.22.5°
12.135°或45°.
13.1或2.
14.16
15.3s或7s
16.①③⑤.
三.解答题
17.(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
AC⊥BD.
∵BE=DF,
∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,
∴AO=AC,BO=BD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB==3,
∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE===3.
∵四边形AECF是菱形,
∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.
∴四边形AECF的周长是12.
18.(1)证明:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形.
∴BC=CD.
又∵CE=BC,
∴BE=2BC,
∴BE=2CD;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BE,
又∵CE=BC,
∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形.
∵∠ACB=90°,
∴平行四边形ACED是矩形,
又∵CA=CB,
∴CA=CE,
∴矩形ACED是正方形.
19.解:(1)∵四边形ABCD是正方形,
∴∠DBC=∠ABG=45°,AB=BC=CD=2,
∵GF⊥BC,
∴∠GBF=45°=∠BGF,
∵∠AGF=105°,
∴∠AGB=60°,
∵∠AGB+∠BAG+∠ABG=180°,
∴∠BAG=180°﹣45°﹣60°=75°;
(2)如图,连接CG,过点A作AH⊥BD于点H,
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴EF=GC,
∴AG=EF,
∵AB=2,∠ABH=45°,AH⊥BG,
∴BH=AH=,
∵∠AGB=60°,AH⊥BG,AH=,
∴HG===,AG=2HG=,
∴EF=.
20.解:(1)①∵ABCD为正方形,
∴∠ABE=45°.
又∵AB=BE,
∴∠BAE=×(180°﹣45°)=67.5°.
∴∠DAE=90°﹣67.5°=22.5°
②证明:∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
(2)如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵CE=EF,
∴N是CF的中点.
∵BC=2BF,
∴=.
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED=DM=CN=.
如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=3,
∴CN=,
∴EN=BN=,
∴DE=.
综上所述,ED的长为或
21.解:(1)∵四边形ABCD是平行四边形,
∴AB=CD=3cm.
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=AB sin∠B=3×=3(cm);
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=6﹣t,
∴AN2=32+(6﹣t)2,
∴32+(6﹣t)2=t2,
解得t=.
故当t为时,四边形AMCN为菱形;
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC﹣BE﹣CN=9﹣3﹣t=6﹣t,
∴QM=AM﹣AQ=|t﹣(6﹣t)|=|2t﹣6|(注:分点Q在点M的左右两种情况),
∵QN=AE=3,
∴|2t﹣6|=3,
解得t=4.5或t=1.5.
故当t为4.5或1.5秒时,四边形MPNQ为正方形.
22.证明:(1)连接GC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,
∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,
∴∠BCG=∠GFC,
∴GC=GF,
∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,
∴AF2=AB2+BF2=AG2+GF2,
∴GF2=58,
∵∠DBC=45°,GH⊥BC,
∴BH=GH,BG=GH,
∵GF2=GH2+FH2,
∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),
∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,
∴∠EAF=45°,
∵AE=AF,AB=AD,
∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,
∴CF=CE,
∵BF=BN,∠ABC=90°,
∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,
∴AN=NF=BF,
∵AB=BC,
∴BN+AN=BF+FC,
∴FC=BF,
∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
23.解:(1)OA=OP,理由是:
如图1,过O作OG⊥AB于G,过O作OH⊥BC于H,
∵四边形ABCD是正方形,
∴∠ABO=∠CBO,AB=BC,
∴OG=OH,
∵∠OGB=∠GBH=∠BHO=90°,
∴四边形OGBH是正方形,
∴BG=BH,∠GOH=90°,
∵∠AOP=∠GOH=90°,
∴∠AOG=∠POH,
∴△AGO≌△PHO(ASA),
∴OA=OP;
(2)如图2,过O作OQ⊥CD于Q,过O作OH⊥BC于H,连接OC,
∴∠OQD=90°,
∵∠ODQ=45°,
∴△ODQ是等腰直角三角形,
∵OD=,
∴OQ=DQ=1,
∵AD=CD,∠ADO=∠CDO,OD=OD,
∴△ADO≌△CDO(SAS),
∴AO=OC=OP,
∵OH⊥PC,
∴PH=CH=OQ=1,
∴PC=2;
(3)如图3,连接OC,过O作OG⊥BC于G,OH⊥CD于H,
设OH=x,则DH=x,CH=OG=4﹣x,PC=2x,
由(2)知:△AOD≌△COD,
∴S△AOD=S△COD,
∴S1﹣S2=S1﹣S△COD=S△POC===﹣x2+4x=﹣(x﹣2)2+4,
当x=2时,S1﹣S2有最大值是4,
当x=0和x=4时,S1﹣S2有最小值是0,
∵点O在对角线DB上运动(不与点B,D重合),
∴0<x<4,
∴S1﹣S2没有最小值
综上,S1﹣S2有最大值是4.
一.选择题
1.正方形具有而菱形不具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线平分一组对角 D.对角线互相垂直
2.如图,在边长为2的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于点E,MF⊥CD于点F,连接EF,则EF的最小值为( )
A.1 B. C. D.
3.下列说法正确的是( )
A.对角线互相垂直平分的四边形的正方形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相平分的四边形是平行四边形
4.一个正方形的对角线长为2cm,则它的面积是( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
5.如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是( )
A.∠DAB=90°且AD=BC B.AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D.AC⊥BD且AO=BO=CO=DO
6.如图,正方形ABCD的边长为4,点E,F在对角线BD上,四边形AECF是菱形,且∠DAE=67.5°,则BE的长为( )
A. B.2 C.4﹣4 D.6﹣4
7.如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点F,连接BE.若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2 B.3 C. D.
8.如图,以△ABC的三条边为边,分别向外作正方形,连接EF,GH,DJ,如果△ABC的面积为8,则图中阴影部分的面积为( )
A.28 B.24 C.20 D.16
9.如图,对角线AC将正方形ABCD分成两个等腰三角形,点E,F将对角线AC三等分,且AC=15,点P在正方形的边上,则满足PE+PF=5的点P的个数是( )
A.0 B.4 C.8 D.16
10.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④EF的最小值为2.其中正确结论的序号为( )
A.①③④ B.①④ C.②③④ D.①②④
二.填空题
11.如图,在正方形ABCD中,延长BC至E,使CE=CA,则∠E的度数是 .
12.已知正方形ABCD,以∠BAE为顶角,边AB为腰作等腰△ABE,连接DE,则∠DEB= .
13.如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm.
14.如图,以直角三角形ABC的斜边BC为边在三角形ABC的同侧作正方形BCEF,设正方形的中心为O,连结AO,如果AB=4,AO=6,则AC= .
15.如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为 .
16.如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是 .
三.解答题
17.如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
18.已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
19.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.若正方形ABCD的边长为2,∠AGF=105°.
(1)求∠BAG的度数;
(2)线段EF的长.
20.正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上
①若AB=BE,求∠DAE度数;
②求证:CE=EF
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.
21.如图,平行四边形ABCD中,AD=9cm,CD=3cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
22.如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
23.如图,正方形ABCD边长为4,点O在对角线DB上运动(不与点B,D重合),连接OA,作OP⊥OA,交直线BC于点P.
(1)判断线段OA,OP的数量关系,并说明理由.
(2)当OD=时,求CP的长.
(3)设线段DO,OP,PC,CD围成的图形面积为S1,△AOD的面积为S2,求S1﹣S2的最值.
答案
一.选择题
B.D.D.A.D.C.B.B.B.D.
二.填空题
11.22.5°
12.135°或45°.
13.1或2.
14.16
15.3s或7s
16.①③⑤.
三.解答题
17.(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
AC⊥BD.
∵BE=DF,
∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,
∴AO=AC,BO=BD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB==3,
∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE===3.
∵四边形AECF是菱形,
∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.
∴四边形AECF的周长是12.
18.(1)证明:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形.
∴BC=CD.
又∵CE=BC,
∴BE=2BC,
∴BE=2CD;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BE,
又∵CE=BC,
∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形.
∵∠ACB=90°,
∴平行四边形ACED是矩形,
又∵CA=CB,
∴CA=CE,
∴矩形ACED是正方形.
19.解:(1)∵四边形ABCD是正方形,
∴∠DBC=∠ABG=45°,AB=BC=CD=2,
∵GF⊥BC,
∴∠GBF=45°=∠BGF,
∵∠AGF=105°,
∴∠AGB=60°,
∵∠AGB+∠BAG+∠ABG=180°,
∴∠BAG=180°﹣45°﹣60°=75°;
(2)如图,连接CG,过点A作AH⊥BD于点H,
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴EF=GC,
∴AG=EF,
∵AB=2,∠ABH=45°,AH⊥BG,
∴BH=AH=,
∵∠AGB=60°,AH⊥BG,AH=,
∴HG===,AG=2HG=,
∴EF=.
20.解:(1)①∵ABCD为正方形,
∴∠ABE=45°.
又∵AB=BE,
∴∠BAE=×(180°﹣45°)=67.5°.
∴∠DAE=90°﹣67.5°=22.5°
②证明:∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
(2)如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵CE=EF,
∴N是CF的中点.
∵BC=2BF,
∴=.
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED=DM=CN=.
如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=3,
∴CN=,
∴EN=BN=,
∴DE=.
综上所述,ED的长为或
21.解:(1)∵四边形ABCD是平行四边形,
∴AB=CD=3cm.
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=AB sin∠B=3×=3(cm);
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=6﹣t,
∴AN2=32+(6﹣t)2,
∴32+(6﹣t)2=t2,
解得t=.
故当t为时,四边形AMCN为菱形;
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC﹣BE﹣CN=9﹣3﹣t=6﹣t,
∴QM=AM﹣AQ=|t﹣(6﹣t)|=|2t﹣6|(注:分点Q在点M的左右两种情况),
∵QN=AE=3,
∴|2t﹣6|=3,
解得t=4.5或t=1.5.
故当t为4.5或1.5秒时,四边形MPNQ为正方形.
22.证明:(1)连接GC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,
∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,
∴∠BCG=∠GFC,
∴GC=GF,
∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,
∴AF2=AB2+BF2=AG2+GF2,
∴GF2=58,
∵∠DBC=45°,GH⊥BC,
∴BH=GH,BG=GH,
∵GF2=GH2+FH2,
∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),
∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,
∴∠EAF=45°,
∵AE=AF,AB=AD,
∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,
∴CF=CE,
∵BF=BN,∠ABC=90°,
∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,
∴AN=NF=BF,
∵AB=BC,
∴BN+AN=BF+FC,
∴FC=BF,
∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
23.解:(1)OA=OP,理由是:
如图1,过O作OG⊥AB于G,过O作OH⊥BC于H,
∵四边形ABCD是正方形,
∴∠ABO=∠CBO,AB=BC,
∴OG=OH,
∵∠OGB=∠GBH=∠BHO=90°,
∴四边形OGBH是正方形,
∴BG=BH,∠GOH=90°,
∵∠AOP=∠GOH=90°,
∴∠AOG=∠POH,
∴△AGO≌△PHO(ASA),
∴OA=OP;
(2)如图2,过O作OQ⊥CD于Q,过O作OH⊥BC于H,连接OC,
∴∠OQD=90°,
∵∠ODQ=45°,
∴△ODQ是等腰直角三角形,
∵OD=,
∴OQ=DQ=1,
∵AD=CD,∠ADO=∠CDO,OD=OD,
∴△ADO≌△CDO(SAS),
∴AO=OC=OP,
∵OH⊥PC,
∴PH=CH=OQ=1,
∴PC=2;
(3)如图3,连接OC,过O作OG⊥BC于G,OH⊥CD于H,
设OH=x,则DH=x,CH=OG=4﹣x,PC=2x,
由(2)知:△AOD≌△COD,
∴S△AOD=S△COD,
∴S1﹣S2=S1﹣S△COD=S△POC===﹣x2+4x=﹣(x﹣2)2+4,
当x=2时,S1﹣S2有最大值是4,
当x=0和x=4时,S1﹣S2有最小值是0,
∵点O在对角线DB上运动(不与点B,D重合),
∴0<x<4,
∴S1﹣S2没有最小值
综上,S1﹣S2有最大值是4.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
