2.1有理数的加法(浙江省温州市平阳县)

课件23张PPT。2.1有理数的加法（一） 温州实验中学 张章一 教材分析自然数、分数有理数加法是其中最基础的运算数学的抽象内容生产生活实际数轴的运用数形运算发生了变化二 教学目标知识与技能了解法则的产生过程根据法则计算方法与过程 观察、分析、抽象概括情感与态度联系实际学习兴趣探究与合作经历 用数轴来表示有理数的加法有理数的加法法则异号两数相加四 学情分析三 教学重难点形象思维抽象思维概念描述问题五 教法学法情景教学法六 教学过程 1、创设情境，探索新知 2、练习反馈，巩固新知 3、尝试应用，拓展新知 4、归纳小结，布置作业自主探索
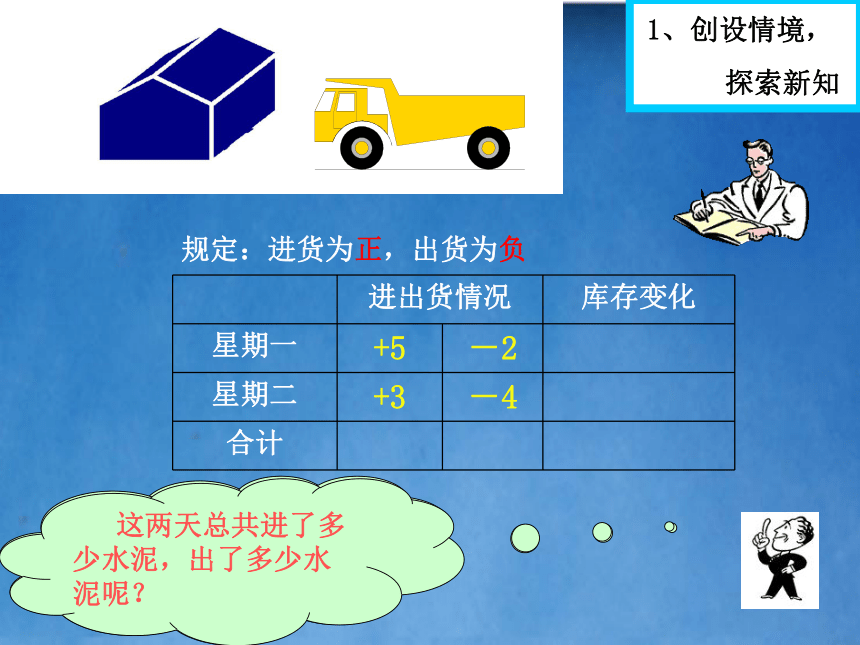
互相交流 你能向我汇报一下星期一和星期二的进出货情况吗？ 这两天总共进了多少水泥，出了多少水泥呢？ 1、创设情境，
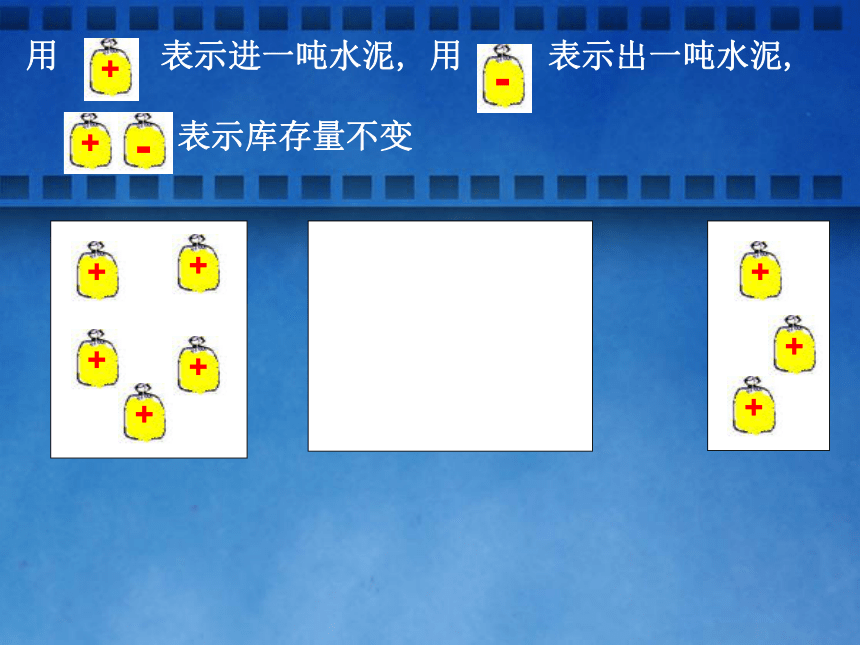
探索新知规定：进货为正，出货为负用 表示进一吨水泥, 用 表示出一吨水泥,

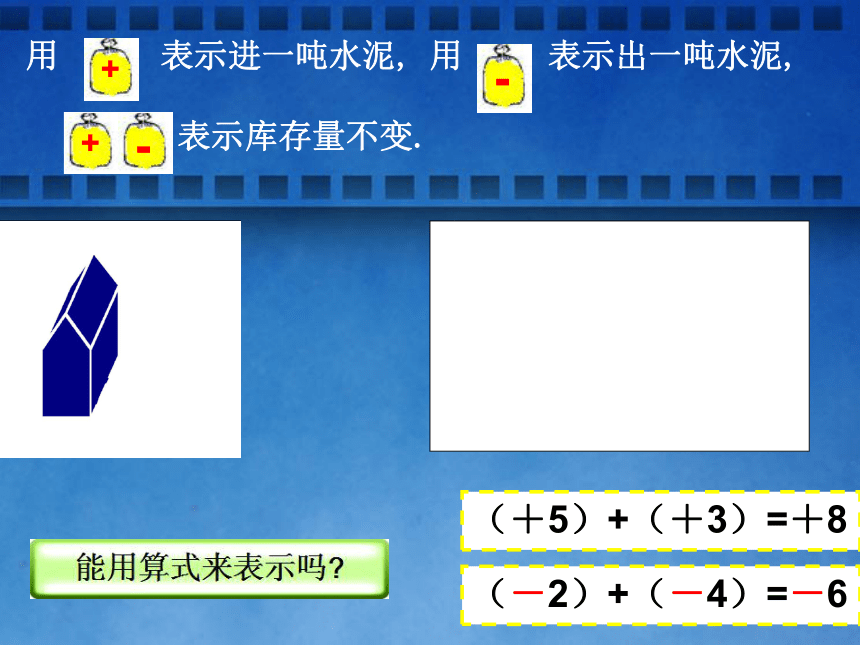
表示库存量不变用 表示进一吨水泥, 用 表示出一吨水泥,

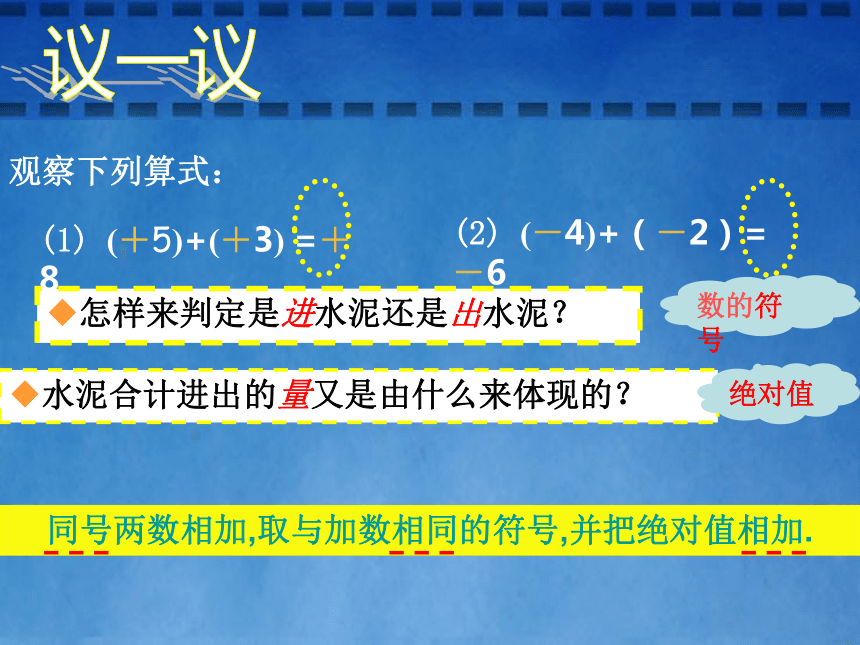
表示库存量不变.（＋5）+（＋3）=＋8（－2）+（－4）=－6 同号两数相加,取与加数相同的符号,并把绝对值相加.(1) (＋5)+(＋3) =＋8观察下列算式：(2) (－4)+（－2）=－6 怎样来判定是进水泥还是出水泥？ 水泥合计进出的量又是由什么来体现的？ 议一议数的符号绝对值 那星期一仓库的水泥库存是增加了还是减少了？星期二呢？
算式：（＋5）+（－2）=＋3星期一 异号两数相加,取与绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.浙教版初中数学七年级上 有理数的加法 算式：（＋3）+（－4）=－1算式：（＋5）+（－2）=＋3 和的符号与绝对值怎么决定呢？确定下列各题中和的符号，并说明理由.
（1）（＋5）+（＋7）；
（2）（－10）+（－3）；

（3）（＋6）+（－5）； 小试牛刀（1）仓库在周三上午进了3吨水泥，下午出了3吨水泥，你能列算式来表示这一天的库存变化吗？(1) (＋3)+(－3) =0（2）周四上午出了4吨水泥，下午没进也没出，同样你能列算式来表示这一天的库存变化吗？(2) (－4)+ 0 = －4帮我算一算！有理数的加法 互为相反数的两个数相加得零；一个数同零相加仍得这个数. 同号两数相加，取与加数相同的符号，并把绝对值相加.
异号两数相加，取与绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得零；一个数同零相加仍得这个数.
一起说一说 计算下列各式：
(1)（－11）+（－9） (2)（－3.5）+（＋7）
(3)（－1.08）+0 (4)解:原式=－（11+9）
=－20（同号两数相加）（异号两数相加）解:原式=－（7-3.5）
=－3.5（一个数同0相加）（互为相反数得两数相加）解:原式=－1.08解:原式=0一起算一算 2、练习反馈，巩固新知过关斩将 (＋7.3)+(＋3.7)
(－42)+(＋17)
0+(－39.98)

老板派了甲乙丙丁四辆车向四个地方运送水泥. 如果规定向东为正，向西为负，你能算出它们最后停在哪里吗？过关斩将甲：从仓库出发，先向东行驶2千米，再向东行驶3千米；
乙：从仓库出发，先向东行驶2千米，再向西行驶3千米；
丙：从仓库出发，先向西行驶3千米，再向西行驶2千米；
丁：从仓库出发，先向西行驶5千米，再向东行驶4千米. 3、尝试应用， 拓展新知我们规定以仓库为原点，向东为正方向，向西为负方向. 甲：从仓库出发，先向东行驶2千米，再向东行驶3千米. 乙：从仓库出发，先向东行驶2千米，再向西行驶3千米.数轴可以表示有理数的加法你能利用数轴上求得丙与丁最后停在哪里吗？
过关斩将三 丙：从仓库出发，先向西行驶3千米，再向西行驶2千米；
丁：从仓库出发，先向西行驶5千米，再向东行驶4千米. 1.你能根据
编一道应用题吗？能力大挑战算式：－45＋30＝－15今天你有什么收获?分层作业：作业本，课后2、3、4必做6选做蓦然回首 4、归纳小结，布置作业