黄金分割(浙江省温州市平阳县)
图片预览







文档简介
课件27张PPT。地位作用:
教学分析 “黄金分割”是义务教育课程标准实验教科书 — 北师大教材八年级下册第四章第二节课的内容。是 在学习了线段的比、成比例线段的基础上,对所学 知识在现实生活中的应用。是古希腊人在探求美感
产生的数字化规律,体现了人类对美的追求。在建
筑、艺术上都有较多的体现。
教学分析教学目标知识技能目标:
(1)通过建筑艺术上的实例了解黄金分割,体会其中的文化价值。
(2)在应用中进一步理解线段的比、成比例线段等相关内容,在实际操作、思考、交流等过程中增强学生的实践意识和自信心。过程方法目标:
(1)经过收集素材加强对线段比例关系的认识.
(2)在现实情境中了解黄金分割的文化价值,进而由实际问题
去探索黄金分割的作图方法,让学生感受到黄金分割在实
际生活中的实用性。情感态度目标:
(1)从学生乐于接受的现实背景中学习黄金分割,认识到数学上解决实际问题和进行交流的重要工具。
(2)通过对黄金分割的理解和掌握,明确黄金分割的作图方法,体会数形结合的思想。
(3)通过分组讨论学习,体会在解决实际问题的过程与他人合作的重要性,从而培养学生的团结协作精神。教学分析教学重点:
黄金分割的定义,以及简单的应用。
教学难点:
黄金比的理解及黄金分割的作图。
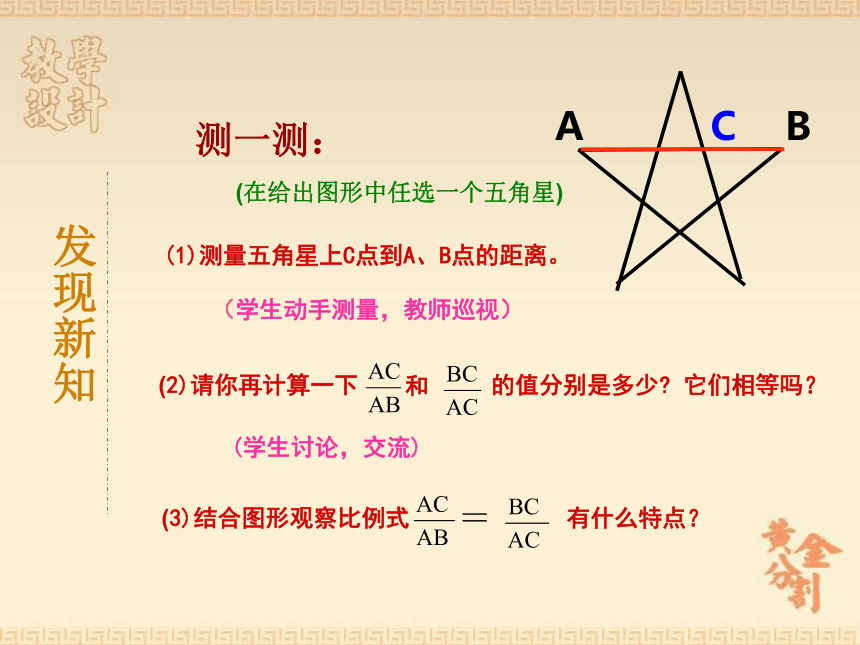
教学重难点教学分析 学法 指导1、采用教师引导,学生自主探索和小组合作相结合的学习方式。2、利用多媒体和实物投影等教学设备辅助教学,充分调动学生的积极性,创设和谐、轻松的学习氛围。 学生通过动手、动口、动脑等活动,主动探索,发现问题,小组之间互相合作,取长补短。养成自主学习和合作学习相结合的良好习惯。教学方法和手段作 图建筑 艺术教学分析教学流程图:发现新知应用新知再探新知生活拓展发现新知请将卡通人物放在图片中你认为最合适的位置,使图片看起来最美。摆一摆:发现新知测一测: (1)测量五角星上C点到A、B点的距离。
(学生动手测量,教师巡视)
(在给出图形中任选一个五角星)发现新知概 念:如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,那么称线段 AB 被点 C 黄金分割(golden section),点 C 叫做线段 AB 的黄金分割点,AC 与 AB 的比叫做黄金比.问:黄金比是多少?应用新知应用新知巴台农神庙(Parthenom Temple) 如果用图中的虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,应用新知FDCAEB1.点E是AB的黄金分割点吗?2.矩形ABCD的宽与长的比是
黄金比吗?宽与长的比等于黄金比的矩形也成为黄金矩形黄金分割点的作法再探新知A、B层(基础一般)的学生分层教学再探新知C层(基础较好)的学生黄金分割点的作法【生1】可利用在数轴上表示一个实数的方法,构
造Rt△。
(积极思考探索之后,让学生尝试根据课本98页的步骤操作,交流)
分层教学再探新知想一想:(1)如果设AB=1,那么(2)点C是线段AB的黄金分割点吗? ? ? ? ?BD=AD=AC=BC=再探新知异 曲 同 工如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH。点H就是AB的黄金分割点。你能说说这种作法的道理吗?EF生活拓展黄金分割在生活中的应用我来说说生活拓展人与黄金分割 人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618)。这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.生活拓展 东方明珠塔,塔高462.85米。设计师将在295米处设计了一个上球体,使平直单调的塔身变得丰富多彩,非常协调、美观。黄金建筑设计:上海-----东方明珠生活拓展生活拓展阅读材料 黄金分割的历史
黄金分割是古希腊哲学家毕达哥拉斯发现。一天,毕达哥拉斯从一家铁匠铺路过,被铺子中那有节奏的叮叮当当的打铁声所吸引,便站在那里仔细聆听,似乎这声音中隐匿着什么秘密。他走进作坊,拿出一把尺量了一下铁锤和铁砧的尺寸,发现它们之间存在着一种十分和谐的关系。回到家里,毕达哥拉斯拿出一根线,想将它分为两段。怎样分才最好呢?经过反复比较,他最后确定1:0.618的比例截断最优美。后来,意大利著名科学家、艺术家达·芬奇给这个比例冠以“黄金”二字的美名。历史上最早在书中使用“黄金分割”这个名称的是欧姆(Martin Ohm,1792-1872).19世纪以后“黄金分割”的说法逐渐流行起来。
有意思的是,无论什么物体、图形,只要它各部分的关系与这种分割法相符,这类物体、图形就能给人最悦目、最美的印象。人体各部分之间的比例也符合这一规律。因此,艺术家们在创作艺术人体时,都以黄金分割为标准进行创作。如古希腊神话中的太阳神中的太阳神阿波罗、女神维纳斯的体型。作为建筑艺术,也遵循着这一规律。文艺复兴时的西方艺术家、艺术理论家把黄金分割作为艺术建筑必须遵循的规律。古希腊的巴台农神庙严整的大理石柱廓,就是根据黄金分割律分割整个神庙的,因此看上去显得威武、壮观,成为繁荣和美德的象征(书P99页)。欧洲中世纪的物理学家和天文学家开普勒(J.Kepler1571—1630),曾经说过:“几何学里有二个宝库:一个是毕达哥拉斯定理(我们称为“勾股定理”);另外一个就是黄金分割。前者好比黄金,后者堪称珠玉。” 归 纳 小 结 :今天的学习你有何收获和体会!(1)作业本 习题4.3 第1题。(必做题)
(2)利用“黄金分割”的作法画一个“黄金五角星”。
(C层学生必做;A、B层学生选做)作 业:设计说明: 本节课在了解黄金分割后,以积累数学活
动经验来立意,定位在丰富对线段的比、成
比例线段有关数学知识的认识上,从生活中
经常碰到的问题,如何摆放引入,扩展对黄
金分割的认识,欣赏并挖掘生活中存在黄金
分割知识,重点放在了解黄金分割,体会其
中的文化价值上。谢 谢 大 家!发现新知 《黄金分割》学习资料
学习小组名单: 1、测量五角星上C点到A、B点的距离。
AC=
AB=
BC=
2、请你再计算一下和的值分别是多少,它们相等吗?= ,= ,
教学分析 “黄金分割”是义务教育课程标准实验教科书 — 北师大教材八年级下册第四章第二节课的内容。是 在学习了线段的比、成比例线段的基础上,对所学 知识在现实生活中的应用。是古希腊人在探求美感
产生的数字化规律,体现了人类对美的追求。在建
筑、艺术上都有较多的体现。
教学分析教学目标知识技能目标:
(1)通过建筑艺术上的实例了解黄金分割,体会其中的文化价值。
(2)在应用中进一步理解线段的比、成比例线段等相关内容,在实际操作、思考、交流等过程中增强学生的实践意识和自信心。过程方法目标:
(1)经过收集素材加强对线段比例关系的认识.
(2)在现实情境中了解黄金分割的文化价值,进而由实际问题
去探索黄金分割的作图方法,让学生感受到黄金分割在实
际生活中的实用性。情感态度目标:
(1)从学生乐于接受的现实背景中学习黄金分割,认识到数学上解决实际问题和进行交流的重要工具。
(2)通过对黄金分割的理解和掌握,明确黄金分割的作图方法,体会数形结合的思想。
(3)通过分组讨论学习,体会在解决实际问题的过程与他人合作的重要性,从而培养学生的团结协作精神。教学分析教学重点:
黄金分割的定义,以及简单的应用。
教学难点:
黄金比的理解及黄金分割的作图。
教学重难点教学分析 学法 指导1、采用教师引导,学生自主探索和小组合作相结合的学习方式。2、利用多媒体和实物投影等教学设备辅助教学,充分调动学生的积极性,创设和谐、轻松的学习氛围。 学生通过动手、动口、动脑等活动,主动探索,发现问题,小组之间互相合作,取长补短。养成自主学习和合作学习相结合的良好习惯。教学方法和手段作 图建筑 艺术教学分析教学流程图:发现新知应用新知再探新知生活拓展发现新知请将卡通人物放在图片中你认为最合适的位置,使图片看起来最美。摆一摆:发现新知测一测: (1)测量五角星上C点到A、B点的距离。
(学生动手测量,教师巡视)
(在给出图形中任选一个五角星)发现新知概 念:如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,那么称线段 AB 被点 C 黄金分割(golden section),点 C 叫做线段 AB 的黄金分割点,AC 与 AB 的比叫做黄金比.问:黄金比是多少?应用新知应用新知巴台农神庙(Parthenom Temple) 如果用图中的虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,应用新知FDCAEB1.点E是AB的黄金分割点吗?2.矩形ABCD的宽与长的比是
黄金比吗?宽与长的比等于黄金比的矩形也成为黄金矩形黄金分割点的作法再探新知A、B层(基础一般)的学生分层教学再探新知C层(基础较好)的学生黄金分割点的作法【生1】可利用在数轴上表示一个实数的方法,构
造Rt△。
(积极思考探索之后,让学生尝试根据课本98页的步骤操作,交流)
分层教学再探新知想一想:(1)如果设AB=1,那么(2)点C是线段AB的黄金分割点吗? ? ? ? ?BD=AD=AC=BC=再探新知异 曲 同 工如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH。点H就是AB的黄金分割点。你能说说这种作法的道理吗?EF生活拓展黄金分割在生活中的应用我来说说生活拓展人与黄金分割 人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618)。这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.生活拓展 东方明珠塔,塔高462.85米。设计师将在295米处设计了一个上球体,使平直单调的塔身变得丰富多彩,非常协调、美观。黄金建筑设计:上海-----东方明珠生活拓展生活拓展阅读材料 黄金分割的历史
黄金分割是古希腊哲学家毕达哥拉斯发现。一天,毕达哥拉斯从一家铁匠铺路过,被铺子中那有节奏的叮叮当当的打铁声所吸引,便站在那里仔细聆听,似乎这声音中隐匿着什么秘密。他走进作坊,拿出一把尺量了一下铁锤和铁砧的尺寸,发现它们之间存在着一种十分和谐的关系。回到家里,毕达哥拉斯拿出一根线,想将它分为两段。怎样分才最好呢?经过反复比较,他最后确定1:0.618的比例截断最优美。后来,意大利著名科学家、艺术家达·芬奇给这个比例冠以“黄金”二字的美名。历史上最早在书中使用“黄金分割”这个名称的是欧姆(Martin Ohm,1792-1872).19世纪以后“黄金分割”的说法逐渐流行起来。
有意思的是,无论什么物体、图形,只要它各部分的关系与这种分割法相符,这类物体、图形就能给人最悦目、最美的印象。人体各部分之间的比例也符合这一规律。因此,艺术家们在创作艺术人体时,都以黄金分割为标准进行创作。如古希腊神话中的太阳神中的太阳神阿波罗、女神维纳斯的体型。作为建筑艺术,也遵循着这一规律。文艺复兴时的西方艺术家、艺术理论家把黄金分割作为艺术建筑必须遵循的规律。古希腊的巴台农神庙严整的大理石柱廓,就是根据黄金分割律分割整个神庙的,因此看上去显得威武、壮观,成为繁荣和美德的象征(书P99页)。欧洲中世纪的物理学家和天文学家开普勒(J.Kepler1571—1630),曾经说过:“几何学里有二个宝库:一个是毕达哥拉斯定理(我们称为“勾股定理”);另外一个就是黄金分割。前者好比黄金,后者堪称珠玉。” 归 纳 小 结 :今天的学习你有何收获和体会!(1)作业本 习题4.3 第1题。(必做题)
(2)利用“黄金分割”的作法画一个“黄金五角星”。
(C层学生必做;A、B层学生选做)作 业:设计说明: 本节课在了解黄金分割后,以积累数学活
动经验来立意,定位在丰富对线段的比、成
比例线段有关数学知识的认识上,从生活中
经常碰到的问题,如何摆放引入,扩展对黄
金分割的认识,欣赏并挖掘生活中存在黄金
分割知识,重点放在了解黄金分割,体会其
中的文化价值上。谢 谢 大 家!发现新知 《黄金分割》学习资料
学习小组名单: 1、测量五角星上C点到A、B点的距离。
AC=
AB=
BC=
2、请你再计算一下和的值分别是多少,它们相等吗?= ,= ,
同课章节目录
