二次函数的图象与性质(2)(河南省郑州市)
文档属性
| 名称 | 二次函数的图象与性质(2)(河南省郑州市) |  | |
| 格式 | rar | ||
| 文件大小 | 95.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-13 07:41:00 | ||
图片预览

文档简介
27.2 二次函数的图象与性质(2)
教学目标 会画出这类函数的图象,通过比较,了解这类函数的性质.
教学重点 通过画图得出二次函数性质
教学难点 识图能力的培养
教学过程
1、 情境导入
1、同学们还记得一次函数与的图象的关系吗?
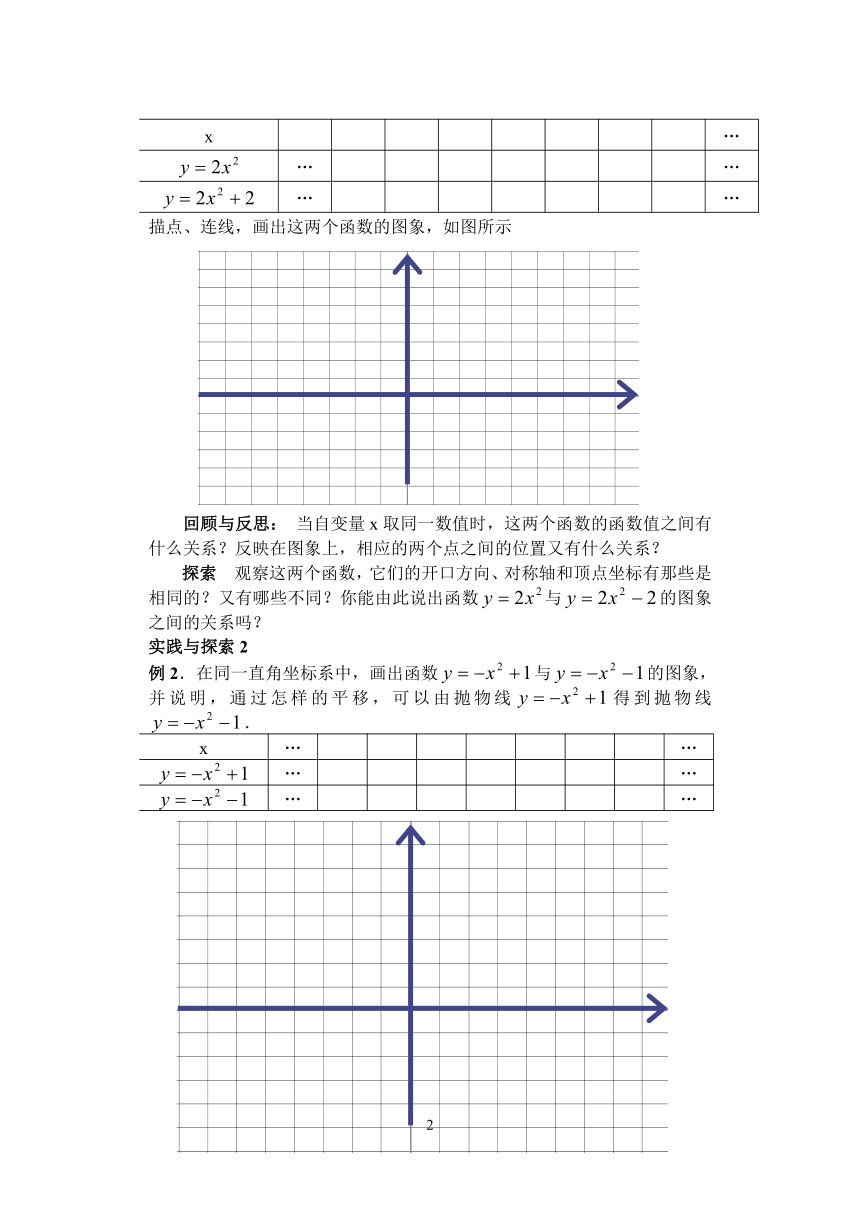
2、比较二次函数 y=x 和 y= –x 图象的异同(如图1):
(图1) (图2)
填空:
抛物线
顶点坐标
对称轴
位 置
开口方向
3、二次函数 y=2x 的图象是什么形状?它与二次函数 y=x 的图象(如图2)有什么相同和不同
4、二次函数 y=2x +1 的图象与二次函数 y=2x 的图象有什么关系?
那么与的图象之间又有何关系?
二、新课讲解
实践与探索1
例1. 在同一直角坐标系中,画出函数与的图象.
例2. 解: 列表.
x …
… …
… …
描点、连线,画出这两个函数的图象,如图所示
回顾与反思: 当自变量x取同一数值时,这两个函数的函数值之间有什么关系?反映在图象上,相应的两个点之间的位置又有什么关系?
探索 观察这两个函数,它们的开口方向、对称轴和顶点坐标有那些是相同的?又有哪些不同?你能由此说出函数与的图象之间的关系吗?
实践与探索2
例2.在同一直角坐标系中,画出函数与的图象,并说明,通过怎样的平移,可以由抛物线得到抛物线.
x … …
… …
… …
探索 如果要得到抛物线,应将抛物线作怎样的平移?
课堂小结:
试说出函数y=ax2+k(a、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
课堂作业:
1.抛物线y=-3x2+5的开口向________,对称轴是_______,顶点坐标________,顶点是最_____点,所以函数有最________值是_____.
2.抛物线y=4x2-1与y轴的交点坐标是_________,与x轴的交点坐标是____
3.把抛物线 向下平移2个单位,可以得到抛物线 ; 向上平移5个单位,可以得到抛物线 ;
4.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值为 。
5.函数y=3x2+5与y=3x2的图象的不同之处是( )
A.对称轴 B.开口方向 C.顶点 D.形状
6.已知抛物线y=2x2–1上有两点(x1,y1 ) ,(x1,y1 )且x1<x2<0,则y1 y2
(填“<”或“>”)
7.已知一个二次函数图像的顶点在y轴上,并且离原点1个单位,图像经过点(–1,0),求该二次函数解析式。
8.已知抛物线 ,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?
9、一条抛物线的开口方向、对称轴与相同,顶点纵坐标是-2,且抛物线经过点(1,1),求这条抛物线的函数关系式.
10、求符合下列条件的抛物线y=ax2-1的函数关系式:
(1)通过点(-3,2);(2)与y=x2的开口大小相同,方向相反;
(3)当x的值由0增加到2时,函数值减少4.
11.一台机器原价60万元,如果每年的折旧率是x,两年后这台机器的价位约为y万元,求y与x的函数关系式.
12.已知抛物线y=mx2+n向下平移2个单位后得到的函数图像是y=3x2-1,求m,n 的值.
11.如图,是一座抛物线形拱桥,水位在AB位置时,水面宽4米,水位上升3米达到警戒线MN位置时 ,水面宽4米,某年发洪水,水位以每小时0.25米的速度上升,求水过警戒线后几小时淹到拱桥顶
PAGE
1
教学目标 会画出这类函数的图象,通过比较,了解这类函数的性质.
教学重点 通过画图得出二次函数性质
教学难点 识图能力的培养
教学过程
1、 情境导入
1、同学们还记得一次函数与的图象的关系吗?
2、比较二次函数 y=x 和 y= –x 图象的异同(如图1):
(图1) (图2)
填空:
抛物线
顶点坐标
对称轴
位 置
开口方向
3、二次函数 y=2x 的图象是什么形状?它与二次函数 y=x 的图象(如图2)有什么相同和不同
4、二次函数 y=2x +1 的图象与二次函数 y=2x 的图象有什么关系?
那么与的图象之间又有何关系?
二、新课讲解
实践与探索1
例1. 在同一直角坐标系中,画出函数与的图象.
例2. 解: 列表.
x …
… …
… …
描点、连线,画出这两个函数的图象,如图所示
回顾与反思: 当自变量x取同一数值时,这两个函数的函数值之间有什么关系?反映在图象上,相应的两个点之间的位置又有什么关系?
探索 观察这两个函数,它们的开口方向、对称轴和顶点坐标有那些是相同的?又有哪些不同?你能由此说出函数与的图象之间的关系吗?
实践与探索2
例2.在同一直角坐标系中,画出函数与的图象,并说明,通过怎样的平移,可以由抛物线得到抛物线.
x … …
… …
… …
探索 如果要得到抛物线,应将抛物线作怎样的平移?
课堂小结:
试说出函数y=ax2+k(a、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
课堂作业:
1.抛物线y=-3x2+5的开口向________,对称轴是_______,顶点坐标________,顶点是最_____点,所以函数有最________值是_____.
2.抛物线y=4x2-1与y轴的交点坐标是_________,与x轴的交点坐标是____
3.把抛物线 向下平移2个单位,可以得到抛物线 ; 向上平移5个单位,可以得到抛物线 ;
4.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值为 。
5.函数y=3x2+5与y=3x2的图象的不同之处是( )
A.对称轴 B.开口方向 C.顶点 D.形状
6.已知抛物线y=2x2–1上有两点(x1,y1 ) ,(x1,y1 )且x1<x2<0,则y1 y2
(填“<”或“>”)
7.已知一个二次函数图像的顶点在y轴上,并且离原点1个单位,图像经过点(–1,0),求该二次函数解析式。
8.已知抛物线 ,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?
9、一条抛物线的开口方向、对称轴与相同,顶点纵坐标是-2,且抛物线经过点(1,1),求这条抛物线的函数关系式.
10、求符合下列条件的抛物线y=ax2-1的函数关系式:
(1)通过点(-3,2);(2)与y=x2的开口大小相同,方向相反;
(3)当x的值由0增加到2时,函数值减少4.
11.一台机器原价60万元,如果每年的折旧率是x,两年后这台机器的价位约为y万元,求y与x的函数关系式.
12.已知抛物线y=mx2+n向下平移2个单位后得到的函数图像是y=3x2-1,求m,n 的值.
11.如图,是一座抛物线形拱桥,水位在AB位置时,水面宽4米,水位上升3米达到警戒线MN位置时 ,水面宽4米,某年发洪水,水位以每小时0.25米的速度上升,求水过警戒线后几小时淹到拱桥顶
PAGE
1
