浙教版数学八上5.5一次函数的简单应用(1)课件(共23张PPT)
文档属性
| 名称 | 浙教版数学八上5.5一次函数的简单应用(1)课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 449.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 16:00:50 | ||
图片预览






文档简介
(共23张PPT)
一次函数的简单应用
——第一课时
学习目标
1.能利用一次函数的图象和性质解决实际问题.
2.会综合运用一次函数的表达式,函数图象以及结合方程(组)等其他数学模型,解决实际问题
图象是
表达式为
一次函数
特征1
特征2
判定1
判定2
y=kx+b
一条直线
怎样判断“两个变量满足一次函数关系?”
函数关系有几种呈现方法?
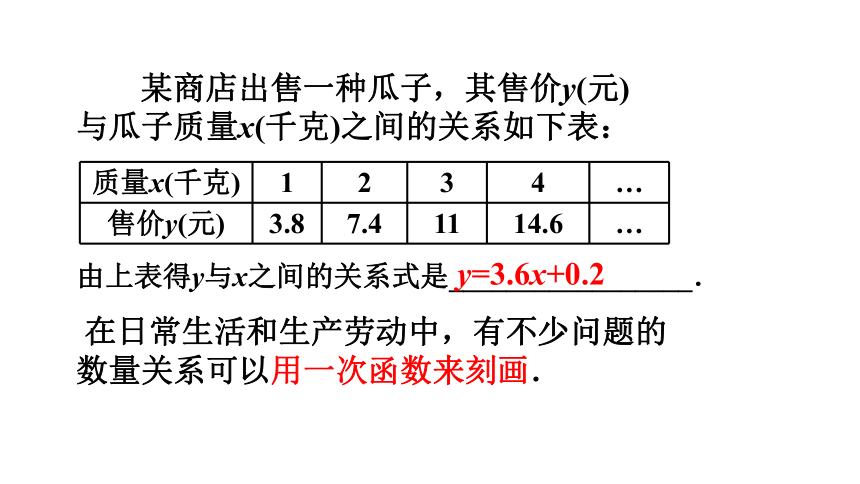
某商店出售一种瓜子,其售价y(元)
与瓜子质量x(千克)之间的关系如下表:
质量x(千克) 1 2 3 4 …
售价y(元) 3.8 7.4 11 14.6 …
由上表得y与x之间的关系式是_________________.
在日常生活和生产劳动中,有不少问题的数量关系可以用一次函数来刻画.
y=3.6x+0.2
在日常生活和生产实践中有不少问题的数量关系可以用一次函数来刻画.在运用一次函数解决实际问题时,首先判定问题中的两个变量之间是不是一次函数关系.当确定是一次函数关系时,可求出函数表达式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
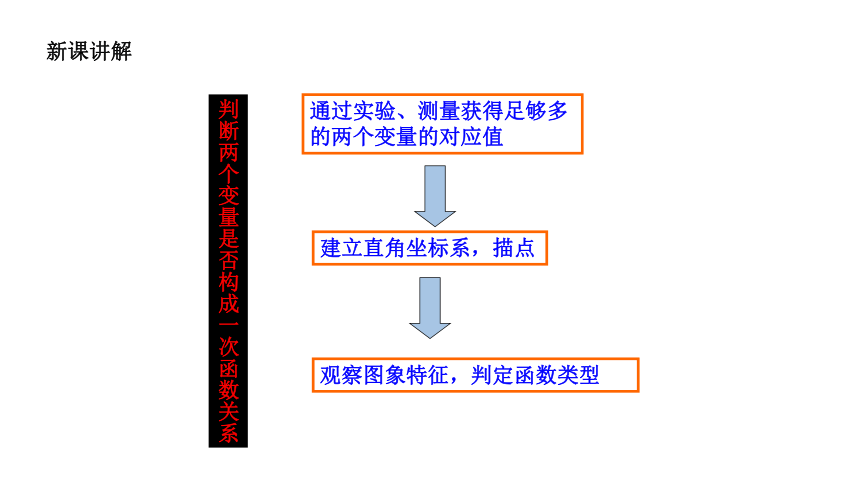
通过实验、测量获得足够多的两个变量的对应值
建立直角坐标系,描点
观察图象特征,判定函数类型
判断两个变量是否构成一次函数关系
新课讲解
x
例1.生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表(单位:米):
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10 10.25 10.72 11.52 12.5 13.16 13.9
问:能否用一次函数刻画这两个变量x与y的关系?如果能,请求出这个函数的解析式.
新课讲解
o
1 2 3 4 5
2
4
6
8
10
12
14
16
18
20
y(m)
x(米)
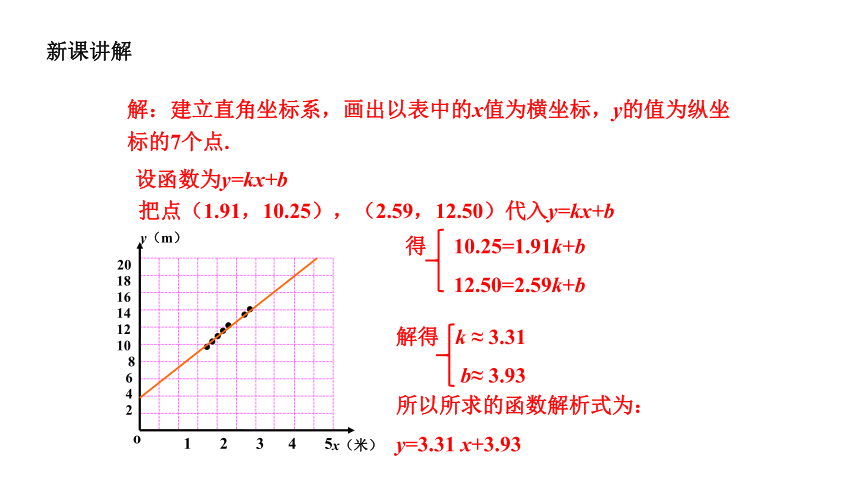
把点(1.91,10.25),(2.59,12.50)代入y=kx+b
设函数为y=kx+b
所以所求的函数解析式为:
y=3.31 x+3.93
解:建立直角坐标系,画出以表中的x值为横坐标,y的值为纵坐标的7个点.
得 10.25=1.91k+b
12.50=2.59k+b
解得 k ≈ 3.31
b≈ 3.93
新课讲解
把其余5个点的坐标代入函数表达式进行检验,你发现了什么问题?
用其他点坐标做出的结果答案不一样
用这样的方法获得的函数有时是近似的!!
新课讲解
描点连线
近似猜测
求解析式
代入验证
写出结论
获取数据
课后总结
蟋蟀叫次数 … 84 98 119 …
温度(℃) … 15 17 20 …
在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系.下面是蟋蟀所叫次数与温度变化情况对照表:
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1分钟叫了63次,那么该地当时的温度大约为多少摄氏度?
学以致用
(1)设蟋蟀1分钟叫的次数为x次,当地温度为y摄氏度,一次函数关系式为y=kx+b,由题意,得
15=84k+b
17=98k+b
解得k=,b=3∴y=x+3;
(2)当x=63时,y=x+3=12
答:蟋蟀1分钟叫了63次,该地当时温度为12摄氏度.
学以致用
1.小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是_____分钟
先算出平路、上坡路和下坡路的速度分别为、和(千米/分),
所以他从单位到家门口需要的时间是2÷+1÷+1÷=15(分钟).
故答案为:15.
15
巩固练习
2.弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
x(kg) 0 1 2 3 4 …..
y(cm) …..
问:(1)能否用一次函数刻画这两个变量y与x的关系?如果能,请求出这个函数的解析式.
(2)当x=8时,y的值是多少
6.0
7.1
7.6
6.4
8.1
o
1 2 3 4 5
2
4
6
8
10
y(cm)
x(kg)
把表格中的点在坐标系中描出来.
巩固练习
解:(1)设一次函数为y=kx+b,将(0,6.0)(1,6.4)代入y=kx+b,得:
6.0=b
6.4= k+b
解得: k=0.4
b=6
∴函数解析式为y=0.4x+6
(2)当x=8时,y=0.4×8+6=9.2
巩固练习
3.如图,反映了小明从家到超市购物的全过程,时间与距家路程之间关系如图.
(1)图中反映了哪两个变量之间的关系?超市离家多远?
(2)小明在超市待了多少时间小明从超市回到家花了多少时间?
(3)小明从家到超市时的平均速度是多少?
(4)求返回时距离与时间(分)之间的函数关系式.
巩固练习
(1)图中反映了距离与时间之间的关系;超市离家900米;
(2)小明在超市待了30-20=10分钟,小明从超市回到家花了45-30=15分钟;
(3)小明从家到超市的平均速度是900÷20=45米/分钟;
(4)设函数关系式为y=kx+b,
则 30k+b=900
45k+b=0
解得 k=-60
b=2700,
∴y=-60x+2700(30≤t≤45).
巩固练习
4.已知一次函数图象经过A(2,1)和点B(-2,5).
(1)求这个一次函数的解析式,并画出这个函数的图象
(2)求此函数的图象与坐标轴围成的三角形的面积.
解:(1)设函数解析式为y=kx+b,将A(2,1)和B(-2,5)代入得:
1=2k+b
5=-2k+b,
解得: k=-1
b=3,
∴函数解析式为:y=-x+3.
与x轴交点为(3,0),与y轴交点为(0,3),所作图形为:
(2)面积=×3×3=.
巩固练习
5.小丽一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,行驶若干小时后,中途在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题:
(1)汽车行驶______h后加油,中途加油______L;
(2)求加油前油箱余没油量Q与行驶时间t之间的函数关系式;
(3)如果加油站距景点200 km,车速为80 km/h,要到达目的地,油箱中的油是否够用?请说明理由.
3
24
巩固练习
(1)从图中可知汽车行驶3h后加油,中途加油24L;
(2)根据分析可知Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
∵200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴油箱中的油是够用的.
巩固练习
(春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”,由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害)某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系,请你根据图中信息,针对这种植物判断次日是否需要采取霜冻措施,并说明理由.
拓展提升
解:根据图象可知:0时-5时的一次函数关系式为y1=-+3,
5时-8时的一次函数关系式y2=--,当y1、y2分别为0时,
x1=,x2=.而|x2-x1|=>3,(相当于求MN的距离)
∴应采取防霜冻措施.
拓展提升
这节课我们学习了:
确定两个变量是否构成一次函数关系的步骤:
(1)通过实验、测量获得数量足够多的两个变量的对应值
(2)建立合适的直角坐标系,描点画函数图象
(3)观察图象特征,判定函数的类型
这种方法获得的表达式有时是近似的.
课堂小结
一次函数的简单应用
——第一课时
学习目标
1.能利用一次函数的图象和性质解决实际问题.
2.会综合运用一次函数的表达式,函数图象以及结合方程(组)等其他数学模型,解决实际问题
图象是
表达式为
一次函数
特征1
特征2
判定1
判定2
y=kx+b
一条直线
怎样判断“两个变量满足一次函数关系?”
函数关系有几种呈现方法?
某商店出售一种瓜子,其售价y(元)
与瓜子质量x(千克)之间的关系如下表:
质量x(千克) 1 2 3 4 …
售价y(元) 3.8 7.4 11 14.6 …
由上表得y与x之间的关系式是_________________.
在日常生活和生产劳动中,有不少问题的数量关系可以用一次函数来刻画.
y=3.6x+0.2
在日常生活和生产实践中有不少问题的数量关系可以用一次函数来刻画.在运用一次函数解决实际问题时,首先判定问题中的两个变量之间是不是一次函数关系.当确定是一次函数关系时,可求出函数表达式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
通过实验、测量获得足够多的两个变量的对应值
建立直角坐标系,描点
观察图象特征,判定函数类型
判断两个变量是否构成一次函数关系
新课讲解
x
例1.生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表(单位:米):
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10 10.25 10.72 11.52 12.5 13.16 13.9
问:能否用一次函数刻画这两个变量x与y的关系?如果能,请求出这个函数的解析式.
新课讲解
o
1 2 3 4 5
2
4
6
8
10
12
14
16
18
20
y(m)
x(米)
把点(1.91,10.25),(2.59,12.50)代入y=kx+b
设函数为y=kx+b
所以所求的函数解析式为:
y=3.31 x+3.93
解:建立直角坐标系,画出以表中的x值为横坐标,y的值为纵坐标的7个点.
得 10.25=1.91k+b
12.50=2.59k+b
解得 k ≈ 3.31
b≈ 3.93
新课讲解
把其余5个点的坐标代入函数表达式进行检验,你发现了什么问题?
用其他点坐标做出的结果答案不一样
用这样的方法获得的函数有时是近似的!!
新课讲解
描点连线
近似猜测
求解析式
代入验证
写出结论
获取数据
课后总结
蟋蟀叫次数 … 84 98 119 …
温度(℃) … 15 17 20 …
在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系.下面是蟋蟀所叫次数与温度变化情况对照表:
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1分钟叫了63次,那么该地当时的温度大约为多少摄氏度?
学以致用
(1)设蟋蟀1分钟叫的次数为x次,当地温度为y摄氏度,一次函数关系式为y=kx+b,由题意,得
15=84k+b
17=98k+b
解得k=,b=3∴y=x+3;
(2)当x=63时,y=x+3=12
答:蟋蟀1分钟叫了63次,该地当时温度为12摄氏度.
学以致用
1.小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是_____分钟
先算出平路、上坡路和下坡路的速度分别为、和(千米/分),
所以他从单位到家门口需要的时间是2÷+1÷+1÷=15(分钟).
故答案为:15.
15
巩固练习
2.弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
x(kg) 0 1 2 3 4 …..
y(cm) …..
问:(1)能否用一次函数刻画这两个变量y与x的关系?如果能,请求出这个函数的解析式.
(2)当x=8时,y的值是多少
6.0
7.1
7.6
6.4
8.1
o
1 2 3 4 5
2
4
6
8
10
y(cm)
x(kg)
把表格中的点在坐标系中描出来.
巩固练习
解:(1)设一次函数为y=kx+b,将(0,6.0)(1,6.4)代入y=kx+b,得:
6.0=b
6.4= k+b
解得: k=0.4
b=6
∴函数解析式为y=0.4x+6
(2)当x=8时,y=0.4×8+6=9.2
巩固练习
3.如图,反映了小明从家到超市购物的全过程,时间与距家路程之间关系如图.
(1)图中反映了哪两个变量之间的关系?超市离家多远?
(2)小明在超市待了多少时间小明从超市回到家花了多少时间?
(3)小明从家到超市时的平均速度是多少?
(4)求返回时距离与时间(分)之间的函数关系式.
巩固练习
(1)图中反映了距离与时间之间的关系;超市离家900米;
(2)小明在超市待了30-20=10分钟,小明从超市回到家花了45-30=15分钟;
(3)小明从家到超市的平均速度是900÷20=45米/分钟;
(4)设函数关系式为y=kx+b,
则 30k+b=900
45k+b=0
解得 k=-60
b=2700,
∴y=-60x+2700(30≤t≤45).
巩固练习
4.已知一次函数图象经过A(2,1)和点B(-2,5).
(1)求这个一次函数的解析式,并画出这个函数的图象
(2)求此函数的图象与坐标轴围成的三角形的面积.
解:(1)设函数解析式为y=kx+b,将A(2,1)和B(-2,5)代入得:
1=2k+b
5=-2k+b,
解得: k=-1
b=3,
∴函数解析式为:y=-x+3.
与x轴交点为(3,0),与y轴交点为(0,3),所作图形为:
(2)面积=×3×3=.
巩固练习
5.小丽一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,行驶若干小时后,中途在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题:
(1)汽车行驶______h后加油,中途加油______L;
(2)求加油前油箱余没油量Q与行驶时间t之间的函数关系式;
(3)如果加油站距景点200 km,车速为80 km/h,要到达目的地,油箱中的油是否够用?请说明理由.
3
24
巩固练习
(1)从图中可知汽车行驶3h后加油,中途加油24L;
(2)根据分析可知Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
∵200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴油箱中的油是够用的.
巩固练习
(春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”,由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害)某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系,请你根据图中信息,针对这种植物判断次日是否需要采取霜冻措施,并说明理由.
拓展提升
解:根据图象可知:0时-5时的一次函数关系式为y1=-+3,
5时-8时的一次函数关系式y2=--,当y1、y2分别为0时,
x1=,x2=.而|x2-x1|=>3,(相当于求MN的距离)
∴应采取防霜冻措施.
拓展提升
这节课我们学习了:
确定两个变量是否构成一次函数关系的步骤:
(1)通过实验、测量获得数量足够多的两个变量的对应值
(2)建立合适的直角坐标系,描点画函数图象
(3)观察图象特征,判定函数的类型
这种方法获得的表达式有时是近似的.
课堂小结
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
