浙教版数学八上2.7探索勾股定理(1) 课件(共23张PPT)
文档属性
| 名称 | 浙教版数学八上2.7探索勾股定理(1) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 712.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 16:14:30 | ||
图片预览





文档简介
(共23张PPT)
探索勾股定理
浙教版 八年级上
——第一课时
学习目标
1.了解拼图验证勾股定理的方法;
2.掌握勾股定理,会利用两边边长求直角三角形的另一边长;
3.会利用勾股定理解决实际问题.
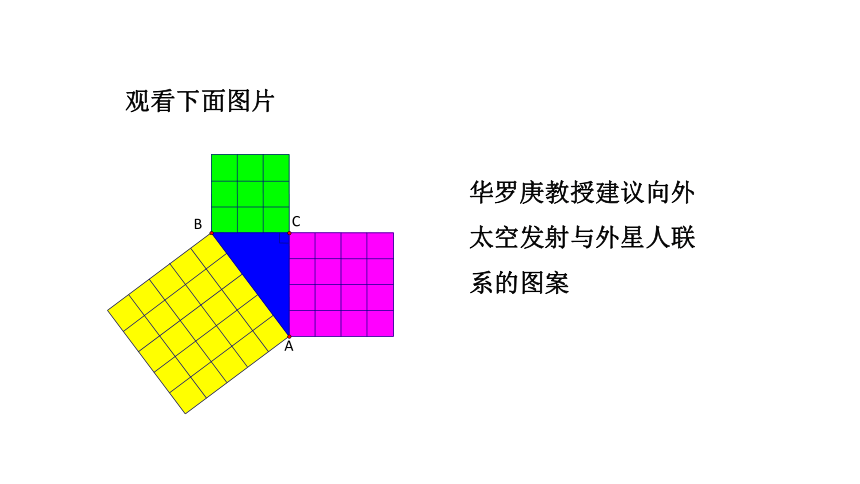
观看下面图片
C
B
A
华罗庚教授建议向外太空发射与外星人联系的图案
合作学习
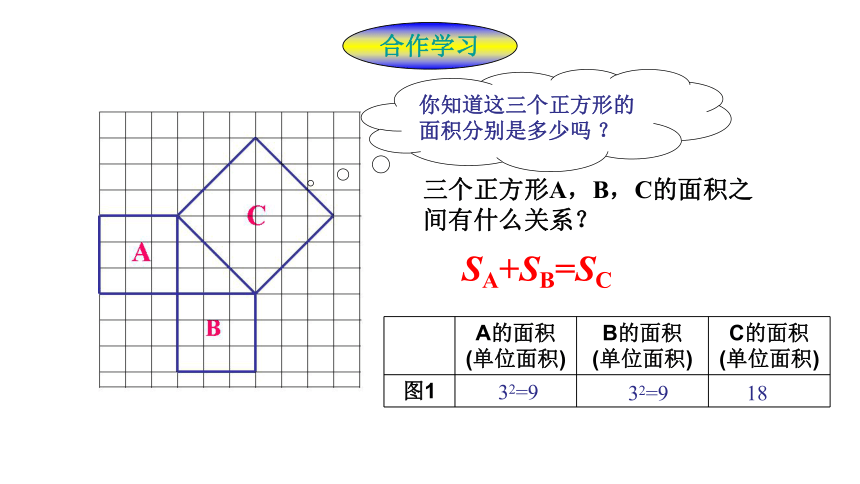
你知道这三个正方形的面积分别是多少吗 ?
三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图1
32=9
32=9
18
如图是在北京召开的第24届国际数学家大会(ICM—2002) 的会标.它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图.用弦图证明勾股定理在数学史上有着重要的地位.
导入新课
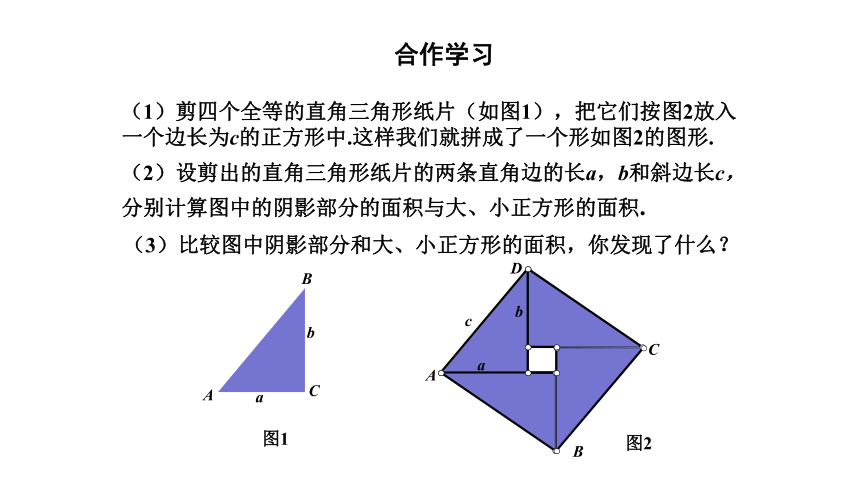
(1)剪四个全等的直角三角形纸片(如图1),把它们按图2放入一个边长为c的正方形中.这样我们就拼成了一个形如图2的图形.
(3)比较图中阴影部分和大、小正方形的面积,你发现了什么?
(2)设剪出的直角三角形纸片的两条直角边的长a,b和斜边长c,分别计算图中的阴影部分的面积与大、小正方形的面积.
b
a
B
A
C
图1
b
a
c
D
A
C
B
图2
合作学习
a2+b2=c2
大正方形的面积:c
小正方形面积:(b-a)
阴影部分面积:4×ab
它们之间的关系是:
化简得:
直角三角形三边有下面的关系:
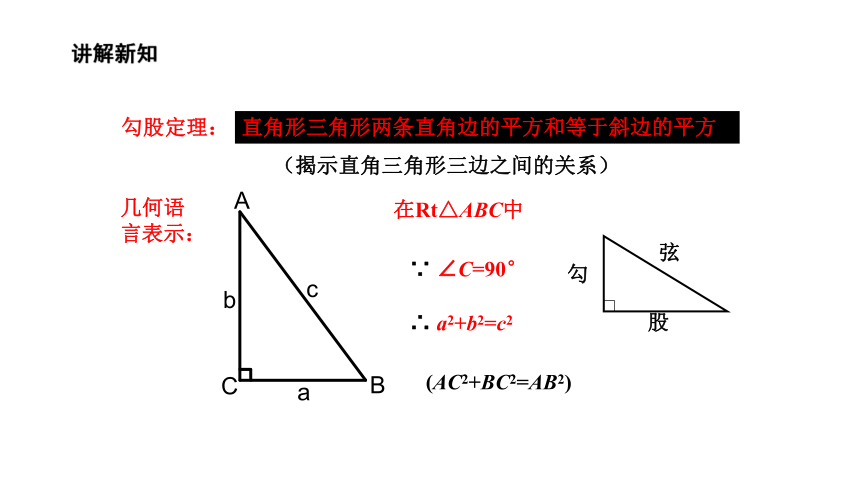
直角三角形两条直角边的平方和等于斜边的平方
合作学习
勾股定理:
直角形三角形两条直角边的平方和等于斜边的平方.
∴ a2+b2=c2
在Rt△ABC中
∵ ∠C=90°
(AC2+BC2=AB2)
勾
股
弦
(揭示直角三角形三边之间的关系)
几何语言表示:
讲解新知
(1)若a=1, b=2, 求c;
例1:已知ΔABC中,∠C=Rt∠,BC=a, AC=b,AB=c.
(2)若a=15,c=17,求b;
解:(1)根据勾股定理,得c =a +b =1 +2 =5
∵c>0,∴c=
(2)根据勾股定理,得b =c -a =17 -5 =64
∵b>0,∴b=8
例题讲解
1.如果一个直角三角形的两条直角边分别为n2-1,2n(n>1),那么它的斜边长是( )
A.2n B.n+1 C.n2-1 D.n2+1
解:两条直角边与斜边满足勾股定理,则斜边长是:==n +1
D
2.在直角三角形中,已知其中两边分别为3和4,则第三边等于__________.
解:当此直角三角形的两直角边分别是3和4时,
则第三边为==5,
当此直角三角形的一个直角边为3,斜边为4时,
则第三边为==.
5或
即时演练
例2 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
C
160
90
40
40
B
A
解:过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理,得
AB =AC +BC
=50 +120 =16900(mm )
例题讲解
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm
C
160
90
40
40
B
A
m
例题讲解
铁路上A、B两站(视为直线上两点)相距25km,C、D为两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站______km处.
10
m
即时演练
解:∵C、D两村到E站距离相等,∴CE=DE,
在Rt△DAE和Rt△CBE中,DE2=AD2+AE2,CE2=BE2+BC2,
∴AD2+AE2=BE2+BC2.
设AE为x,则BE=25-x,
将BC=10,DA=15代入关系式为x2+152=(25-x)2+102,
整理得,50x=500,
解得x=10,
∴E站应建在距A站10km处.
即时演练
1.下列几组数据:(1)8,15,17; (2)7,12,15;(3)12,15,20;(4)7,24,25.其中是勾股数组的有几组( )
A.1 B.2 C.3 D.4
解:(1)∵82+152=64+225=289,172=289,
∴82+152=172,即8,15,17是一组勾股数;
(2)∵72+122=49+144=193,152=225,
∴72+122≠152,即7,12,15不是一组勾股数;
(3)∵122+152=144+225=369,202=400,
∴122+152≠202,即12,15,20不是一组勾股数;
(4)∵72+242=49+576=625,252=625,
∴72+242=252,即7,24,25是一组勾股数,
则其中勾股数有2组.
故选B.
B
达标测评
2.如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯______米.
解:在直角三角形AOB中,根据勾股定理,得:
OB=6m,
根据题意,得:OB′=6+2=8m.
又∵梯子的长度不变,
在Rt△A′OB′中,根据勾股定理,得:OA′=6m.
则AA′=8-6=2m.
2
达标测评
3.如图,△ABC中,∠BAC=90°,且AB=AC,将△ABP绕点A旋转到△ACP′的位置,若AP=3,则PP′=______.
解:依题意,得旋转角∠PAP′=∠BAC=90°,AP=AP′=3,
∴△APP′为等腰直角三角形,
∴PP′= =3 .
故本题答案为:3 .
3
达标测评
4.已知∠C=90°,BC=3cm,BD=12cm, AD=13cm.△ABC的面积是6cm2.
(1)求AB的长度;
(2)求△ABD的面积.
解:(1)∵∠C=90°
∴S△ABC=×BC×AC=6,
∴AC=4(cm).
∵BC2+AC2=AB2,
∴AB===5(cm).
(2)∵AB2+BD2=52+122=169,AD2=132=169,
∴AB2+BD2=AD2.
∴∠ABD=90°.
∴S△ABD=×AB×BD=×5×12=30(cm2).
m
达标测评
5.如图所示,正四棱柱的底面边长为5 cm,侧棱长为 8 cm,一只蚂蚁欲从正四棱柱底面上的顶点 A沿棱柱的表面爬到顶点C'处吃食物. 那么它需要爬行的最短路程的长是多少?
解:(1)沿侧枝 BB',将侧面A'B和侧面B'C展开如图1所示,连接AC'.
∵AB=BC=5 cm,CC'=8 cm,
由勾股定理,得= =
达标测评
∴易知沿 DC展开和DD'展开的情况同上述两种情况一致.
又∵ >=2
∴蚂蚁需要爬行的最短路轻的长为2cm
(2)沿底边A‘B’. 将底面A‘C’和侧面A‘B展开如图2所示,连接 AC’.
∵AB=5cm,BC’=BB’+B’C’=8+5=13cm,
由勾股定理,得= = (cm)
达标测评
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
证明:(1)连接AC.
∵∠ABC=90°,
∴AB2+BC2=AC2.
∵CD⊥AD,
∴AB=BC.
∴AD2+CD2=AC2.
∵AD2+CD2=2AB2,
∴AB2+BC2=2AB2,
∴BC2=AB2,
拓展提升
(2)过C作CF⊥BE于F.
∵BE⊥AD,CF⊥BE,CD⊥AD,
∴∠FED=∠CFE=∠D=90°,
∴四边形CDEF是矩形.
∴CD=EF.
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
∴在△BAE与△CBF中,
∠AEB=∠BFC
∠BAE=∠CBF
AB=BC
∴△BAE≌△CBF .(AAS)
∴AE=BF.
∴BE=BF+EF=AE+CD.
m
拓展提升
这节课我们学习了:
1.勾股定理的证明
2.勾股定理
3.勾股定理的应用
m
探索勾股定理
浙教版 八年级上
——第一课时
学习目标
1.了解拼图验证勾股定理的方法;
2.掌握勾股定理,会利用两边边长求直角三角形的另一边长;
3.会利用勾股定理解决实际问题.
观看下面图片
C
B
A
华罗庚教授建议向外太空发射与外星人联系的图案
合作学习
你知道这三个正方形的面积分别是多少吗 ?
三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图1
32=9
32=9
18
如图是在北京召开的第24届国际数学家大会(ICM—2002) 的会标.它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图.用弦图证明勾股定理在数学史上有着重要的地位.
导入新课
(1)剪四个全等的直角三角形纸片(如图1),把它们按图2放入一个边长为c的正方形中.这样我们就拼成了一个形如图2的图形.
(3)比较图中阴影部分和大、小正方形的面积,你发现了什么?
(2)设剪出的直角三角形纸片的两条直角边的长a,b和斜边长c,分别计算图中的阴影部分的面积与大、小正方形的面积.
b
a
B
A
C
图1
b
a
c
D
A
C
B
图2
合作学习
a2+b2=c2
大正方形的面积:c
小正方形面积:(b-a)
阴影部分面积:4×ab
它们之间的关系是:
化简得:
直角三角形三边有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方
合作学习
勾股定理:
直角形三角形两条直角边的平方和等于斜边的平方.
∴ a2+b2=c2
在Rt△ABC中
∵ ∠C=90°
(AC2+BC2=AB2)
勾
股
弦
(揭示直角三角形三边之间的关系)
几何语言表示:
讲解新知
(1)若a=1, b=2, 求c;
例1:已知ΔABC中,∠C=Rt∠,BC=a, AC=b,AB=c.
(2)若a=15,c=17,求b;
解:(1)根据勾股定理,得c =a +b =1 +2 =5
∵c>0,∴c=
(2)根据勾股定理,得b =c -a =17 -5 =64
∵b>0,∴b=8
例题讲解
1.如果一个直角三角形的两条直角边分别为n2-1,2n(n>1),那么它的斜边长是( )
A.2n B.n+1 C.n2-1 D.n2+1
解:两条直角边与斜边满足勾股定理,则斜边长是:==n +1
D
2.在直角三角形中,已知其中两边分别为3和4,则第三边等于__________.
解:当此直角三角形的两直角边分别是3和4时,
则第三边为==5,
当此直角三角形的一个直角边为3,斜边为4时,
则第三边为==.
5或
即时演练
例2 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
C
160
90
40
40
B
A
解:过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理,得
AB =AC +BC
=50 +120 =16900(mm )
例题讲解
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm
C
160
90
40
40
B
A
m
例题讲解
铁路上A、B两站(视为直线上两点)相距25km,C、D为两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站______km处.
10
m
即时演练
解:∵C、D两村到E站距离相等,∴CE=DE,
在Rt△DAE和Rt△CBE中,DE2=AD2+AE2,CE2=BE2+BC2,
∴AD2+AE2=BE2+BC2.
设AE为x,则BE=25-x,
将BC=10,DA=15代入关系式为x2+152=(25-x)2+102,
整理得,50x=500,
解得x=10,
∴E站应建在距A站10km处.
即时演练
1.下列几组数据:(1)8,15,17; (2)7,12,15;(3)12,15,20;(4)7,24,25.其中是勾股数组的有几组( )
A.1 B.2 C.3 D.4
解:(1)∵82+152=64+225=289,172=289,
∴82+152=172,即8,15,17是一组勾股数;
(2)∵72+122=49+144=193,152=225,
∴72+122≠152,即7,12,15不是一组勾股数;
(3)∵122+152=144+225=369,202=400,
∴122+152≠202,即12,15,20不是一组勾股数;
(4)∵72+242=49+576=625,252=625,
∴72+242=252,即7,24,25是一组勾股数,
则其中勾股数有2组.
故选B.
B
达标测评
2.如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯______米.
解:在直角三角形AOB中,根据勾股定理,得:
OB=6m,
根据题意,得:OB′=6+2=8m.
又∵梯子的长度不变,
在Rt△A′OB′中,根据勾股定理,得:OA′=6m.
则AA′=8-6=2m.
2
达标测评
3.如图,△ABC中,∠BAC=90°,且AB=AC,将△ABP绕点A旋转到△ACP′的位置,若AP=3,则PP′=______.
解:依题意,得旋转角∠PAP′=∠BAC=90°,AP=AP′=3,
∴△APP′为等腰直角三角形,
∴PP′= =3 .
故本题答案为:3 .
3
达标测评
4.已知∠C=90°,BC=3cm,BD=12cm, AD=13cm.△ABC的面积是6cm2.
(1)求AB的长度;
(2)求△ABD的面积.
解:(1)∵∠C=90°
∴S△ABC=×BC×AC=6,
∴AC=4(cm).
∵BC2+AC2=AB2,
∴AB===5(cm).
(2)∵AB2+BD2=52+122=169,AD2=132=169,
∴AB2+BD2=AD2.
∴∠ABD=90°.
∴S△ABD=×AB×BD=×5×12=30(cm2).
m
达标测评
5.如图所示,正四棱柱的底面边长为5 cm,侧棱长为 8 cm,一只蚂蚁欲从正四棱柱底面上的顶点 A沿棱柱的表面爬到顶点C'处吃食物. 那么它需要爬行的最短路程的长是多少?
解:(1)沿侧枝 BB',将侧面A'B和侧面B'C展开如图1所示,连接AC'.
∵AB=BC=5 cm,CC'=8 cm,
由勾股定理,得= =
达标测评
∴易知沿 DC展开和DD'展开的情况同上述两种情况一致.
又∵ >=2
∴蚂蚁需要爬行的最短路轻的长为2cm
(2)沿底边A‘B’. 将底面A‘C’和侧面A‘B展开如图2所示,连接 AC’.
∵AB=5cm,BC’=BB’+B’C’=8+5=13cm,
由勾股定理,得= = (cm)
达标测评
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
证明:(1)连接AC.
∵∠ABC=90°,
∴AB2+BC2=AC2.
∵CD⊥AD,
∴AB=BC.
∴AD2+CD2=AC2.
∵AD2+CD2=2AB2,
∴AB2+BC2=2AB2,
∴BC2=AB2,
拓展提升
(2)过C作CF⊥BE于F.
∵BE⊥AD,CF⊥BE,CD⊥AD,
∴∠FED=∠CFE=∠D=90°,
∴四边形CDEF是矩形.
∴CD=EF.
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
∴在△BAE与△CBF中,
∠AEB=∠BFC
∠BAE=∠CBF
AB=BC
∴△BAE≌△CBF .(AAS)
∴AE=BF.
∴BE=BF+EF=AE+CD.
m
拓展提升
这节课我们学习了:
1.勾股定理的证明
2.勾股定理
3.勾股定理的应用
m
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
