浙教版八年级数学上册试题 3.4 一元一次不等式组同步练习(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 3.4 一元一次不等式组同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 109.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-10 01:57:40 | ||
图片预览

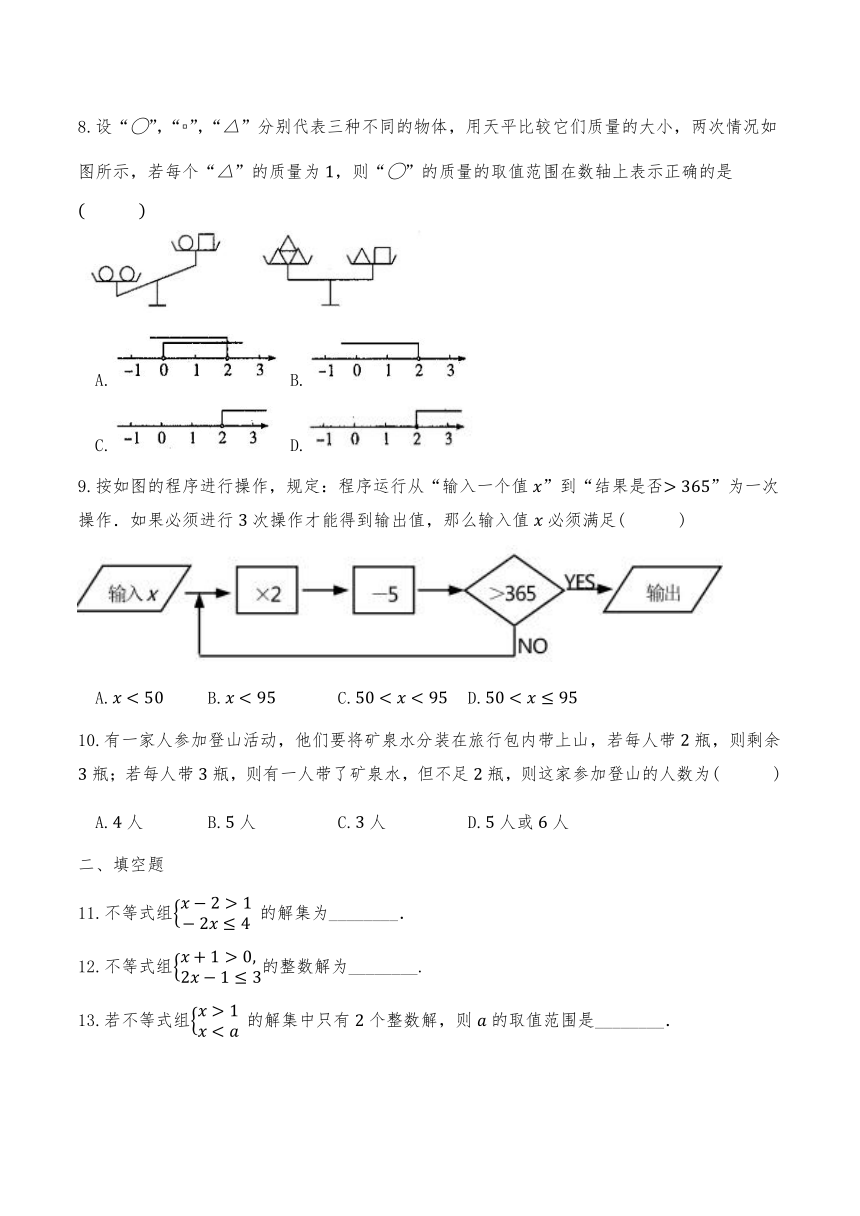



文档简介
3.4 一元一次不等式组
第一课时
一、选择题
1.下列选项中是一元一次不等式组的是( )
A. B. C. D.
2.下列说法正确的是( )
A.不等式组的解集是 B.的解集是
C.的解集是= D.的解集是
3.不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
4.若不等式组的解为,则的取值范围是( )
A. B. C. D.
5.已知不等式组的解集为,则值为( )
A. B. C. D.
6.不等式组的解集为,则的取值范围为( )
A. B. C. D.
7.已知关于的不等式组 有个整数解,则符合条件的所有整数的个数为( )
A. B. C. D.
8.设“”,“”,“”分别代表三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,若每个“”的质量为,则“”的质量的取值范围在数轴上表示正确的是
A. B.
C. D.
9.按如图的程序进行操作,规定:程序运行从“输入一个值”到“结果是否”为一次操作.如果必须进行次操作才能得到输出值,那么输入值必须满足( )
A. B. C. D.
10.有一家人参加登山活动,他们要将矿泉水分装在旅行包内带上山,若每人带瓶,则剩余瓶;若每人带瓶,则有一人带了矿泉水,但不足瓶,则这家参加登山的人数为( )
A.人 B.人 C.人 D.人或人
二、填空题
11.不等式组的解集为________.
12.不等式组的整数解为________.
13.若不等式组的解集中只有个整数解,则的取值范围是________.
14.不等式组的最大整数解为________.
15.已知不等式组,是非负整数,则的值为________.
三、解答题
16.解下列不等式(或不等式组),并把解集表示在数轴上:
(1); (2).
17.
(1)解不等式,并把解集在数轴上表示出来.
(2)解不等式组并写出它的所有整数解.
18. 解不等式(组):
(1)解不等式,并把它的解集在数轴上表示出来.
(2)解不等式组,并写出它的所有整数解.
19.已知.
化简;
①若满足不等式组从中选择合适的的整数值代入求的值;
②若代数式的值为,求的值.
20. 某手机专营店代理销售,两种型号手机.手机的进价、售价如下表:
型 号
进 价 元/部 元/部
售 价 元/部 元/部
第一个月:用元购进,两种型号的手机,全部售完后获利元,求第一个月购进,两种型号手机的数量;
第二个月:计划购进,两种型号手机共部,且不超出第一个月购进,两种型号的手机总费用,则型号手机最多能购多少部?
第二课时
一、选择题
1.是不小于的负数,表示为( )
A. B.
C. D.
2.小明要制作一个长方形的相片框架,这个框架的长为,面积不小于,则宽的长度应满足的不等式组为( )
A. B. C. D.
3.将一箱苹果分给若干个小朋友,若每位小朋友分个苹果,则还剩个苹果;若每位小朋友分个苹果,则有-个小朋友分到苹果但不到个苹果.求这一箱苹果的个数与小朋友的人数.若设有人,则可列不等式为( )
A. B.
C. D.
4.小颖同学准备用元买笔和笔记本,已知一支笔元,一本笔记本元,他买了本笔记本,最多还能买多少支笔?设他还能买支笔,则列出的不等式为( )
A. B.
C. D.
5.如图,这是王彬同学设计的一个计算机程序,规定从“输入一个值”到判断“结果是否”为一次运行过程.如果程序运行两次就停止,那么的取值范围是( )
A. B. C. D.
6.有不足个苹果分给若干个小朋友,若每个小朋友分个,则剩个苹果;若每个小朋友分个,则有一个小朋友没分到苹果,且最后一个分到苹果的小朋友分得的苹果数不足个.已知小朋友人数是偶数个,那么苹果的个数是( )
A. B. C. D.
7.有一家人参加登山活动,他们要将矿泉水分装在旅行包内带上山,若每人带瓶,则剩余瓶;若每人带瓶,则有一人带了矿泉水,但不足瓶,则这家参加登山的人数为( )
A.人 B.人 C.人 D.人或人
8.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人盒牛奶,那么剩下盒牛奶;如果分给每位老人盒牛奶,那么最后一位老人分得的牛奶不足盒,但至少盒,则这个敬老院的老人最少有( )
A.人 B.人 C.人 D.人
9.小明去商店购买,两种玩具,共用了元钱,种玩具每件元,种玩具每件元.若每种玩具至少买一件,且种玩具的数量多于种玩具的数量.则小明的购买方案有( )
A.种 B.种 C.种 D.种
二、填空题
10.列不等式组:与的和小于,且与的差是负数________.
11.把一批书分给小朋友,每人本,则余本;每人本,则最后一个小朋友得到书且不足本,则共有小朋友________人.
12.把颗糖平均分成若干份,每份不得少于颗,也不能多于颗,那么一共有________种不同分法.
13.某运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作.如果程序操作进行了两次才停止,那么的取值范围是________.
14.大连某中学七年级网络班级计划将全班同学分成若干小组,开展数学探究活动,若每个小组人,则还余人,若每个小组人,则有一个小组的人数不足人,但多于人,则该班学生的人数是________.
15.若干名学生住宿舍,每间住人,人无处住;每间住人,空一间还有一间不空也不满,问多少学生多少宿舍?设有间宿舍,则可列不等式(组)为________.
三、解答题
16. 学校购进一批节能灯,已知只型节能灯和只型节能灯共需元;只型节能灯和只型节能灯共需元
(1)求一只型节能灯和一只型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共只,并且型节能灯的数量不多于型节能灯数量的倍,不少于型节能灯数量的倍,有几种购买方案,哪种方案最省钱?
17.某商场经销甲、乙两种商品,甲种商品每件进价元,售价元;乙种商品每件进价元,售价元.
(1)若该商场同时购进甲、乙两种商品共件恰好用去元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共件的总利润(利润=售价一进价)不少于元,且甲商品的件数不能低于件,请你帮忙求出该商场有几种进货方案?
18. 某小区准备新建个停车位,以解决小区停车难的问题.已知新建个地上停车位和个地下停车位共需万元;新建个地上停车位和个地下停车位共需万元.
(1)该小区新建个地上停车位和个地下停车位各需多少万元?
(2)若该小区新建车位的投资金额超过万元而不超过万元,问共有几种建造方案?
(3)对(2)中的几种建造方案中,哪一种方案的投资最少?并求出最少投资金额.
19.我市在创建全国文明城市过程中,决定购买,两种树苗对某路段道路进行绿化改造,已知购买种树苗棵,种树苗棵,需要元;若购买种树苗棵,种树苗棵,则需要元.
(1)求购买,两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进种树苗不能少于棵,且用于购买这两种树苗的资金不能超过元,若购进这两种树苗共棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵种树苗可获工钱元,种好一棵种树苗可获工钱元,在第(2)问的各种购买方案中,种好这棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
第一课时答案
一、选择题
D.C.A.A.B.C.A.C.D.B
二、填空题
11.
12.,,
13.
14.
15.
三、解答题
16.(1)
去分母得,,
去括号得,,
移项得,,
合并同类项得,,
把的系数化为得,.
在数轴上表示为:
;
(2),
由①得,,
由②得,,
故不等式组的解集为:.
在数轴上表示为:
.
17.去分母,得:,
去括号,得:,
移项、合并,得:,
将不等式的解集表示在数轴上如下:
由得:,
由得:,
不等式组的解集是,
∴ 所有整数解是,,.
18.去分母,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为,得:,
将解集表示在数轴上如下:
解不等式,得:,
解不等式,得:,
则不等式组的解集为,
所以不等式组的整数解为、、.
19.
解:.
(2)①解得
所以不等式组的解集为:,
要使分式有意义,则且,
所以整数,
此时.
②由代数式的值为,得,
此时.
20.解:设该专营店第一个月购进、两种型号手机的数量分别为部和部.
由题意可知:解得:
答:该专营店本次购进、两种型号手机的数分别为部和部;
设第二个月购进型号手机部.
由题意可知:,
解得:,
则不等式的最大整数解为.
答:第二个月最多能购型号手机部
第二课时答案
一、选择题
C.A.C.A.B.B.B.C.C
二、填空题
10..
11.
12.
13.
14.人或人
15.
三、解答题
16.设一只型节能灯的售价是元,一只型节能灯的售价元,
则,
解得:,
答:一只型节能灯的售价是元,一只型节能灯的售价元;
设型节能灯买了只,则型节能灯买了只,共花费元,
依题意,==,
∵ ,
解得:,
∵ 为整数,
∴ 可以取,,,,
方案一、型只,型只,花费元;
方案二、型只,型只,花费元;
方案三、型只,型只,花费元;
方案四、型只,型只,花费元.
17.设购进甲、乙两种商品分别为件、件,
,
解得,,
答:能购进甲、乙两种商品分别为件,件;
设购进甲种商品件,则购进乙种商品件,
,
解得,,
又∵ ,为整数,
∴ =,,,
∴ 该商场共有三种进货方案;
18.
设新建一个地上停车位需万元,新建一个地下停车位需万元,
由题意得:,
解得.
故新建一个地上停车位需万元,新建一个地下停车位需万元;
设新建个地上停车位,
由题意得:,
解得,
因为为整数,所以=或,
对应的=或,
故一共种建造方案;
当=时,投资=(万元),
当=时,投资=(万元),
故当地上建个车位地下建个车位投资最少,金额为万元.
19.设种树苗每棵元,种树苗每棵元,
根据题意,得:,
解得:,
答:种树苗每棵元,种树苗每棵元;
设购进种树苗棵,则购进种树苗棵,
根据题意,得:,
解得:,
所以购买的方案有:
、购进种树苗棵,种树苗棵;
、购进种树苗棵,种树苗棵;
方案一的费用为=元,
方案二的费用为=元,
所以购进种树苗棵,种树苗棵所付工钱最少,最少工钱为元.
第一课时
一、选择题
1.下列选项中是一元一次不等式组的是( )
A. B. C. D.
2.下列说法正确的是( )
A.不等式组的解集是 B.的解集是
C.的解集是= D.的解集是
3.不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
4.若不等式组的解为,则的取值范围是( )
A. B. C. D.
5.已知不等式组的解集为,则值为( )
A. B. C. D.
6.不等式组的解集为,则的取值范围为( )
A. B. C. D.
7.已知关于的不等式组 有个整数解,则符合条件的所有整数的个数为( )
A. B. C. D.
8.设“”,“”,“”分别代表三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,若每个“”的质量为,则“”的质量的取值范围在数轴上表示正确的是
A. B.
C. D.
9.按如图的程序进行操作,规定:程序运行从“输入一个值”到“结果是否”为一次操作.如果必须进行次操作才能得到输出值,那么输入值必须满足( )
A. B. C. D.
10.有一家人参加登山活动,他们要将矿泉水分装在旅行包内带上山,若每人带瓶,则剩余瓶;若每人带瓶,则有一人带了矿泉水,但不足瓶,则这家参加登山的人数为( )
A.人 B.人 C.人 D.人或人
二、填空题
11.不等式组的解集为________.
12.不等式组的整数解为________.
13.若不等式组的解集中只有个整数解,则的取值范围是________.
14.不等式组的最大整数解为________.
15.已知不等式组,是非负整数,则的值为________.
三、解答题
16.解下列不等式(或不等式组),并把解集表示在数轴上:
(1); (2).
17.
(1)解不等式,并把解集在数轴上表示出来.
(2)解不等式组并写出它的所有整数解.
18. 解不等式(组):
(1)解不等式,并把它的解集在数轴上表示出来.
(2)解不等式组,并写出它的所有整数解.
19.已知.
化简;
①若满足不等式组从中选择合适的的整数值代入求的值;
②若代数式的值为,求的值.
20. 某手机专营店代理销售,两种型号手机.手机的进价、售价如下表:
型 号
进 价 元/部 元/部
售 价 元/部 元/部
第一个月:用元购进,两种型号的手机,全部售完后获利元,求第一个月购进,两种型号手机的数量;
第二个月:计划购进,两种型号手机共部,且不超出第一个月购进,两种型号的手机总费用,则型号手机最多能购多少部?
第二课时
一、选择题
1.是不小于的负数,表示为( )
A. B.
C. D.
2.小明要制作一个长方形的相片框架,这个框架的长为,面积不小于,则宽的长度应满足的不等式组为( )
A. B. C. D.
3.将一箱苹果分给若干个小朋友,若每位小朋友分个苹果,则还剩个苹果;若每位小朋友分个苹果,则有-个小朋友分到苹果但不到个苹果.求这一箱苹果的个数与小朋友的人数.若设有人,则可列不等式为( )
A. B.
C. D.
4.小颖同学准备用元买笔和笔记本,已知一支笔元,一本笔记本元,他买了本笔记本,最多还能买多少支笔?设他还能买支笔,则列出的不等式为( )
A. B.
C. D.
5.如图,这是王彬同学设计的一个计算机程序,规定从“输入一个值”到判断“结果是否”为一次运行过程.如果程序运行两次就停止,那么的取值范围是( )
A. B. C. D.
6.有不足个苹果分给若干个小朋友,若每个小朋友分个,则剩个苹果;若每个小朋友分个,则有一个小朋友没分到苹果,且最后一个分到苹果的小朋友分得的苹果数不足个.已知小朋友人数是偶数个,那么苹果的个数是( )
A. B. C. D.
7.有一家人参加登山活动,他们要将矿泉水分装在旅行包内带上山,若每人带瓶,则剩余瓶;若每人带瓶,则有一人带了矿泉水,但不足瓶,则这家参加登山的人数为( )
A.人 B.人 C.人 D.人或人
8.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人盒牛奶,那么剩下盒牛奶;如果分给每位老人盒牛奶,那么最后一位老人分得的牛奶不足盒,但至少盒,则这个敬老院的老人最少有( )
A.人 B.人 C.人 D.人
9.小明去商店购买,两种玩具,共用了元钱,种玩具每件元,种玩具每件元.若每种玩具至少买一件,且种玩具的数量多于种玩具的数量.则小明的购买方案有( )
A.种 B.种 C.种 D.种
二、填空题
10.列不等式组:与的和小于,且与的差是负数________.
11.把一批书分给小朋友,每人本,则余本;每人本,则最后一个小朋友得到书且不足本,则共有小朋友________人.
12.把颗糖平均分成若干份,每份不得少于颗,也不能多于颗,那么一共有________种不同分法.
13.某运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作.如果程序操作进行了两次才停止,那么的取值范围是________.
14.大连某中学七年级网络班级计划将全班同学分成若干小组,开展数学探究活动,若每个小组人,则还余人,若每个小组人,则有一个小组的人数不足人,但多于人,则该班学生的人数是________.
15.若干名学生住宿舍,每间住人,人无处住;每间住人,空一间还有一间不空也不满,问多少学生多少宿舍?设有间宿舍,则可列不等式(组)为________.
三、解答题
16. 学校购进一批节能灯,已知只型节能灯和只型节能灯共需元;只型节能灯和只型节能灯共需元
(1)求一只型节能灯和一只型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共只,并且型节能灯的数量不多于型节能灯数量的倍,不少于型节能灯数量的倍,有几种购买方案,哪种方案最省钱?
17.某商场经销甲、乙两种商品,甲种商品每件进价元,售价元;乙种商品每件进价元,售价元.
(1)若该商场同时购进甲、乙两种商品共件恰好用去元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共件的总利润(利润=售价一进价)不少于元,且甲商品的件数不能低于件,请你帮忙求出该商场有几种进货方案?
18. 某小区准备新建个停车位,以解决小区停车难的问题.已知新建个地上停车位和个地下停车位共需万元;新建个地上停车位和个地下停车位共需万元.
(1)该小区新建个地上停车位和个地下停车位各需多少万元?
(2)若该小区新建车位的投资金额超过万元而不超过万元,问共有几种建造方案?
(3)对(2)中的几种建造方案中,哪一种方案的投资最少?并求出最少投资金额.
19.我市在创建全国文明城市过程中,决定购买,两种树苗对某路段道路进行绿化改造,已知购买种树苗棵,种树苗棵,需要元;若购买种树苗棵,种树苗棵,则需要元.
(1)求购买,两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进种树苗不能少于棵,且用于购买这两种树苗的资金不能超过元,若购进这两种树苗共棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵种树苗可获工钱元,种好一棵种树苗可获工钱元,在第(2)问的各种购买方案中,种好这棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
第一课时答案
一、选择题
D.C.A.A.B.C.A.C.D.B
二、填空题
11.
12.,,
13.
14.
15.
三、解答题
16.(1)
去分母得,,
去括号得,,
移项得,,
合并同类项得,,
把的系数化为得,.
在数轴上表示为:
;
(2),
由①得,,
由②得,,
故不等式组的解集为:.
在数轴上表示为:
.
17.去分母,得:,
去括号,得:,
移项、合并,得:,
将不等式的解集表示在数轴上如下:
由得:,
由得:,
不等式组的解集是,
∴ 所有整数解是,,.
18.去分母,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为,得:,
将解集表示在数轴上如下:
解不等式,得:,
解不等式,得:,
则不等式组的解集为,
所以不等式组的整数解为、、.
19.
解:.
(2)①解得
所以不等式组的解集为:,
要使分式有意义,则且,
所以整数,
此时.
②由代数式的值为,得,
此时.
20.解:设该专营店第一个月购进、两种型号手机的数量分别为部和部.
由题意可知:解得:
答:该专营店本次购进、两种型号手机的数分别为部和部;
设第二个月购进型号手机部.
由题意可知:,
解得:,
则不等式的最大整数解为.
答:第二个月最多能购型号手机部
第二课时答案
一、选择题
C.A.C.A.B.B.B.C.C
二、填空题
10..
11.
12.
13.
14.人或人
15.
三、解答题
16.设一只型节能灯的售价是元,一只型节能灯的售价元,
则,
解得:,
答:一只型节能灯的售价是元,一只型节能灯的售价元;
设型节能灯买了只,则型节能灯买了只,共花费元,
依题意,==,
∵ ,
解得:,
∵ 为整数,
∴ 可以取,,,,
方案一、型只,型只,花费元;
方案二、型只,型只,花费元;
方案三、型只,型只,花费元;
方案四、型只,型只,花费元.
17.设购进甲、乙两种商品分别为件、件,
,
解得,,
答:能购进甲、乙两种商品分别为件,件;
设购进甲种商品件,则购进乙种商品件,
,
解得,,
又∵ ,为整数,
∴ =,,,
∴ 该商场共有三种进货方案;
18.
设新建一个地上停车位需万元,新建一个地下停车位需万元,
由题意得:,
解得.
故新建一个地上停车位需万元,新建一个地下停车位需万元;
设新建个地上停车位,
由题意得:,
解得,
因为为整数,所以=或,
对应的=或,
故一共种建造方案;
当=时,投资=(万元),
当=时,投资=(万元),
故当地上建个车位地下建个车位投资最少,金额为万元.
19.设种树苗每棵元,种树苗每棵元,
根据题意,得:,
解得:,
答:种树苗每棵元,种树苗每棵元;
设购进种树苗棵,则购进种树苗棵,
根据题意,得:,
解得:,
所以购买的方案有:
、购进种树苗棵,种树苗棵;
、购进种树苗棵,种树苗棵;
方案一的费用为=元,
方案二的费用为=元,
所以购进种树苗棵,种树苗棵所付工钱最少,最少工钱为元.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
