浙江版八年级数学下册试题 3.2 中位数和众数-浙教版(含答案)
文档属性
| 名称 | 浙江版八年级数学下册试题 3.2 中位数和众数-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 77.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-10 10:40:59 | ||
图片预览



文档简介
3.2 中位数和众数
一.选择题
1.一组数据5,4,3,6,6的中位数是( )
A.3 B.4 C.5 D.6
2.有一组数据:2,5,3,4,5,3,4,5,则这组数据的众数是( )
A.5 B.4 C.3 D.2
3.一组数据按从小到大排列为2,4,6,x,14,15,若这组数据的中位数为9,则x是( )
A.7 B.9 C.12 D.13
4.某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是( )
读书时间 6小时及以下 7小时 8小时 9小时 10小时及以上
学生人数 6 11 8 8 7
A.8,7 B.8,8 C.8.5,8 D.8.5,7
5.某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如表,则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
锻炼时间/h 5 6 7 8
人数 6 15 10 4
A.6h,6h B.6h,15h C.6.5h,6h D.6.5h,15h
6.在学校的体育训练中,小杰投实心球的7次成绩就如统计图所示,则这7次成绩的中位数和众数分别是( )
A.9.7m,9.8m B.9.7m,9.7m C.9.8m,9.9m D.9.8m,9.8m
7.小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:
步数(万步) 1.0 1.1 1.2 1.3 1.4
天数 3 3 7 5 12
则每天所走的步数这组数据的中位数是( )
A.1.1 B.1.2 C.1.3 D.1.4
8.如果将一组数据5、4、6、5、4、13、5依次重复写10次,会得到70个数组成的一组新数据,关于这组新数据的中位数、众数、平均数,下列说法正确的是( )
A.中位数是4 B.众数是10
C.中位数和众数都是5 D.中位数平均数都是5
9.某款环保电动汽车一次充电后能行里程的统计图如图所示,根据图中信息,这批环保电动汽车一次充电后能行的里程数的中位数和众数分别是( )
A.160千米,165千米 B.160千米,170千米
C.165千米,170千米 D.165千米,165千米
10.一组数据1,2,3,4,4,10.去掉10,剩下的数据与原数据相比,不变的是( )
A.平均数 B.中位数
C.众数 D.平均数和众数
二.填空题
11.已知一组数据为:3,x,6,5,4,若这组数据的众数是4,则x的值为 .
12.一组数据:1,4,4,8,3,10,x,5,5,其平均数是5,则其中位数是 .
13.已知样本1,3,9,a,b的众数是9,平均数是6,则中位数为 .
14.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的众数为 .
15.某校八年级有四个绿化小组,在植树节这天种下数目棵树如下:10,10,x,8,若这组数据的众数和平均数相等,那么x= .
16.已知数据a1,a2,a3,a4,a5的平均数是m,且a1>a2>a3>a4>a5>0,则数据a1,a2,a3,﹣3,a4,a5的平均数和中位数分别是 , .
三.解答题
17.停课不停学,疫情期间,八(1)班30位同学参加运动线上打卡,张老师为了鼓励同学们积极锻炼,统计了这30人15天的打卡次数如表:
打卡次数 7 8 9 14 15
人数 6 9 6 3 6
(1)直接写出打卡次数的众数和中位数;
(2)求所有同学打卡次数的平均数;
(3)为了调动同学们锻炼的积极性,张老师决定制定一个打卡奖励标准,凡打卡次数达到或超过这个标准的同学将获得奖励.请你根据(1)、(2)中所求的统计量,帮助张老师制定一个较为合理的打卡奖励标准,并说明理由.
18.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)甲、乙、丙三家公司在该产品的销售中都声称,其销售的该产品的使用寿命是8年,你如何理解他们的宣传.(请用已学的统计量中加以说明)
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
(3)如果你是丙公司的推销员,你将如何结合上述数据,对本公司的产品进行推销?
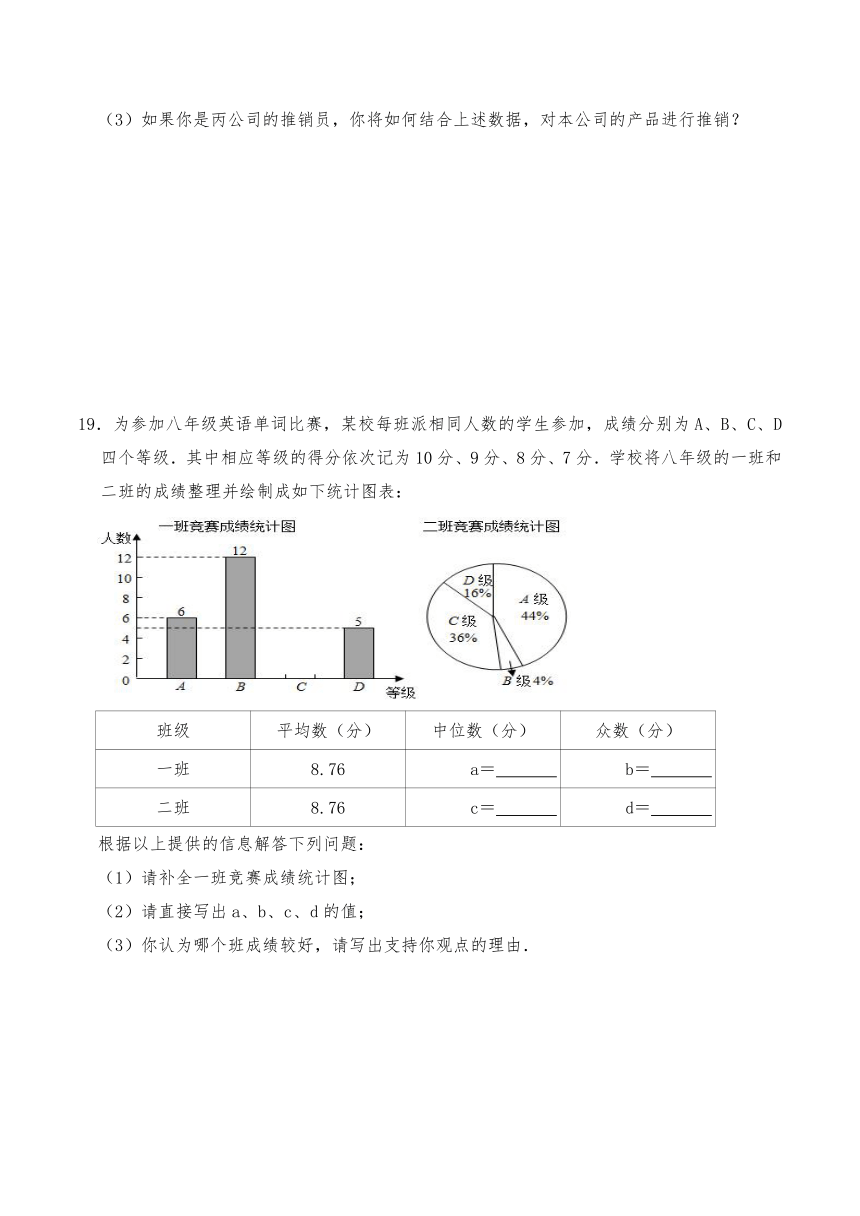
19.为参加八年级英语单词比赛,某校每班派相同人数的学生参加,成绩分别为A、B、C、D四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.学校将八年级的一班和二班的成绩整理并绘制成如下统计图表:
班级 平均数(分) 中位数(分) 众数(分)
一班 8.76 a= b=
二班 8.76 c= d=
根据以上提供的信息解答下列问题:
(1)请补全一班竞赛成绩统计图;
(2)请直接写出a、b、c、d的值;
(3)你认为哪个班成绩较好,请写出支持你观点的理由.
20.在学校组织的“学习强国”知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长张老师将801班和802班的成绩进行整理并绘制成如下的统计图
(1)在本次竞赛中,802班C级的人数有多少?
(2)请你将下面的表格补充完整:
成绩 班级 平均数(分) 中位数(分) 众数(分) B级及以上人数
801班 87.6 90 18
802班 87.6 100
(3)结合以上统计量,请你从不同角度对这次竞赛成绩的结果进行分析(写出两条).
答案
一.选择题
C.A.C.A.A.B.C.C.D.C.
二.填空题
11.4.
12.5.
13.8.
14.8.
15.12.
16.,,
三.解答题
17.解:(1)8次的人数最多,众数为8次;
共30人,所有同学打卡次数从小到大排列第15个、第16个数反比为8次,9次,
中位数为(8+9)÷2=8.5(次);
(2)平均数为(7×6+8×9+9×6+14×3+15×6)÷30=10(次);
(3)为了调动同学们锻炼的积极性,打卡奖励标准可以定为所有同学打卡次数的中位数.
因为共有30人,9次以上(含9次)的有15人,等于总数的一半.
18.解:(1)甲厂:平均数为(4+5+5+5+5+7+9+12+13+15)=8,众数为5,中位数为6;
乙厂:平均数为(6+6+8+8+8+9+10+12+14+15)=9.6,众数为8,中位数为8.5;
丙厂:平均数为(4+4+4+6+7+9+13+15+16+16)=9.4,众数为4,中位数为8;
∴甲公司用的是平均数;乙公司用的是众数;丙公司用的是中位数.
(2)乙公司.因为从平均数、众数和中位数三项指标上看,都比其他的两个公司要好,
他们的产品质量更高.
(3)①丙公司的平均数和中位数都比甲公司高;②以从产品寿命的最高年限考虑购买丙公司的产品的使用寿命比较高的机会比乙公司产品大一些.
19.解:(1)设一班C等级的人数为x,
则8.76(6+12+x+5)=6×10+9×12+8x+5×7,
解得:x=2,
补全一班竞赛成绩统计图如图所示:
(2)a=9; b=9; c=8; d=10,
故答案为:9,9,8,10.
(3)一班的平均分和二班的平均分都为8.76分,两班平均成绩都一样;一班的中位数9分大于二班的中位数8分,一班成绩比二班好.
综上,一班成绩比二班好.
20.解:(1)801班人数有:6+12+2+5=25(人),
∵每班参加比赛的人数相同,
∴802班有25人,
∴C级的人数=25×36%=9(人),
(2)801班成绩的众数为90分,
802班A级学生=25×44%=11,
B级学生=25×4%=1,
C级学生=25×36%=9,
D级学生=25×16%=4,
802班中位数为C级学生,即80分,
802班B级及以上人数为11+1=12(人),
补全表格如下:
平均数(分) 中位数(分) 众数(分) B级及以上人数
901班 87.6 90 90 18
902班 87.6 80 100 12
(3)①从平均数的角度看两班成绩一样;从中位数的角度看801班比802班的成绩好;所以801班成绩好.
②从平均数的角度看两班成绩一样,从众数的角度看982班比801班的成绩好,所以802班成绩好.(答案不唯一)
一.选择题
1.一组数据5,4,3,6,6的中位数是( )
A.3 B.4 C.5 D.6
2.有一组数据:2,5,3,4,5,3,4,5,则这组数据的众数是( )
A.5 B.4 C.3 D.2
3.一组数据按从小到大排列为2,4,6,x,14,15,若这组数据的中位数为9,则x是( )
A.7 B.9 C.12 D.13
4.某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是( )
读书时间 6小时及以下 7小时 8小时 9小时 10小时及以上
学生人数 6 11 8 8 7
A.8,7 B.8,8 C.8.5,8 D.8.5,7
5.某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如表,则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
锻炼时间/h 5 6 7 8
人数 6 15 10 4
A.6h,6h B.6h,15h C.6.5h,6h D.6.5h,15h
6.在学校的体育训练中,小杰投实心球的7次成绩就如统计图所示,则这7次成绩的中位数和众数分别是( )
A.9.7m,9.8m B.9.7m,9.7m C.9.8m,9.9m D.9.8m,9.8m
7.小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:
步数(万步) 1.0 1.1 1.2 1.3 1.4
天数 3 3 7 5 12
则每天所走的步数这组数据的中位数是( )
A.1.1 B.1.2 C.1.3 D.1.4
8.如果将一组数据5、4、6、5、4、13、5依次重复写10次,会得到70个数组成的一组新数据,关于这组新数据的中位数、众数、平均数,下列说法正确的是( )
A.中位数是4 B.众数是10
C.中位数和众数都是5 D.中位数平均数都是5
9.某款环保电动汽车一次充电后能行里程的统计图如图所示,根据图中信息,这批环保电动汽车一次充电后能行的里程数的中位数和众数分别是( )
A.160千米,165千米 B.160千米,170千米
C.165千米,170千米 D.165千米,165千米
10.一组数据1,2,3,4,4,10.去掉10,剩下的数据与原数据相比,不变的是( )
A.平均数 B.中位数
C.众数 D.平均数和众数
二.填空题
11.已知一组数据为:3,x,6,5,4,若这组数据的众数是4,则x的值为 .
12.一组数据:1,4,4,8,3,10,x,5,5,其平均数是5,则其中位数是 .
13.已知样本1,3,9,a,b的众数是9,平均数是6,则中位数为 .
14.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的众数为 .
15.某校八年级有四个绿化小组,在植树节这天种下数目棵树如下:10,10,x,8,若这组数据的众数和平均数相等,那么x= .
16.已知数据a1,a2,a3,a4,a5的平均数是m,且a1>a2>a3>a4>a5>0,则数据a1,a2,a3,﹣3,a4,a5的平均数和中位数分别是 , .
三.解答题
17.停课不停学,疫情期间,八(1)班30位同学参加运动线上打卡,张老师为了鼓励同学们积极锻炼,统计了这30人15天的打卡次数如表:
打卡次数 7 8 9 14 15
人数 6 9 6 3 6
(1)直接写出打卡次数的众数和中位数;
(2)求所有同学打卡次数的平均数;
(3)为了调动同学们锻炼的积极性,张老师决定制定一个打卡奖励标准,凡打卡次数达到或超过这个标准的同学将获得奖励.请你根据(1)、(2)中所求的统计量,帮助张老师制定一个较为合理的打卡奖励标准,并说明理由.
18.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)甲、乙、丙三家公司在该产品的销售中都声称,其销售的该产品的使用寿命是8年,你如何理解他们的宣传.(请用已学的统计量中加以说明)
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
(3)如果你是丙公司的推销员,你将如何结合上述数据,对本公司的产品进行推销?
19.为参加八年级英语单词比赛,某校每班派相同人数的学生参加,成绩分别为A、B、C、D四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.学校将八年级的一班和二班的成绩整理并绘制成如下统计图表:
班级 平均数(分) 中位数(分) 众数(分)
一班 8.76 a= b=
二班 8.76 c= d=
根据以上提供的信息解答下列问题:
(1)请补全一班竞赛成绩统计图;
(2)请直接写出a、b、c、d的值;
(3)你认为哪个班成绩较好,请写出支持你观点的理由.
20.在学校组织的“学习强国”知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长张老师将801班和802班的成绩进行整理并绘制成如下的统计图
(1)在本次竞赛中,802班C级的人数有多少?
(2)请你将下面的表格补充完整:
成绩 班级 平均数(分) 中位数(分) 众数(分) B级及以上人数
801班 87.6 90 18
802班 87.6 100
(3)结合以上统计量,请你从不同角度对这次竞赛成绩的结果进行分析(写出两条).
答案
一.选择题
C.A.C.A.A.B.C.C.D.C.
二.填空题
11.4.
12.5.
13.8.
14.8.
15.12.
16.,,
三.解答题
17.解:(1)8次的人数最多,众数为8次;
共30人,所有同学打卡次数从小到大排列第15个、第16个数反比为8次,9次,
中位数为(8+9)÷2=8.5(次);
(2)平均数为(7×6+8×9+9×6+14×3+15×6)÷30=10(次);
(3)为了调动同学们锻炼的积极性,打卡奖励标准可以定为所有同学打卡次数的中位数.
因为共有30人,9次以上(含9次)的有15人,等于总数的一半.
18.解:(1)甲厂:平均数为(4+5+5+5+5+7+9+12+13+15)=8,众数为5,中位数为6;
乙厂:平均数为(6+6+8+8+8+9+10+12+14+15)=9.6,众数为8,中位数为8.5;
丙厂:平均数为(4+4+4+6+7+9+13+15+16+16)=9.4,众数为4,中位数为8;
∴甲公司用的是平均数;乙公司用的是众数;丙公司用的是中位数.
(2)乙公司.因为从平均数、众数和中位数三项指标上看,都比其他的两个公司要好,
他们的产品质量更高.
(3)①丙公司的平均数和中位数都比甲公司高;②以从产品寿命的最高年限考虑购买丙公司的产品的使用寿命比较高的机会比乙公司产品大一些.
19.解:(1)设一班C等级的人数为x,
则8.76(6+12+x+5)=6×10+9×12+8x+5×7,
解得:x=2,
补全一班竞赛成绩统计图如图所示:
(2)a=9; b=9; c=8; d=10,
故答案为:9,9,8,10.
(3)一班的平均分和二班的平均分都为8.76分,两班平均成绩都一样;一班的中位数9分大于二班的中位数8分,一班成绩比二班好.
综上,一班成绩比二班好.
20.解:(1)801班人数有:6+12+2+5=25(人),
∵每班参加比赛的人数相同,
∴802班有25人,
∴C级的人数=25×36%=9(人),
(2)801班成绩的众数为90分,
802班A级学生=25×44%=11,
B级学生=25×4%=1,
C级学生=25×36%=9,
D级学生=25×16%=4,
802班中位数为C级学生,即80分,
802班B级及以上人数为11+1=12(人),
补全表格如下:
平均数(分) 中位数(分) 众数(分) B级及以上人数
901班 87.6 90 90 18
902班 87.6 80 100 12
(3)①从平均数的角度看两班成绩一样;从中位数的角度看801班比802班的成绩好;所以801班成绩好.
②从平均数的角度看两班成绩一样,从众数的角度看982班比801班的成绩好,所以802班成绩好.(答案不唯一)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
