浙教版八年级数学上册试题 1.3 证明同步练习(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 1.3 证明同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 115.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 01:11:07 | ||
图片预览


文档简介
1.3 证明
一、选择题
1.若等腰三角形的一个外角是,则这个等腰三角形底角的度数为( )
A. B. C.或 D.或
2.已知三角形的三个外角之比为,则此三角形为( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.直角三角形
3.如图,在中,是延长线上一点,,,则( )
A. B. C. D.
4.将一副三角板按图中方式叠放,则等于
A. B. C. D.
5.将一副三角板按图中方式叠放,则的度数为( )
A. B. C. D.
6.如图,,,的大小关系为( )
A. B. C. D.
7.如果三角形的一个外角与它不相邻的两个内角的和为,那么与这个外角相邻的内角等于( )
A. B. C. D.
8.如图所示,已知为直角三角形,,若沿图中虚线剪去,则等于
A. B. C. D.
二、填空题
9.在中,已知,,则的外角的度数是________.
10.某一个三角形的外角中有一个角是锐角,那么这个三角形是________角三角形.
11.如图,=,=,则的度数是________.
12.一副分别含有和角的两个直角三角板,拼成如上图形,则=________度.
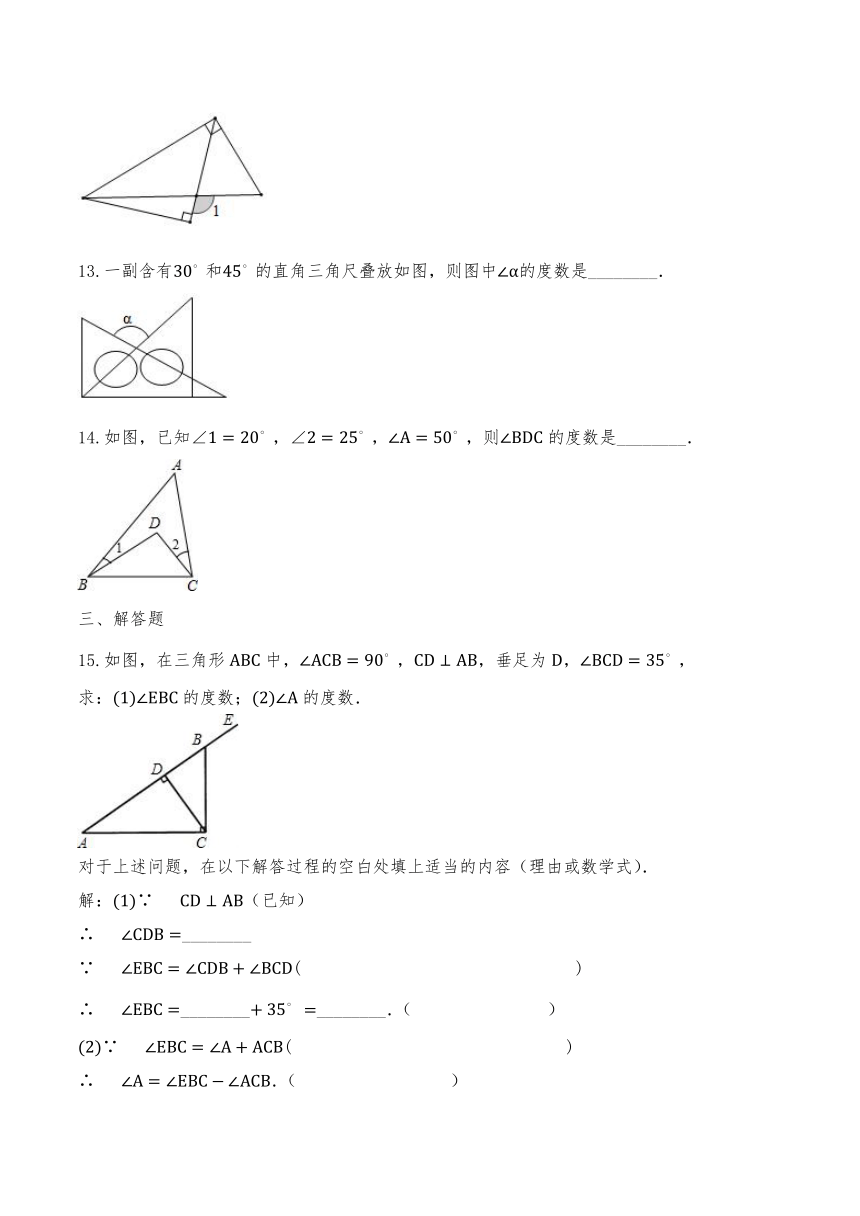
13.一副含有和的直角三角尺叠放如图,则图中的度数是________.
14.如图,已知,,,则的度数是________.
三、解答题
15.如图,在三角形中,,,垂足为,,
求:的度数;的度数.
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:∵ (已知)
∴ ________
∵ ( )
∴ ________________.( )
∵ ( )
∴ .( )
∵ ( )
∴ ________.( )
16.已知:如图,在中,=,平分外角.求证:.
17.如图,是的外角的平分线,且交的延长线于点,证明:=.
18.如图所示.=,=,=,=,=.求的度数.
答案
一、选择题
C.D.B.B.D.A.C.C
二、填空题
9.
10.钝
11.
12.
13.
14.
三、解答题
15.
解:∵ ,(已知)
∴ ,
∵ ,(三角形的外角等于与它不相邻两个内角的和)
∴ .(等量代换)
∵ ,(三角形的外角等于与它不相邻的两个内角的和)
∴ .(等式的性质)
∵ ,(已知)
∴ .(等量代换)
16.证明:由三角形的外角性质得,=,
∵ =,
∴ =,
∵ 平分外角,
∴ =,
∴ =,
∴ .
17.
证明:∵ 平分,
∴ =,
∵ =,
∴ =,
∵ =,
∴ ==.
18.
∵ =,=,
∴ ==,
∵ =,
∴ ==,
∴ ==,
∵ =,
∴ =,
∴ ===,
∵ =,
∴ =,
∴ ===,
∴ ===,
∵ =,
∴ =,
∴ ===.
一、选择题
1.若等腰三角形的一个外角是,则这个等腰三角形底角的度数为( )
A. B. C.或 D.或
2.已知三角形的三个外角之比为,则此三角形为( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.直角三角形
3.如图,在中,是延长线上一点,,,则( )
A. B. C. D.
4.将一副三角板按图中方式叠放,则等于
A. B. C. D.
5.将一副三角板按图中方式叠放,则的度数为( )
A. B. C. D.
6.如图,,,的大小关系为( )
A. B. C. D.
7.如果三角形的一个外角与它不相邻的两个内角的和为,那么与这个外角相邻的内角等于( )
A. B. C. D.
8.如图所示,已知为直角三角形,,若沿图中虚线剪去,则等于
A. B. C. D.
二、填空题
9.在中,已知,,则的外角的度数是________.
10.某一个三角形的外角中有一个角是锐角,那么这个三角形是________角三角形.
11.如图,=,=,则的度数是________.
12.一副分别含有和角的两个直角三角板,拼成如上图形,则=________度.
13.一副含有和的直角三角尺叠放如图,则图中的度数是________.
14.如图,已知,,,则的度数是________.
三、解答题
15.如图,在三角形中,,,垂足为,,
求:的度数;的度数.
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:∵ (已知)
∴ ________
∵ ( )
∴ ________________.( )
∵ ( )
∴ .( )
∵ ( )
∴ ________.( )
16.已知:如图,在中,=,平分外角.求证:.
17.如图,是的外角的平分线,且交的延长线于点,证明:=.
18.如图所示.=,=,=,=,=.求的度数.
答案
一、选择题
C.D.B.B.D.A.C.C
二、填空题
9.
10.钝
11.
12.
13.
14.
三、解答题
15.
解:∵ ,(已知)
∴ ,
∵ ,(三角形的外角等于与它不相邻两个内角的和)
∴ .(等量代换)
∵ ,(三角形的外角等于与它不相邻的两个内角的和)
∴ .(等式的性质)
∵ ,(已知)
∴ .(等量代换)
16.证明:由三角形的外角性质得,=,
∵ =,
∴ =,
∵ 平分外角,
∴ =,
∴ =,
∴ .
17.
证明:∵ 平分,
∴ =,
∵ =,
∴ =,
∵ =,
∴ ==.
18.
∵ =,=,
∴ ==,
∵ =,
∴ ==,
∴ ==,
∵ =,
∴ =,
∴ ===,
∵ =,
∴ =,
∴ ===,
∴ ===,
∵ =,
∴ =,
∴ ===.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
