4.5 相似三角形的性质及应用同步练习(无答案)2023-2024学年浙教版九年级数学上册
文档属性
| 名称 | 4.5 相似三角形的性质及应用同步练习(无答案)2023-2024学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 204.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 11:20:48 | ||
图片预览


文档简介
浙教版九年级上册4.5 相似三角形的性质及应用
一、选择题
1.如图,中,,,D为BC上一点,,的面积为a,则的面积为( )
A . a B . C . D .
2.如图 ,经相似变换后得到 ,已知 , , , ,求 的长( )
A . 10 B . 3 C . 8 D .
3.如图,在 ABC中,DE∥BC,AD=5,AB=12,AE=3,则AC的长是( )
A . B . C . 20 D . 15
4.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半.若BC=,则△ABC移动的距离是( ).
A . B . C . D .
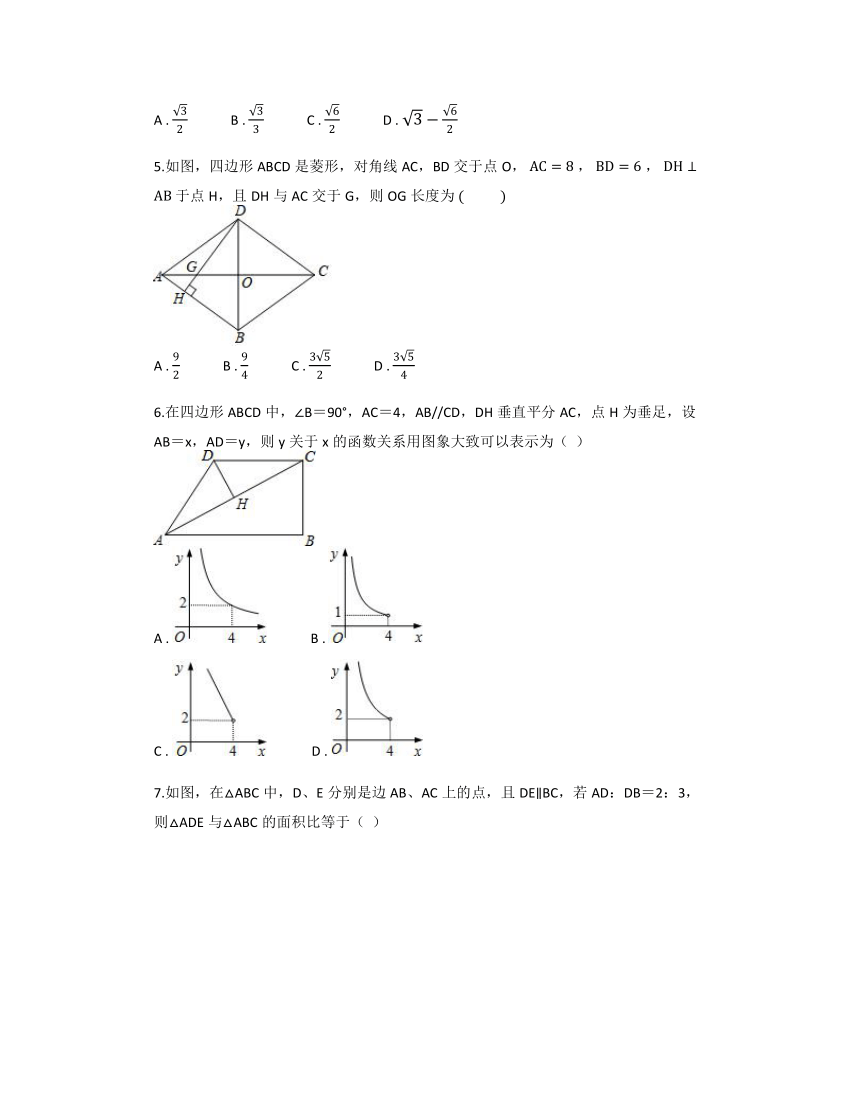
5.如图,四边形ABCD是菱形,对角线AC,BD交于点O, , , 于点H,且DH与AC交于G,则OG长度为
A . B . C . D .
6.在四边形ABCD中,∠B=90°,AC=4,AB//CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A . B .
C . D .
7.如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若AD:DB=2:3,则△ADE与△ABC的面积比等于( )
A . 2:3 B . 4:5 C . 4:9 D . 4:25
8.如图,在□ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则△DEF与四边形EFCO的面积比为( )
A . 1: 4 B . 1:5 C . 1:6 D . 1: 7
9.如图,在矩形 中, , , 是 边上一动点(不含端点 ),连接 , 是 边上一点,设 ,若存在唯一点 ,使 ,则 的值是( )
A . B . C . 3 D . 6
10.如图,在△ABC中,以BC为直径的圆分别交边AC,AB于D,E两点,连结BD,DE。若BD平分∠ABC,则下列结论不一定成立的是( )
A . BD⊥AC B . C . △ADE是等腰三角形 D . BC=2AD
11.如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中错误的是( )
A . B . C . △ADE∽△ABC D .
12. 两块完全相同的含30°角的直角三角板ABC和A'B'C′重合在一起,将三角板A'B'C'绕直角顶点C'按逆时针方向旋转α(0°<α≤90°),如图所示.以下结论错误的是( )
A . 当α=30°时,A'C与AB的交点恰好为AB中点 B . 当α=60°时,A'B'恰好经过点B C . 在旋转过程中,存在某一时刻,使得AA'=BB' D . 在旋转过程中,始终存在AA'⊥BB'
二、填空题
13.如图,AB和DE是直立在地面上的两根立柱,AB=4m,AB在阳光下的影长BC=3m,在同一时刻阳光下DE的影长EF=4m,则DE的长为 _____米.
14.如图,矩形ABCD的对角线AC、BD交于点O,点E是BC边上的一动点,连结OE,将 BOC分成了两个三角形,若BE=OB,且 ,则∠BOC的度数为_____.
15.在“测量学校教学楼的高度”的数学活动中,小刚同学使用镜面反射法进行测量,如图所示.若 米, 米, 米,则这个学校教学楼的高度为_____米.
16.如图,一组平行线L1、L2、L3截两相交直线L4、L5,则 _____.
三、解答题
17.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.
18.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的边PN∶PQ=1∶2,则这个矩形的长、宽各是多少?
19.为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
20.如图,大刚在晚上由灯柱A走向灯柱B,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱A的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱B的底部,已知大刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求:两根灯柱之间的距离.
21.在中,已知是BC边的中点,点是的重心,过点的直线分别交AB,AC于点E,F.
(1)如图甲所示,当时,求证:.
(2)如图乙所示,当EF和BC不平行,且点E,F分别在线段AB,AC上时,第(1)题中的结论是否成立 如果成立,请给出证明;如果不成立,请说明理由.
一、选择题
1.如图,中,,,D为BC上一点,,的面积为a,则的面积为( )
A . a B . C . D .
2.如图 ,经相似变换后得到 ,已知 , , , ,求 的长( )
A . 10 B . 3 C . 8 D .
3.如图,在 ABC中,DE∥BC,AD=5,AB=12,AE=3,则AC的长是( )
A . B . C . 20 D . 15
4.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半.若BC=,则△ABC移动的距离是( ).
A . B . C . D .
5.如图,四边形ABCD是菱形,对角线AC,BD交于点O, , , 于点H,且DH与AC交于G,则OG长度为
A . B . C . D .
6.在四边形ABCD中,∠B=90°,AC=4,AB//CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A . B .
C . D .
7.如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若AD:DB=2:3,则△ADE与△ABC的面积比等于( )
A . 2:3 B . 4:5 C . 4:9 D . 4:25
8.如图,在□ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则△DEF与四边形EFCO的面积比为( )
A . 1: 4 B . 1:5 C . 1:6 D . 1: 7
9.如图,在矩形 中, , , 是 边上一动点(不含端点 ),连接 , 是 边上一点,设 ,若存在唯一点 ,使 ,则 的值是( )
A . B . C . 3 D . 6
10.如图,在△ABC中,以BC为直径的圆分别交边AC,AB于D,E两点,连结BD,DE。若BD平分∠ABC,则下列结论不一定成立的是( )
A . BD⊥AC B . C . △ADE是等腰三角形 D . BC=2AD
11.如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中错误的是( )
A . B . C . △ADE∽△ABC D .
12. 两块完全相同的含30°角的直角三角板ABC和A'B'C′重合在一起,将三角板A'B'C'绕直角顶点C'按逆时针方向旋转α(0°<α≤90°),如图所示.以下结论错误的是( )
A . 当α=30°时,A'C与AB的交点恰好为AB中点 B . 当α=60°时,A'B'恰好经过点B C . 在旋转过程中,存在某一时刻,使得AA'=BB' D . 在旋转过程中,始终存在AA'⊥BB'
二、填空题
13.如图,AB和DE是直立在地面上的两根立柱,AB=4m,AB在阳光下的影长BC=3m,在同一时刻阳光下DE的影长EF=4m,则DE的长为 _____米.
14.如图,矩形ABCD的对角线AC、BD交于点O,点E是BC边上的一动点,连结OE,将 BOC分成了两个三角形,若BE=OB,且 ,则∠BOC的度数为_____.
15.在“测量学校教学楼的高度”的数学活动中,小刚同学使用镜面反射法进行测量,如图所示.若 米, 米, 米,则这个学校教学楼的高度为_____米.
16.如图,一组平行线L1、L2、L3截两相交直线L4、L5,则 _____.
三、解答题
17.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.
18.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的边PN∶PQ=1∶2,则这个矩形的长、宽各是多少?
19.为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
20.如图,大刚在晚上由灯柱A走向灯柱B,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱A的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱B的底部,已知大刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求:两根灯柱之间的距离.
21.在中,已知是BC边的中点,点是的重心,过点的直线分别交AB,AC于点E,F.
(1)如图甲所示,当时,求证:.
(2)如图乙所示,当EF和BC不平行,且点E,F分别在线段AB,AC上时,第(1)题中的结论是否成立 如果成立,请给出证明;如果不成立,请说明理由.
同课章节目录
