圆的基本性质
图片预览







文档简介
课件57张PPT。初三数学
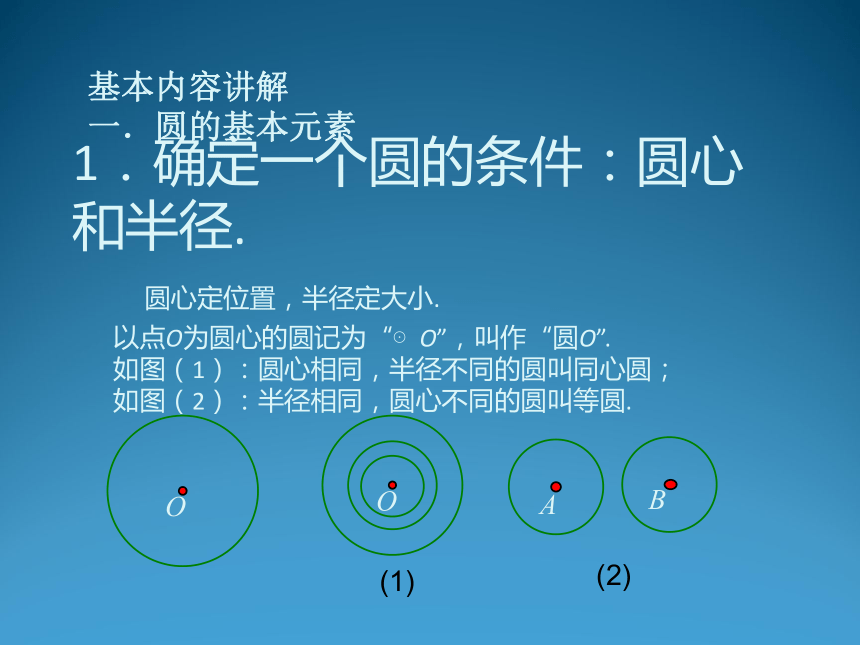
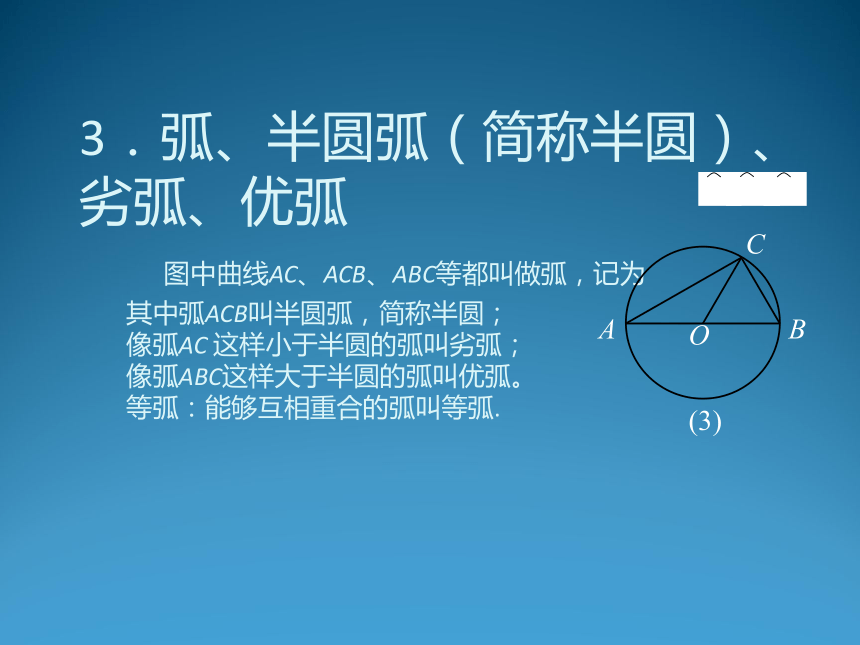
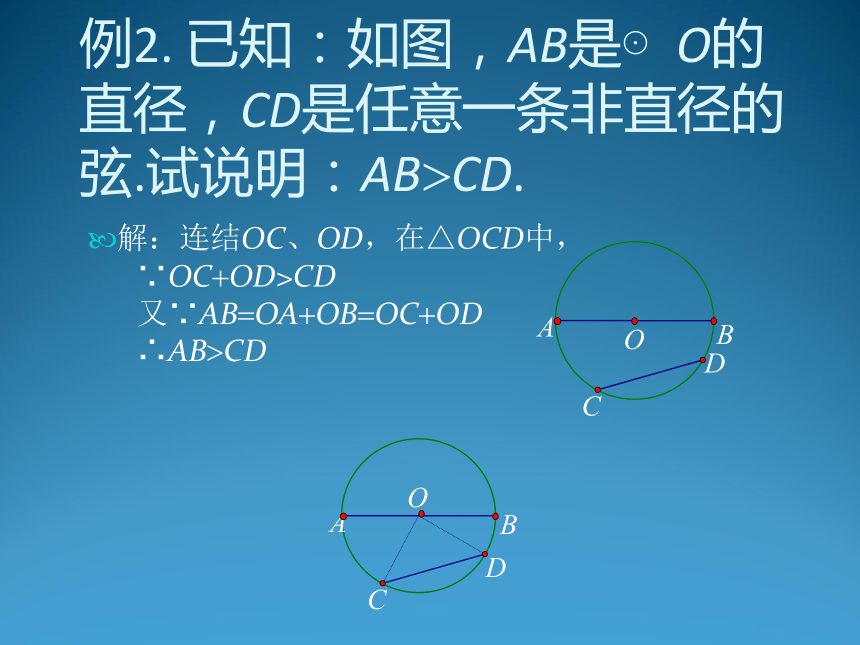
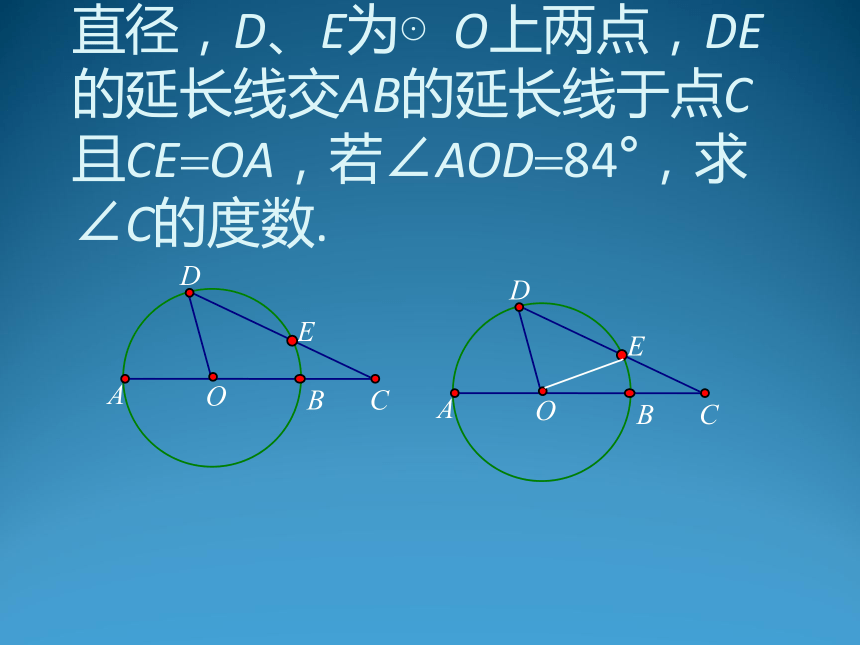
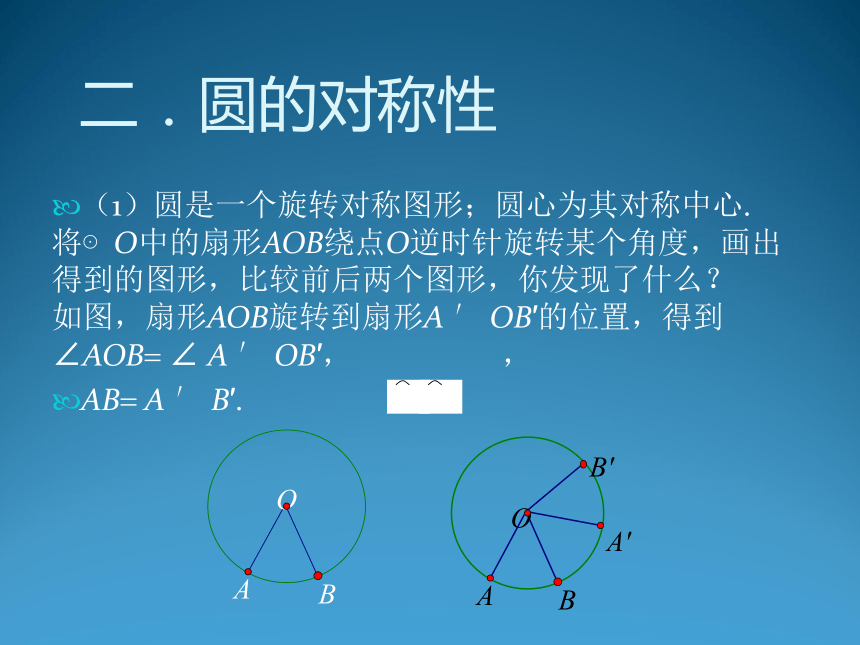
圆的认识 圆的基本元素. 圆的对称性. 圆周角. 1.确定一个圆的条件:圆心和半径. 圆心定位置,半径定大小. 以点O为圆心的圆记为“⊙O”,叫作“圆O”. 如图(1):圆心相同,半径不同的圆叫同心圆; 如图(2):半径相同,圆心不同的圆叫等圆. 基本内容讲解 一.圆的基本元素2.弦、直径、半径 (3) 线段AB、AC、BC都是连结圆上两点的线段,这样的线段叫圆的弦;其中弦AB经过圆心,叫圆的直径;而线段OA、OB、OC都是连结圆心和圆上一点的线段,叫圆的半径。 同圆或等圆中,半径都相等; 3.弧、半圆弧(简称半圆)、劣弧、优弧 图中曲线AC、ACB、ABC等都叫做弧,记为 其中弧ACB叫半圆弧,简称半圆; 像弧AC 这样小于半圆的弧叫劣弧; 像弧ABC这样大于半圆的弧叫优弧。 等弧:能够互相重合的弧叫等弧. 4.圆心角 图中,∠AOC、∠BOC都是圆心角。 例1. 下列说法中正确的是( ) ①直径是弦; ②弦是直径; ③半圆是弧,但弧不一定是半圆; ④半径相等的两个半圆是等弧; ⑤长度相等的两条弧是等弧. A.①④ B.①③④ C.①③④⑤ D.①②③④⑤ 解:选B. 例2. 已知:如图,AB是⊙O的直径,CD是任意一条非直径的弦.试说明:AB?CD. 解:连结OC、OD,在△OCD中, ∵OC?OD>CD 又∵AB?OA?OB?OC?OD ∴AB?CD ? 例3. 已知:如图,AB是⊙O的直径,D、E为⊙O上两点,DE的延长线交AB的延长线于点C且CE?OA,若∠AOD?84°,求∠C的度数. 解:连结OE ∵CE?OA,OA?OD?OE ∴∠D?∠OED?2∠C ∵∠AOD?∠D? ∠C ∴∠AOD?3∠C ∵∠AOD?84° ∴∠C?28° 二.圆的对称性 (1)圆是一个旋转对称图形;圆心为其对称中心. 将⊙O中的扇形AOB绕点O逆时针旋转某个角度,画出得到的图形,比较前后两个图形,你发现了什么? 如图,扇形AOB旋转到扇形A ′ OB′的位置,得到 ∠AOB? ∠ A ′ OB′, ,
AB? A ′ B′. ①在一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.
②在一个圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等.
③在一个圆中,如果弦相等,那么它所对的圆心角相等,圆心角所对的弧相等.
上面这三个结论,简称“三量关系”。 例4 如图,在⊙O中, ,∠A?40°, 求∠C的度数. 解:∵ ∴AB?AC ∴∠B?∠C ∵∠A?40° ∴∠C?∠B? 70° ? (2)圆是一个轴对称图形,任意一条直径所在的 直线都是它的对称轴. 如图,在圆形纸片上任意画一条垂直于直径 CD的弦AB,垂足为P,再将纸片沿直径CD 对折,比较AP与BP, 你能发现什么? 得到:AP?BP, ∵AB⊥直径CD于P ∴AP?BP,
这个结论也称“垂径定理”. 例5. 已知:如图,半径为6的⊙O中,弦AB垂直 平分半径OC,求弦AB的长. 解:连结OA,设AB交OC于点E ∵弦AB垂直平分半径OC ∴ , AE?BE ∵⊙O的半径为6 ∴OA?6,OE?3 在Rt△OAE中,
∴AB? ∴弦AB的长为 . 例6.半径为5的⊙O中,弦AB? 6cm,弦CD? 8cm.且AB?? CD,求AB与CD之间的距离. 解:如图(1),连结OA、OC 过O作MN⊥AB于M,交CD于N, ∵AB?? CD ∴MN⊥CD于N ∴AM?MB,CN?ND ∵AB? 6,CD? 8 ∴AM? 3,CN? 4 又∵半径为5 ∴OA?OC? 5 ∴在Rt△AOM及Rt△CON中,
∴MN?OM? ON?4? 3=7 如图(2),同理可得MN?OM?ON?4?3? 1 ∴AB与CD之间的距离是7cm或1cm. (1)(2)(3)(4)(5)三. 圆周角 如图,图(2)所示的角为圆周角. (1)半圆或直径所对的圆周角都相等,都等于90°(直角). (2)90°的圆周角所对的弦是圆的直径(所对的弧是半圆). (3)一条弧所对的圆周角等于该弧所对的圆心角的一半. (4)在同圆或等圆中,同弧或等弧所对的圆周角相等,都 等于该弧所对的圆心角的一半;相等的圆 周角所对的弧相等.例7. 已知:如图,AB是⊙O的直径,AC、AD为 弦,且AD平分∠BAC,若AB?10,AC? 6, 求AD的长. 解:连结BD并延长交AC的延长线于点E,连结BC ∵AB是⊙O的直径 ∴∠ACB?∠ADB?90° ∴BC⊥AE,AD⊥BE 又∵AD平分∠BAC ∴AE?AB,DE?BD ∵AB? 10,AC? 6 ∴CE? AE?AC? 4 , 在Rt△ABC中
在Rt△BCE中,
∴ 在Rt△ABD中,
∴AD? 例8.?? 如图,AB是⊙O的直径,C为⊙O上一点,AD为弦,DE⊥AB于F交AC于E,试问AD2与AE·AC是否相等?为什么? 分析:解:AD2与AE·AC相等。 延长DE交⊙O于H ∵DE⊥AB ,AB是⊙O的直径 ∴ ∴∠ADH? ∠C 又∵∠DAE? ∠CAD ∴△ADE∽△ACD ∴ ∴AD2? AE·AC
另解:连结BD ∵AB是⊙O的直径 ∴∠ADB? 90°
又∵DE⊥AB ∴∠ADE? ∠B ∵∠C? ∠B ∴∠ADE? ∠C 又∵∠DAE? ∠CAD ∴△ADE∽△ACD ∴ ∴AD2? AE·AC 例9.?? 如图,AB为半圆O的直径,弦AD、BC交于点P,CD? 4,AB? 5,求cos∠BPD的值. 分析:解:连结BD ∵AB为半圆O的直径 ∴∠ADB? 90° 在△BPD中,cos∠BPD? ∵∠C? ∠A,∠CDP? ∠PBA ∴△CDP∽△ABP ∴ ∴cos∠BPD? ∵CD? 4,AB? 5 cos∠BPD? ? 小结 1. 与圆有关的概念:确定一个圆的条件是 圆心 和半径. 了解圆中的基本概念:弦、直径、半径、弧、半圆弧(简称半圆)、劣弧、优弧、等弧。注意只有能够互相重合的弧叫等弧. 2.由圆的旋转对称性得到圆心角、弧、弦
“三量关系” ①在一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等. ②在一个圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等. ③在一个圆中,如果弦相等,那么它所对的圆心角相等,圆心角所对的弧相等. 由圆的轴对称性得到“垂径定理”。也就是说,由直径垂直于弦可以得到三个平分,由直径CD垂直于弦AB于点P,可以得到AP? BP, ? 3.圆心角及圆周角的有关结论: (1)半圆或直径所对的圆周角都相等,都等于90°(直角). (2)90°的圆周角所对的弦是圆的直径(所对的弧是半圆). (3)一条弧所对的圆周角等于该弧所对的圆心角的一半. (4)在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等. 课后练习 1.下列说法中正确的是( ) ①??? 过圆心的线段是直径; ②直径相等的两个圆是等圆; ③小于半圆的弧是优弧; ④一条弦把圆分成两条弧,这两条弧不可能是等弧. A.①②④ B.①④ C.②④ D.②2.已知:如图,AB是⊙O的直径,CD是弦,AB、CD的延长线交于点E,若AB=2DE,∠E=18°,则∠AOC的度数是( ). A.72° B.60° C.54° D.36° 3.如图,AB是⊙O的直径,AC是弦,OD∥BC交AC于D,BC=16,则OD的长是( ). A.12 B.10 C.8 D.6 4.下列结论中:①长度相等的弧所对的圆心角相等;②相等的圆心角所对的弧相等;③同一个圆中,相等的弦所对的弧相等;④若直径垂直于圆的一条弦,则直径平分弦所对的两条弧.其中正确的个数是( ) A.0个 B.1个 C.2个 D.3个 5.如图,⊙O中,∠AOB=2∠COD,则弦AB与2CD的大小关系是( ) A.AB>2CD B.AB=2CD C.AB<2CD D.AB与2CD的大小关系不确定? 6.⊙O中弦AB与直径CD相交成30°,交点为P,且分CD为2和10两段,则弦AB的长度为( ) A.2 B.4 C. D. 7.⊙O中弦AB把圆分成1:3两部分,则圆周角∠ACB的度数为( ) A.45° B.135° C.45°或135° D.以上答案都不对 ? ? ? 8.如图,圆中相等的圆周角的对数和相似三角形的对数分别是( ) A.4,2 B.4,6 C.6,6 D.2,2 9.等腰三角形ABC中,顶角∠BAC=70°,以AB为直径的半圆交BC于点D,则∠BAD的度数为( ) A.55° B.35° C.70° D.90° ? ? ? 10.如图,A、B、C三点都在⊙O上,AD⊥BC于D,⊙O的直径AE交BC边于点G,有四个结论:①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AG;④AG·EG=BG·CG.其中正确的个数是( ) A.1个 B.2个 C.3个 D.4个 练习解答 1.下列说法中正确的是( ) ①过圆心的线段是直径; ②直径相等的两个圆是等圆; ③小于半圆的弧是优弧; ④一条弦把圆分成两条弧,这两条弧不可能是等弧. A.①②④ B.①④ C.②④ D.② 解:①不一定,比如半径;③小于半圆的弧叫劣弧;
④直径把圆分成两个半圆,是等弧。 因此只有②正确,故选D. 2.已知:如图,AB是⊙O的直径,CD是弦,AB、CD的延长线交于点E,若AB=2DE,∠E=18°,则∠AOC的度数是( ). A.72° B.60° C.54° D.36° 解:连结OD, ∵AB=2DE, AB=2OD ∴OD=DE ∴∠ODC=2∠E=2×18°=36° ∵OD=OC ∴∠C=∠ODC=36° ∴∠AOC=∠C+∠E=36°+18°=54° 故选C. 3.如图,AB是⊙O的直径,AC是弦,OD∥BC交AC于D,BC=16,则OD的长是( ). A.12 B.10 C.8 D.6 解:∵OD∥BC ∴ ∵AO=OB ∴ ∵BC=16 ∴OD=8 故选C. 4.下列结论中:①长度相等的弧所对的圆心角相等;②相等的圆心角所对的弧相等;③同一个圆中,相等的弦所对的弧相等;④若直径垂直于圆的一条弦,则直径平分弦所对的两条弧.其中正确的个数是( ) A.0个 B.1个 C.2个 D.3个 解:①长度相等的弧不一定是等弧,所对的圆心角不一定相等; ②例如在两同心圆里,相等的圆心角所对的弧显然不相等; ③一条弦对两条弧,一条弦所对的优弧明显不等于另一条弦所对的劣弧; ④由圆的对称性可得。 只有④正确。故选B. 5.如图,⊙O中,∠AOB=2∠COD,则弦AB与2CD的大小关系是( ) A.AB>2CD B.AB=2CD C.AB<2CD D.AB与2CD的大小关系不确定 解:作半径OE平分∠AOB,连结AE、EB ∵∠AOB=2∠COD ∴∠AOE=∠EOB=∠COD ∴AE=EB=CD ∵AB (如图∠AC’B)
故选C. 8.如图,圆中相等的圆周角的对数和相似三角形的对数分别是( ) A.4,2 B.4,6 C.6,6 D.2,2
解:如图,为方便起见,标出∠1—∠8,
利用同弧所对的圆周角相等易得
∠1=∠4,∠2=∠7,∠5=∠8,∠3=∠6;
△ABE∽△DCE,△ADE∽△BCE。
故选A.
9.等腰三角形ABC中,顶角∠BAC=70°,以AB为直径的半圆交BC于点D,则∠BAD的度数为( )
A.55° B.35° C.70° D.90°
解:连结AD
∵AB为直径
∴∠ADB=90°,即AD⊥BC
∵AB=AC,∠BAC=70°
∴∠BAD=70°=35°
故选B.
10.如图,A、B、C三点都在⊙O上,AD⊥BC于D,⊙O的直径AE交BC边于点G,有四个结论:①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
解:①∠BAC不一定是直角,所以AD2=BD·CD不一定成立;
②∵AE为直径,∴∠ABE=90°,只有当AE⊥BC时才有BE2=EG·AE;
③由△ABE∽△ADC可得AE·AD=AB·AC;
④由△AGC∽△BGE可得AG·EG=BG·CG。
故选B.
?
?
圆的认识 圆的基本元素. 圆的对称性. 圆周角. 1.确定一个圆的条件:圆心和半径. 圆心定位置,半径定大小. 以点O为圆心的圆记为“⊙O”,叫作“圆O”. 如图(1):圆心相同,半径不同的圆叫同心圆; 如图(2):半径相同,圆心不同的圆叫等圆. 基本内容讲解 一.圆的基本元素2.弦、直径、半径 (3) 线段AB、AC、BC都是连结圆上两点的线段,这样的线段叫圆的弦;其中弦AB经过圆心,叫圆的直径;而线段OA、OB、OC都是连结圆心和圆上一点的线段,叫圆的半径。 同圆或等圆中,半径都相等; 3.弧、半圆弧(简称半圆)、劣弧、优弧 图中曲线AC、ACB、ABC等都叫做弧,记为 其中弧ACB叫半圆弧,简称半圆; 像弧AC 这样小于半圆的弧叫劣弧; 像弧ABC这样大于半圆的弧叫优弧。 等弧:能够互相重合的弧叫等弧. 4.圆心角 图中,∠AOC、∠BOC都是圆心角。 例1. 下列说法中正确的是( ) ①直径是弦; ②弦是直径; ③半圆是弧,但弧不一定是半圆; ④半径相等的两个半圆是等弧; ⑤长度相等的两条弧是等弧. A.①④ B.①③④ C.①③④⑤ D.①②③④⑤ 解:选B. 例2. 已知:如图,AB是⊙O的直径,CD是任意一条非直径的弦.试说明:AB?CD. 解:连结OC、OD,在△OCD中, ∵OC?OD>CD 又∵AB?OA?OB?OC?OD ∴AB?CD ? 例3. 已知:如图,AB是⊙O的直径,D、E为⊙O上两点,DE的延长线交AB的延长线于点C且CE?OA,若∠AOD?84°,求∠C的度数. 解:连结OE ∵CE?OA,OA?OD?OE ∴∠D?∠OED?2∠C ∵∠AOD?∠D? ∠C ∴∠AOD?3∠C ∵∠AOD?84° ∴∠C?28° 二.圆的对称性 (1)圆是一个旋转对称图形;圆心为其对称中心. 将⊙O中的扇形AOB绕点O逆时针旋转某个角度,画出得到的图形,比较前后两个图形,你发现了什么? 如图,扇形AOB旋转到扇形A ′ OB′的位置,得到 ∠AOB? ∠ A ′ OB′, ,
AB? A ′ B′. ①在一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.
②在一个圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等.
③在一个圆中,如果弦相等,那么它所对的圆心角相等,圆心角所对的弧相等.
上面这三个结论,简称“三量关系”。 例4 如图,在⊙O中, ,∠A?40°, 求∠C的度数. 解:∵ ∴AB?AC ∴∠B?∠C ∵∠A?40° ∴∠C?∠B? 70° ? (2)圆是一个轴对称图形,任意一条直径所在的 直线都是它的对称轴. 如图,在圆形纸片上任意画一条垂直于直径 CD的弦AB,垂足为P,再将纸片沿直径CD 对折,比较AP与BP, 你能发现什么? 得到:AP?BP, ∵AB⊥直径CD于P ∴AP?BP,
这个结论也称“垂径定理”. 例5. 已知:如图,半径为6的⊙O中,弦AB垂直 平分半径OC,求弦AB的长. 解:连结OA,设AB交OC于点E ∵弦AB垂直平分半径OC ∴ , AE?BE ∵⊙O的半径为6 ∴OA?6,OE?3 在Rt△OAE中,
∴AB? ∴弦AB的长为 . 例6.半径为5的⊙O中,弦AB? 6cm,弦CD? 8cm.且AB?? CD,求AB与CD之间的距离. 解:如图(1),连结OA、OC 过O作MN⊥AB于M,交CD于N, ∵AB?? CD ∴MN⊥CD于N ∴AM?MB,CN?ND ∵AB? 6,CD? 8 ∴AM? 3,CN? 4 又∵半径为5 ∴OA?OC? 5 ∴在Rt△AOM及Rt△CON中,
∴MN?OM? ON?4? 3=7 如图(2),同理可得MN?OM?ON?4?3? 1 ∴AB与CD之间的距离是7cm或1cm. (1)(2)(3)(4)(5)三. 圆周角 如图,图(2)所示的角为圆周角. (1)半圆或直径所对的圆周角都相等,都等于90°(直角). (2)90°的圆周角所对的弦是圆的直径(所对的弧是半圆). (3)一条弧所对的圆周角等于该弧所对的圆心角的一半. (4)在同圆或等圆中,同弧或等弧所对的圆周角相等,都 等于该弧所对的圆心角的一半;相等的圆 周角所对的弧相等.例7. 已知:如图,AB是⊙O的直径,AC、AD为 弦,且AD平分∠BAC,若AB?10,AC? 6, 求AD的长. 解:连结BD并延长交AC的延长线于点E,连结BC ∵AB是⊙O的直径 ∴∠ACB?∠ADB?90° ∴BC⊥AE,AD⊥BE 又∵AD平分∠BAC ∴AE?AB,DE?BD ∵AB? 10,AC? 6 ∴CE? AE?AC? 4 , 在Rt△ABC中
在Rt△BCE中,
∴ 在Rt△ABD中,
∴AD? 例8.?? 如图,AB是⊙O的直径,C为⊙O上一点,AD为弦,DE⊥AB于F交AC于E,试问AD2与AE·AC是否相等?为什么? 分析:解:AD2与AE·AC相等。 延长DE交⊙O于H ∵DE⊥AB ,AB是⊙O的直径 ∴ ∴∠ADH? ∠C 又∵∠DAE? ∠CAD ∴△ADE∽△ACD ∴ ∴AD2? AE·AC
另解:连结BD ∵AB是⊙O的直径 ∴∠ADB? 90°
又∵DE⊥AB ∴∠ADE? ∠B ∵∠C? ∠B ∴∠ADE? ∠C 又∵∠DAE? ∠CAD ∴△ADE∽△ACD ∴ ∴AD2? AE·AC 例9.?? 如图,AB为半圆O的直径,弦AD、BC交于点P,CD? 4,AB? 5,求cos∠BPD的值. 分析:解:连结BD ∵AB为半圆O的直径 ∴∠ADB? 90° 在△BPD中,cos∠BPD? ∵∠C? ∠A,∠CDP? ∠PBA ∴△CDP∽△ABP ∴ ∴cos∠BPD? ∵CD? 4,AB? 5 cos∠BPD? ? 小结 1. 与圆有关的概念:确定一个圆的条件是 圆心 和半径. 了解圆中的基本概念:弦、直径、半径、弧、半圆弧(简称半圆)、劣弧、优弧、等弧。注意只有能够互相重合的弧叫等弧. 2.由圆的旋转对称性得到圆心角、弧、弦
“三量关系” ①在一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等. ②在一个圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等. ③在一个圆中,如果弦相等,那么它所对的圆心角相等,圆心角所对的弧相等. 由圆的轴对称性得到“垂径定理”。也就是说,由直径垂直于弦可以得到三个平分,由直径CD垂直于弦AB于点P,可以得到AP? BP, ? 3.圆心角及圆周角的有关结论: (1)半圆或直径所对的圆周角都相等,都等于90°(直角). (2)90°的圆周角所对的弦是圆的直径(所对的弧是半圆). (3)一条弧所对的圆周角等于该弧所对的圆心角的一半. (4)在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等. 课后练习 1.下列说法中正确的是( ) ①??? 过圆心的线段是直径; ②直径相等的两个圆是等圆; ③小于半圆的弧是优弧; ④一条弦把圆分成两条弧,这两条弧不可能是等弧. A.①②④ B.①④ C.②④ D.②2.已知:如图,AB是⊙O的直径,CD是弦,AB、CD的延长线交于点E,若AB=2DE,∠E=18°,则∠AOC的度数是( ). A.72° B.60° C.54° D.36° 3.如图,AB是⊙O的直径,AC是弦,OD∥BC交AC于D,BC=16,则OD的长是( ). A.12 B.10 C.8 D.6 4.下列结论中:①长度相等的弧所对的圆心角相等;②相等的圆心角所对的弧相等;③同一个圆中,相等的弦所对的弧相等;④若直径垂直于圆的一条弦,则直径平分弦所对的两条弧.其中正确的个数是( ) A.0个 B.1个 C.2个 D.3个 5.如图,⊙O中,∠AOB=2∠COD,则弦AB与2CD的大小关系是( ) A.AB>2CD B.AB=2CD C.AB<2CD D.AB与2CD的大小关系不确定? 6.⊙O中弦AB与直径CD相交成30°,交点为P,且分CD为2和10两段,则弦AB的长度为( ) A.2 B.4 C. D. 7.⊙O中弦AB把圆分成1:3两部分,则圆周角∠ACB的度数为( ) A.45° B.135° C.45°或135° D.以上答案都不对 ? ? ? 8.如图,圆中相等的圆周角的对数和相似三角形的对数分别是( ) A.4,2 B.4,6 C.6,6 D.2,2 9.等腰三角形ABC中,顶角∠BAC=70°,以AB为直径的半圆交BC于点D,则∠BAD的度数为( ) A.55° B.35° C.70° D.90° ? ? ? 10.如图,A、B、C三点都在⊙O上,AD⊥BC于D,⊙O的直径AE交BC边于点G,有四个结论:①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AG;④AG·EG=BG·CG.其中正确的个数是( ) A.1个 B.2个 C.3个 D.4个 练习解答 1.下列说法中正确的是( ) ①过圆心的线段是直径; ②直径相等的两个圆是等圆; ③小于半圆的弧是优弧; ④一条弦把圆分成两条弧,这两条弧不可能是等弧. A.①②④ B.①④ C.②④ D.② 解:①不一定,比如半径;③小于半圆的弧叫劣弧;
④直径把圆分成两个半圆,是等弧。 因此只有②正确,故选D. 2.已知:如图,AB是⊙O的直径,CD是弦,AB、CD的延长线交于点E,若AB=2DE,∠E=18°,则∠AOC的度数是( ). A.72° B.60° C.54° D.36° 解:连结OD, ∵AB=2DE, AB=2OD ∴OD=DE ∴∠ODC=2∠E=2×18°=36° ∵OD=OC ∴∠C=∠ODC=36° ∴∠AOC=∠C+∠E=36°+18°=54° 故选C. 3.如图,AB是⊙O的直径,AC是弦,OD∥BC交AC于D,BC=16,则OD的长是( ). A.12 B.10 C.8 D.6 解:∵OD∥BC ∴ ∵AO=OB ∴ ∵BC=16 ∴OD=8 故选C. 4.下列结论中:①长度相等的弧所对的圆心角相等;②相等的圆心角所对的弧相等;③同一个圆中,相等的弦所对的弧相等;④若直径垂直于圆的一条弦,则直径平分弦所对的两条弧.其中正确的个数是( ) A.0个 B.1个 C.2个 D.3个 解:①长度相等的弧不一定是等弧,所对的圆心角不一定相等; ②例如在两同心圆里,相等的圆心角所对的弧显然不相等; ③一条弦对两条弧,一条弦所对的优弧明显不等于另一条弦所对的劣弧; ④由圆的对称性可得。 只有④正确。故选B. 5.如图,⊙O中,∠AOB=2∠COD,则弦AB与2CD的大小关系是( ) A.AB>2CD B.AB=2CD C.AB<2CD D.AB与2CD的大小关系不确定 解:作半径OE平分∠AOB,连结AE、EB ∵∠AOB=2∠COD ∴∠AOE=∠EOB=∠COD ∴AE=EB=CD ∵AB
同课章节目录
