７.５一次函数的简单应用（２）

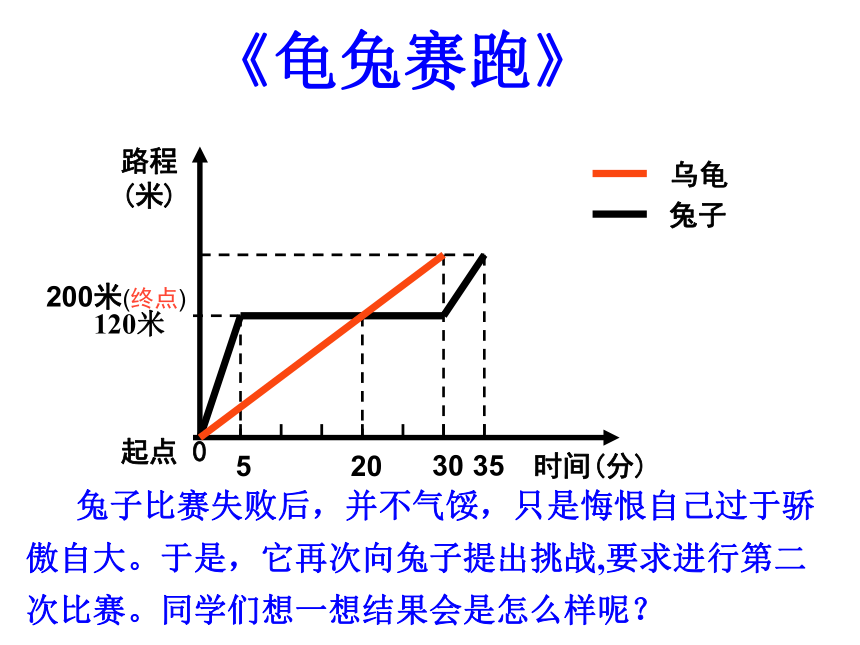
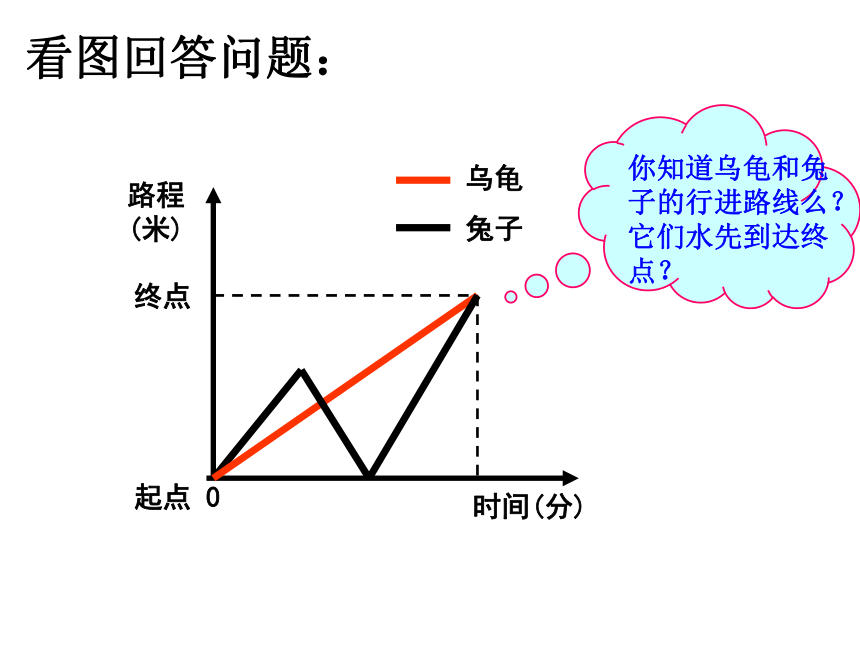
课件26张PPT。7.5 一次函数的简单应用(2)复习 回顾： 在运用一次函数解决实际问题时，首先判断问题中的两个变量之间是不是一次函数关系？当确定是一次函数关系时，可求出函数解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果。乌龟兔子时间(分)3520305起点 0200米(终点)路程(米)120米 兔子比赛失败后，并不气馁，只是悔恨自己过于骄傲自大。于是，它再次向兔子提出挑战,要求进行第二次比赛。同学们想一想结果会是怎么样呢？《龟兔赛跑》乌龟兔子时间(分)起点 0终点路程(米) 这一次,兔子让乌龟先跑若干分钟,然后它开始追赶,结果它们同时到达终点.你也能用函数图象表示吗?试试看.
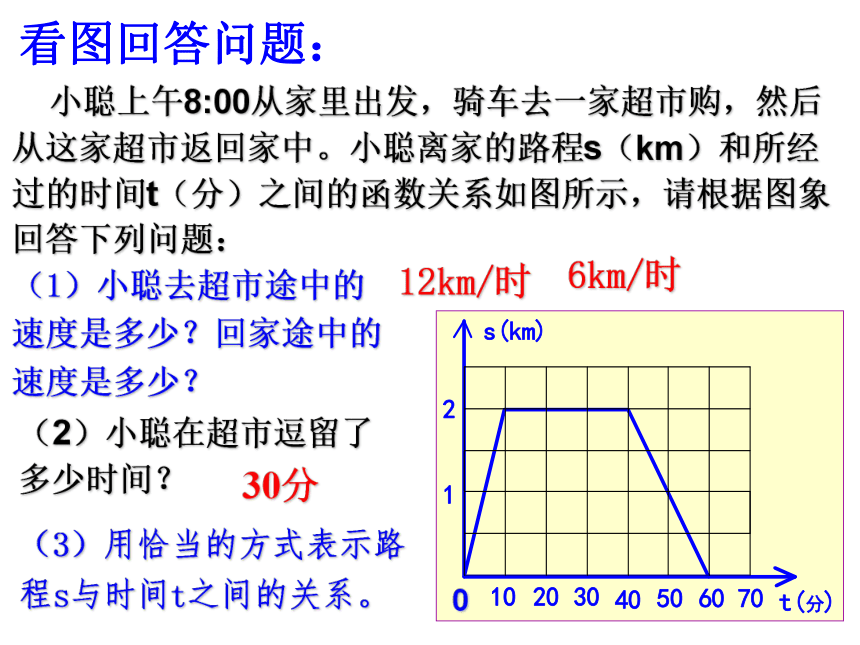
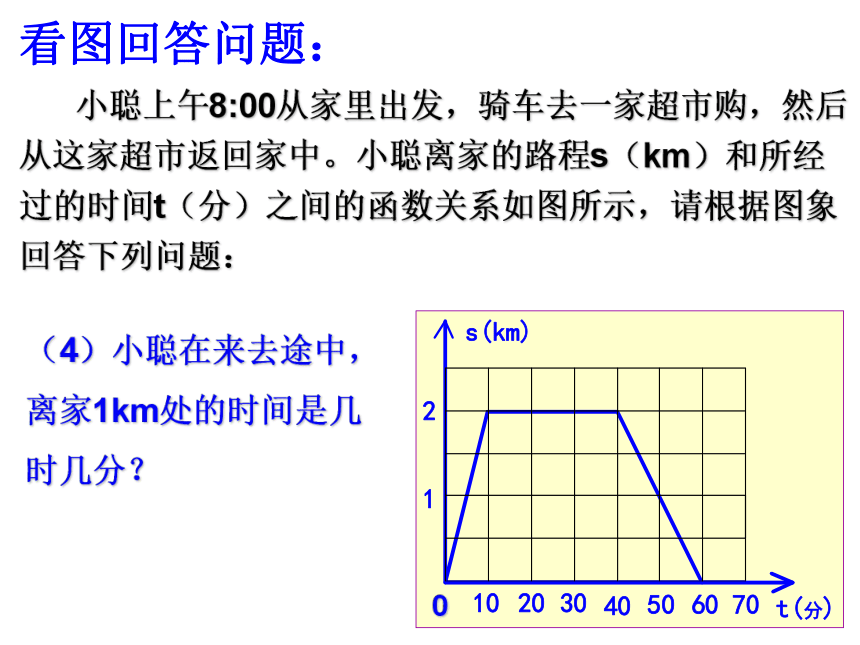
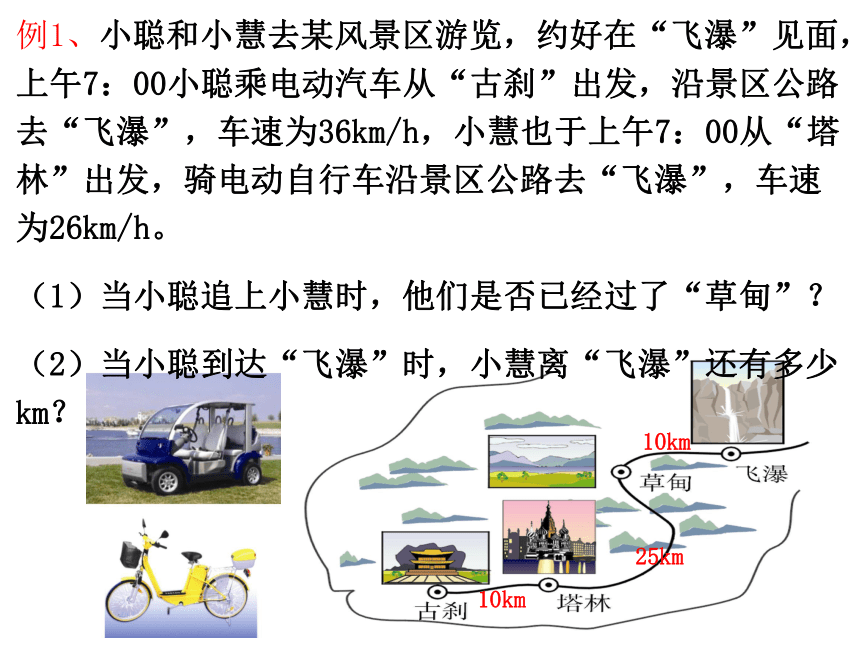
乌龟兔子时间(分)起点 0终点路程(米)看图回答问题： 小聪上午8:00从家里出发，骑车去一家超市购，然后从这家超市返回家中。小聪离家的路程s（km）和所经过的时间t（分）之间的函数关系如图所示，请根据图象回答下列问题：（1）小聪去超市途中的速度是多少？回家途中的速度是多少？12km/时6km/时看图回答问题：（2）小聪在超市逗留了多少时间？30分（3）用恰当的方式表示路程s与时间t之间的关系。（4）小聪在来去途中，离家1km处的时间是几时几分？ 小聪上午8:00从家里出发，骑车去一家超市购，然后从这家超市返回家中。小聪离家的路程s（km）和所经过的时间t（分）之间的函数关系如图所示，请根据图象回答下列问题：看图回答问题：例1、小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？10km10km25km例1、小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？分析：⑴两个人是否同时起步？
⑵在两个人到达之前所用时间是否相同？所行驶的路
程是否相同？出发地点是否相同？两个人的速度各是多少？
⑶这个问题中的两个变量是什么？它们涉及的是什么函数关系？⑷如果用S表示路程，t表示时间，那么他们的函数解析式是一样的吗？他们各自的解析式分别是什么？小聪的解析式为 ；小慧的解析式为 ；S1=36tS2=26t+10例1、小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？解：设经过t时，小聪与小慧离“古刹”的路程分别为S1、S2，
由题意得：S1=36t， S2=26t+10将这两个函数解析式画在同一个直角坐标系上，观察图象，得36S1=36tS2=26t+10⑴两条直线S1=36t， S2=26t+10的交点坐标为 ；（1，36）这说明当小聪追上小慧时，S1=S2=36 km，即离“古刹”36km，已超过35km，也就是说，他们已经过了“草甸”S1=36tS2=26t+1042.5⑵当小聪到达“飞瀑”时，即S1=45km，此时S2=42.5km。
所以小慧离“飞瀑”还有45－42.5=2.5（km）思考：用解析法如何求得这两个问题的结果？例1、小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为36km/h，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km/h。
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？只要把两条解析式联列成方程组，求出方程组的解，即为两条直线交点坐标。 你能从图象中直接获取哪些信息呢?与周围同学交流一下吧!并展示你的成果.t(分)3000S (米)李某家023151、李某同学每天早上都与爸爸一起参加长跑训练，他们沿相同的路线从家里跑到学校，两人所跑的路程s与时间t之间的函数关系如图所示，(假设两人均为匀速运动)请思考:
1）爸爸追上李某需要几分钟？
2）李某家到学校的距离为多少米？
3）李某跑到学校需要几分钟？ 5学校2010试一试答: 爸爸追上李某花了10分钟;
因为爸爸的速度为300米／分钟,他花了18分钟跑到学校,所以李某家到学校的距离为5400米;
而李某的速度为200米／分钟,所以李某跑到学校需要27分钟. t(分)3000S (米)李某家023155学校2010解:由图象信息可得:
S李＝200t(t≥0)
S爸＝300t－1500(t≥5)
所以当t＝23时，
S爸＝5400 .
即:李某家到学校的距离为5400米.
当S李＝5400时,
t＝27 .
即:李某跑到学校需要27分钟.?（1）说出甲、乙两物体的初始位置，并说明开始时谁前谁后？2、已知甲、乙两物体沿同一条直线同时、同向匀速运动，它们所经过的路程s与所需时间t之间的关系如图所示.甲物体在离起点2米处，乙物体在起点。甲在前乙在后.试一试（3）求出两直线的交点坐标，并说明实际意义.2秒时乙物体追上甲物体。2秒前甲先乙后
2秒后乙先甲后。（2）分别求出甲、乙的路程s关于时间t的函数解析式.(2,3)例2、清华大学登山队某队员在攀登念青唐古拉中央峰时，其距离地面的海拔高度s（米）与时间t（小时）之间的函数关系如图所示。(假设往返均为匀速运动)
（1）你能分别求出0≤t≤12和t＞12时s与t的函数关系式吗?
（2）一般情况下，人到达海拔3000米左右地区时,就开始出现呼吸频率和心率加快、疲乏、头痛等不良症状，那么运动员在这次登山运动中出现这种症状大约会持续多久?S (米)t (小时)0121648002400BA84 S1＝400t（ 0≤ t≤12）
S2＝－600t+12000（t＞12） OA所在的直线是什么函数? AB呢?请解答!CS (米)t (小时)0121648002400解:由图象信息可得:

当S1＝3000时,t＝7.5
当S2＝3000时,t＝15
所以运动员出现这种症状大约会持续15-7.5＝7.5个小时。BA843000S1＝400t（ 0≤ t≤12）
S2＝－600t+12000（t＞12）C练一练： 2、去年暑假时，学校组织部分师生去云南旅游。在当地一个著名景点玉龙雪峰，早上九点时大家先从海拔2400米的候车厅乘坐旅游公司的大巴到达海拔4000米的玉龙大索道的出发站，然后乘坐缆车上到海拔4500米处，最后步行到的峰顶，那么你能否选出能正确反映老师这次旅行过程的一副图吗？并请你详细为大家介绍一下老师此次爬山的行程（说出时间、地点、速度）？ 练一练：例3、北京某厂和上海某厂同时制成电子计算机若干台，北京厂可支援外地10台，上海厂可支援外地4台，现在决定给重庆8台，汉口6台。假定每台计算机的运费如下表：（1）若总运费为8400元，上海运往汉口应是多少台？（2）若要求总运费不超过8200元，共有几种调运方案？（3）求出总运费最低的调运方案，最低总运费是多少元？ 某家电信公司提供两种方案的移动通讯服务的收费标准如下表：如果请你选择其中一种方案，应如何选择？做一做本节课你学到了什么?提高拓展