一次函数的复习(浙江省衢州市开化县)

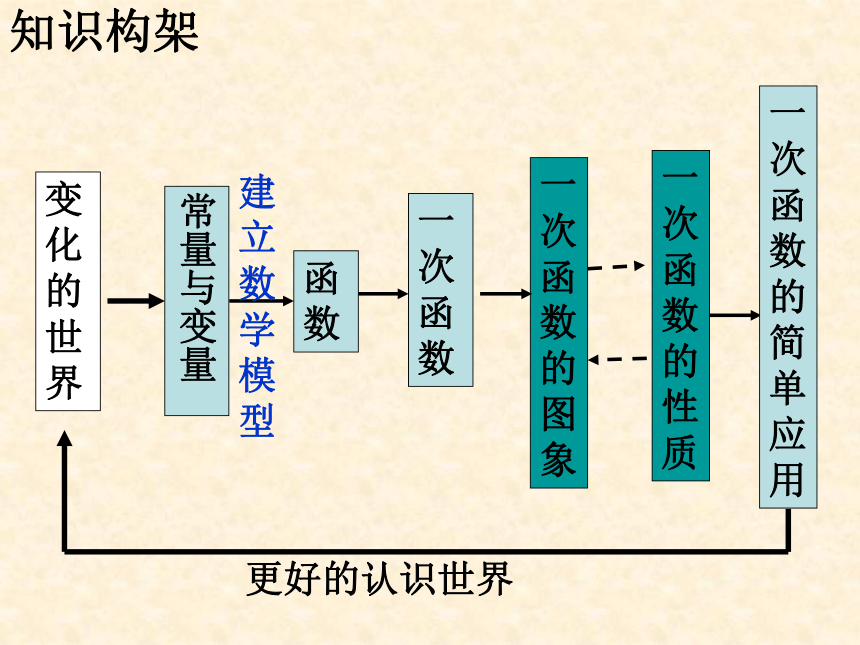
课件30张PPT。第七章 一次函数7.1，常量和变量7.2，认识函数7.4，一次函数的图象7.3，一次函数7.5，一次函数的简单应用知识构架变化的世界函数一次函数一次函数的图象一次函数的性质建立
数学模型常量与变量一次函数的简单应用更好的认识世界技能要求1.C=2πr有几个量？常量有_____变量有_____2,πC,r2.百米赛跑中,常量有_____,变量有_______10秒内比谁跑得快,常量有_____,变量有_______就算在同一种变化过程中,常量和变量也不是绝对不变的,所以常量和变量是相对的不是绝对的时间时间.速度路程路程.速度3.某地区从95年底开始,沙漠面积每年几乎以相同的速度增长,据有关报道,到2001年底,该地区沙漠化面积已从98年底的100.6万公顷扩展到101.2万公顷,其中常量有__________________
变量有_________________每年沙漠面积化速度时间沙漠化总面积请观察加油机为汽车加油过程中，
哪些量在改变，哪些量不变？在一个过程中,固定不变的量称为常量
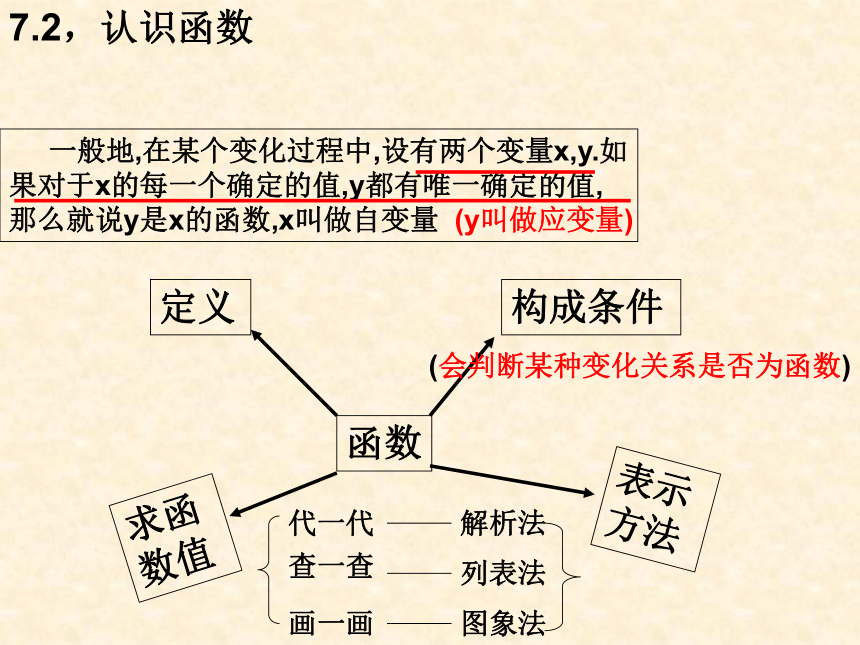
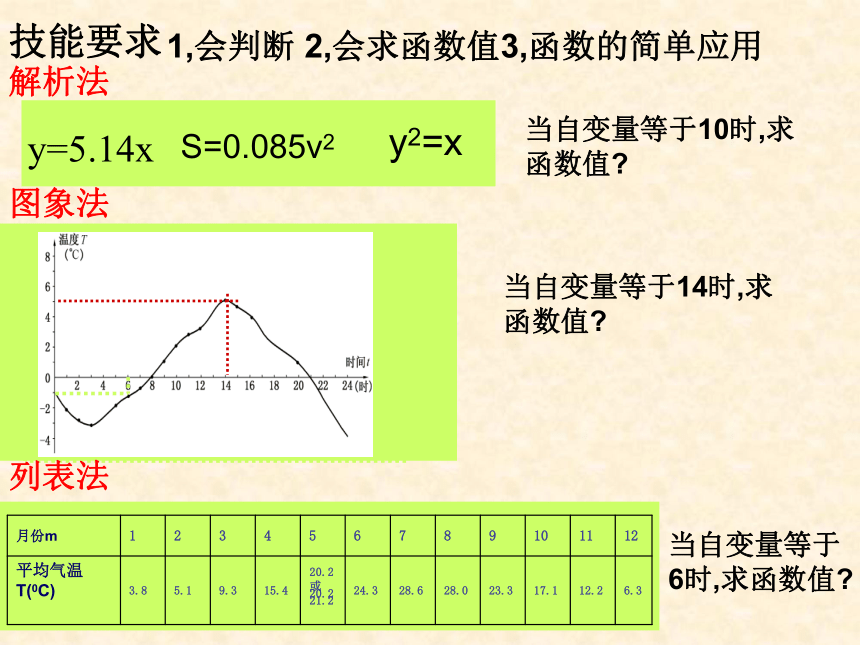
在一个过程中,可以取不同数值的量称为变量7.1常量与变量7.2，认识函数函数定义表示方法构成条件求函数值 一般地,在某个变化过程中,设有两个变量x,y.如果对于x的每一个确定的值,y都有唯一确定的值,那么就说y是x的函数,x叫做自变量 (y叫做应变量)(会判断某种变化关系是否为函数)解析法列表法图象法查一查代一代画一画解析法y=5.14x图象法列表法技能要求y2=x1,会判断 2,会求函数值3,函数的简单应用S=0.085v220.220.2或21.2当自变量等于10时,求函数值?当自变量等于14时,求函数值?当自变量等于6时,求函数值?3,函数的简单应用①会列简单实际问题中的函数解析式②已知自变量的值,求相应的函数值③已知函数值,求相应自变量的值④求函数自变量的取值范围与列方程的过程相似(列出等量关系)代入求值代如求值边长＞0时间,路程,速度,费用≥0X取全体实数分母不能为零根号内≥0…….例: 游泳池应定期换水,某泳池在一次换水前存水936立方米,换水时打开排水孔,以每小时312立方米的速度将水排出,设放水的时间为t,泳池内的存水量为Q立方米1,求Q关于t的函数解析式和自变量t的取值范围?解: Q关于t的函数解析式是Q=936-312t∵ t ≥ 0 , 936≥ Q ≥ 0∴解得0≤t ≤3,即自变量t的取值范围是0≤t ≤3练习:等腰三角形的周长为10,若底边长为x,腰长为y,则y与x的函数关系式是_______________,自变量x的取值范围是___________ 当x=4时,y=____,当y =4时,x=_____23y=- x/2 +50≤x≤57.3，一次函数 一次函数
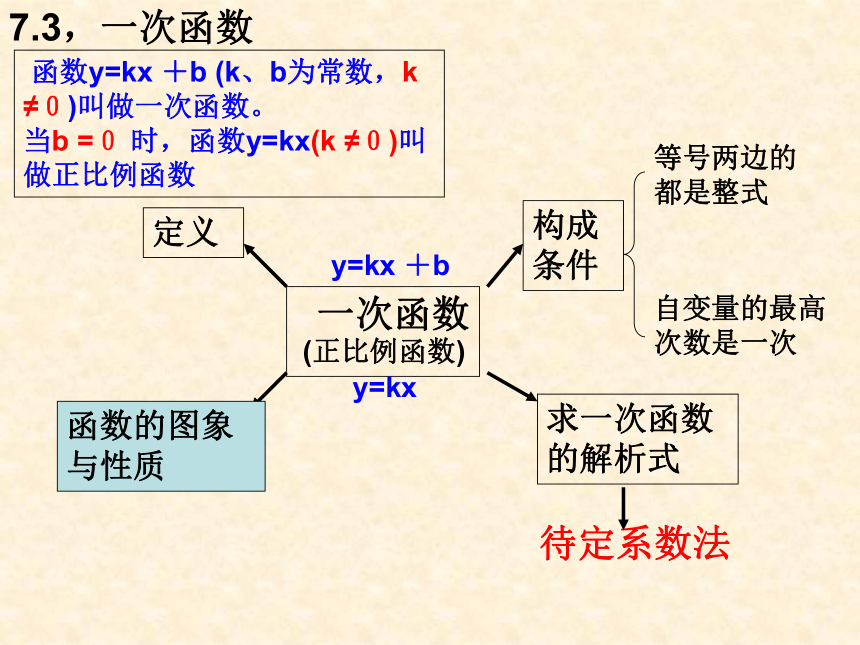
定义求一次函数的解析式构成条件函数的图象与性质 函数y=kx ＋b (k、b为常数，k ≠０)叫做一次函数。
当b =０ 时，函数y=kx(k ≠０)叫做正比例函数(正比例函数)y=kx ＋by=kx等号两边的都是整式自变量的最高次数是一次待定系数法1,下列函数中，哪些是一次函数？哪些是正比例函数？是一次函数
不是正比例函数不是一次函数,不是正比例函数是一次函数
不是正比例函数是一次函数
是正比例函数不是一次函数
不是正比例函数（1）等号两边的代数式都是整式；
（2）自变量的次数是一次；技能要求:1,会判断2,用待定系数法确定一次函数关系式2,判断下列变量之间的关系是否为一次函数(利息与税收) 某种储蓄的月利率是0.16%,存入1000元本金后,
(1)利息y1与所存月数x之间的关系
(2)本息和y2与所存月数x之间的关系y1 =1.6xy1 =1.6x+10002,用待定系数法确定一次函数关系式(即确定K或b的值)待定系数法1,设所求的一次函数解析式为y=kx ＋b,其中K,b是待定的常数2,把两对已知的自变量与函数的对应值分别代入y=kx ＋b,得到关于k,b的二元一次方程组3,解出这个关于K,b二元一次方 程组,求出K,b的值4,把求得的K,b的值代入y=kx ＋b,就得到所求的一次函数关系式了已知y是x的一次函数,且当X=-3时,Y=7,当X=3时,Y=-5,求这个一次函数的解析式.解:设y=kx+b将x=-3,y=7
x=3,y=-5代入得-3k+b=73k+b=-5k=-2b=1解得∴这个一次函数解析式为y=-2x+1练习3、函数 是正比例函数，则m=_______ n=________)5()5(4+--=-nxmym1,已知y是x的正比例函数,且当X=-2时,Y=8, 则这个正比例函数的解析式是___________.2,已知y是x的一次函数,且当X=-3时,Y=10,当X=6时,Y=-5,则这个一次函数的解析式是____________.y=-4xy=-3/5x+5-5-57.4，一次函数的图象在平面直角坐标系中,画出下列函数的图象(两点法)解析:当x=0时,y=0 当x=2时,y=1所以图象一定过(0,0)和(2,1)解析:当x=0时,y=2 当x=2时y=3所以图象一定过(0,2)和(2,3)与坐标轴的交点是_____?围成的面积为______y=kx(k为常数,且k≠0)
它的图象是一条经过_________的直线
(过原点的直线一定是y=kx形式),
且与坐标轴的交点为__________
y=kx+b(k,b为常数,且k≠0)
它的图象是一条不经过原点的直线
(不经过原点的直线是y=kx+b形式)
且与y轴的交点为(0,___)
与x轴的交点为(___,0)原点(0,0)原点(0,0)b-b/ky=kxy=kx+b正比例函数y=kx（k≠0)的性质：
　　⑴当k>0时，图象过______象限；y随x的增大而______
　　⑵当k<0时，图象过______象限；y随x的增大而____。一、三增大二、四减小正比例函数y=kx(k≠0)的图象是过点（____）的_________。
0，0 一条直线一次函数的图象的性质 k < 0一、二、三一、三、四一、二、四二、三、四 k > 0 k < 0 b < 0 b < 0 b > 0 b > 0 k > 0 k > 0 k < 0 k < 0 b < 0 b < 0 b > 0 b > 0 k > 0补充： K相等<=>平行1、已知函数y=kx+b与函数y=2x+3平行，则k=_____22、y=-x+1是由函数y=-x经过_______________得到的 y=-x-5是由函数y=-x经过_______________得到的 向上平移一个单位向下平移五个单位3、若一次函数y=kx+b 与y=-3x+2平行,则当x2 ＞x1
则y2_____ y1　＜4、两直线 和
在同一平面直角坐标系内的图象可能
是 ( )假设找矛盾排除A7.5，一次函数的简单应用1,确定两个变量是否构成了一次函数关系(判断依据:一次函数的图象是一条直线)2,运用一次函数图象解决简单的问题ts3,利用一次函数的图象，求二元一次方程组的解（或近似解）(龟兔赛跑)ts(你能编一个故事吗)3,利用一次函数的图象，求下列二元一次方程组的解（或近似解）x+y=2
y= 2 x-1??y=-x+2??y= 2x-1解:整理得得它们图象的交点为(1,1)所以该二元一次方程组的解是第七章 一次函数7.1，常量和变量7.2，认识函数7.4，一次函数的图象7.3，一次函数7.5，一次函数的简单应用1,确定一次函数的函数解析式例1(原型题)已知y是x的一次函数,且当X=-3时,Y=7,当X=3时,Y=-5,求这个一次函数的解析式.解:设y=kx+b将x=-3,y=7
x=3,y=-5代入得-3k+b=73k+b=-5k=-2b=1解得∴这个一次函数解析式为y=-2x+1两对x与y的对应值待定系数法这种解题的方法我们叫做___________确定一次函数的函数解析式例2(变形1)已知y是x的一次函数, 且它的图象过A(-3,7)和B(3,-5),求这个一次函数的解析式.解:设y=kx+b将x=-3,y=7
x=3,y=-5代入得-3k+b=73k+b=-5k=-2b=1解得∴这个一次函数解析式为y=-2x+1两个点的坐标两对x与y的对应值确定一次函数的函数解析式解:设y=kx+b将x=0,y=-3
x=-6,y=0代入得b=-3-6k+b=0k=-1/2b=-3解得∴这个一次函数解析式为y=-1/2x - 3-3-6例3(变形2)已知y是x的一次函数, 它的图象如下图
所示,则这个一次函数的解析式为____________y=-1/2x - 3两个点的坐标两对x与y的对应值与坐标轴的两个交点坐标确定一次函数的函数解析式例4(变形4) 已知一次函数的图象经过点A(-3,7)且与y=-2x+5平行;解:设y=kx+b将x=-3,y=7代入得y=-2x+bb=1解得∴这个一次函数解析式为y=-2x+1∵与y=-2x+5 平行∴k=-2 ∴ y=-2x+b确定一次函数的函数解析式例5(整体思维)已知y-1与x+2成正比例函数关系,且当x=1,y=7求y关于x的函数解析式解:设y-1=k(x+2)将x=1,y=7代入得k=2解得∴y关于x的解析式是y=2x+57-1=k(1+2)∴ y-1关于x+2的解析式是y-1=2(x+2)整体思维中括号很重要（0≤x ≤500）（500＜x ≤2000）y=5%xy=500x5%+ (x-500)x10%例：按国家有关规定，全月应纳税所得额不超过500元的税率为5%，超过500至2000元部分的税率为10%，设全月应纳所得税为y,求y关于x的函数解析式和自变量的取值范围。需要分类讨论的函数关系解：即y=0.1x-251，小李的月薪为2400元，则月纳税所得额为________,应缴个人所得税为_____________2，老李的月薪为3400元，则月纳税所得额为________,应缴个人所得税为________400y=5%x400=201400y=0.1x1400-25
=115500100015002000每月应纳个人所得税 (y)050100150200每月应纳税所得额(x)（0≤x ≤500）（500＜x ≤2000）y=5%xy=0.1x-25画出属于它的函数图象下列函数关系哪些需要分类讨论?221214523t(小时)S(千米)分类讨论0≤t ≤1S=2t1≤t ≤4S=24≤t ≤5S=t-2xxyy设y=kx代入得k=1所以y=x1设y=kx+b代入,解得k=1,b=1 所以y=x+1当小兔子跑了 4.25小时时,他经历的路程s=______2.25千米出租车电话费(月租)电费…水费 个人所得税…房租(月租+水电费)你能想出生活中的其他例子,也是属于这样的函数图象吗?你能求出蓝色的两条线段所代表的函数解析式吗?