7.6余角和补角

课件20张PPT。 复习如图:∠ABC=70°,BD平分∠ABC.
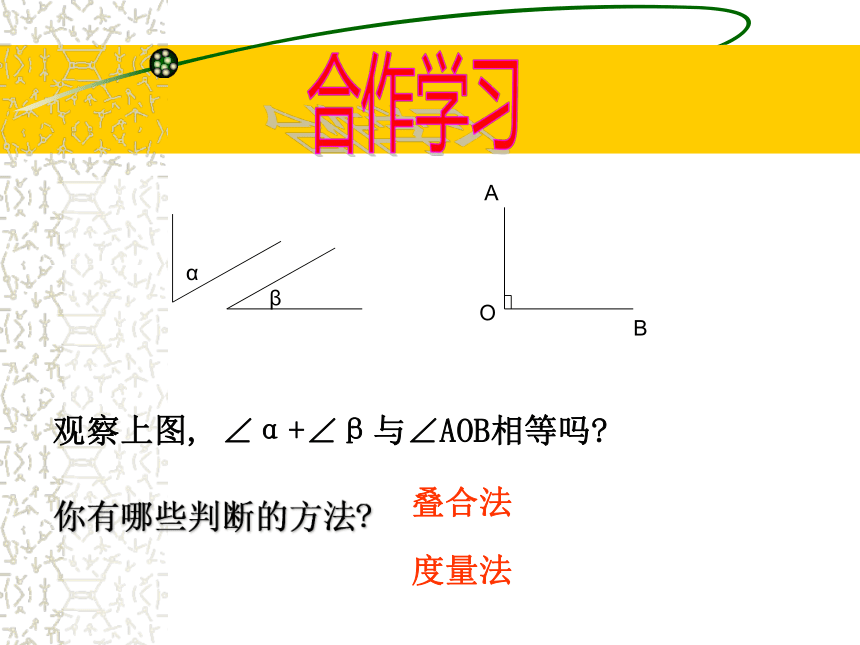
则∠DBA=______°.BDAC357.6余角和补角合作学习AOB观察上图, ∠α+∠β与∠AOB相等吗?你有哪些判断的方法?叠合法度量法互为余角的概念如果两个锐角的和是一个直角,就称这两个角互为余角,简称互余.也可以说其中一个角是另一个角的余角.
余数学表达式:∠α是∠β的余角
∠β是∠α的余角合作学习AOB观察上图, ∠ +∠ 与∠AOB相等吗?你是怎样判断的?叠合法度量法互为补角的概念如果两个角的和是一个平角,就称这两个角互为补角,简称互补.也可以说其中一个角是另一个角的补角.

数学表达式:
补∠α是∠β的补角
∠β是∠α的补角例: 已知∠α=27°,求∠α的余角和补角的度数. 解:∠α的余角=90°－ ∠α=90°－27°=63°
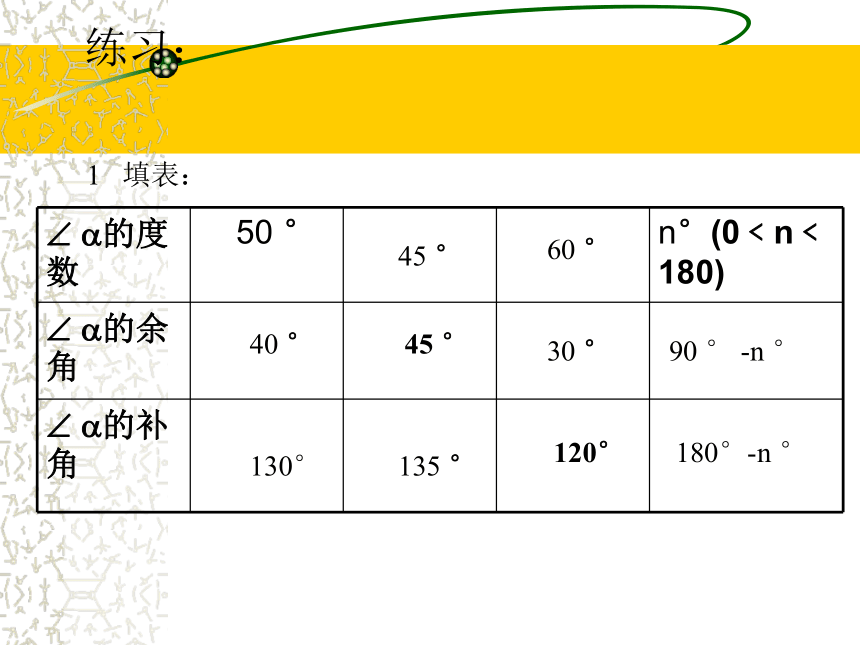
∠α的补角=180°－ ∠α=180°－27°=153°公式:∠α的余角=90°－ ∠α∠α的补角=180°－ ∠α=90°∠α的补角－ ∠α的余角余补练习：1 填表： 40 ° 130°45 °135 °60 °30 °90 ° -n °180°-n °45 °120°判断：
①一个角的余角一定是锐角.（ ）
②一个角的补角一定是钝角.（ ）
③若∠1+∠2+∠3=90°，那么∠1、∠2、∠3互为余角.（ ）
④两个角互补，那么这两个角中，必定一个是锐角，另一个是钝角. ( )
练一练
????比一比，谁完成的最好1、若∠1与∠2互余， ∠1+∠2= °，若∠1与∠2互补，则∠1+∠2=　　 ° 2、30°角的余角为 　 °，补角为　 °， 75°30′的余角为 ，补角为 。 n°(0 ＜ n＜90)的余角为 ，补角为 。901806015014°30′104°30′(90°-n°)(180°-n°)∠COD∠BOD∠AOD做一做∵ ∠ １＋ ∠ ３＝ ４２°＋ ４８°＝９０ °，
∴ ∠ １与 ∠ ３互余.
∵ ∠ １＋ ∠ ２＝ ４２°＋ １３８°＝１８０ °，
∴ ∠ １与 ∠ ２互补.∵ ∠ＢＯＤ＋ ∠ＤＯＣ＝ ∠ＢＯＣ＝ ∠ＡＯＣ＝Ｒt ∠
∴ ∠ＢＯＤ与 ∠ＤＯＣ互余．
∵ ∠ＡＯＣ＋∠ＢＯＣ＝１８０　∠ＡＯＤ＋∠ＢＯＤ＝１８０ °，
∴ ∠ＡＯＣ与∠ＢＯＣ互补， ∠ＡＯＤ＋∠ＢＯＤ互补．余角的性质 同角或等角的余角相等(1)已知∠1与∠2互为余角,
∠1与∠3互为余角,
则∠2与∠3是什么关系?数学表达式:∵∠1+∠2=90°
∠1+∠3=90°∴∠2=∠3同角的余角相等(2)已知∠1与∠2互为余角,
∠3与∠4互为余角,若∠1=∠3
则∠2与∠4是什么关系?数学表达式:∵∠1+∠2=90°
∠3+∠4=90°
∠1=∠3∴∠2=∠4等角的余角相等23利用三角尺画出∠1的余角补角的性质 同角或等角的补角相等
同角情况:
∵∠1+∠2=180°
∠1+∠3=180°
∴∠2=∠3
(同角的补角相等) 等角情况:
∵∠1+∠2=180°
∠3+∠4=180°
∠1=∠3
∴∠2=∠4
(等角的补角相等)例１　　如右图，已知∠ ＡＯＣ＝ ∠ＢＯＤ＝Ｒt ∠．指出图中还有哪些角相等，并说明理由． 解：∠ ＡＯＢ＝ ∠ＣＯＤ理由：　　∵ ∠ ＡＯＣ＝ ∠ＢＯＤ＝Ｒt ∠，
　同角的余角相等　∴ ∠ ＡＯＢ＋ ∠ ＢＯＣ＝Ｒt ∠，
　　∠ ＣＯＤ＋ ∠ ＢＯＣ＝Ｒt ∠，即　　∠ ＡＯＢ与∠ ＣＯＤ都是∠ ＢＯＣ的余角，　∴ ∠ ＡＯＢ＝ ∠ＣＯＤ　（　　　　　　　　）如图 ,请问∠1与∠3相等吗？并说明理由. AOEBCD做一做1234例2 、已知一个角的补角是这个角的余
角的4倍，求这个角的度数． 解：设这个角为x度,根据题意,得
180— x = 4（90—x）
解得 x=60（度）答：这个角为60°小结?1＋ ?2＝90°?1＋ ?2＝180°同角(等角)的余角相等同角(等角)的补角相等如果两个锐角的和是一个直角，我们就说这两个角互为余角，简称互余如果两个角的和是一个平角，我们就说这两个角互为补角，简称互补①互余、互补都是指两个角；
②互余、互补只与角度大小有关，与位置无关。下图中，OA是表示南偏西30o方向上的一条射线，仿照这条射线，画出表示下列方向的射线：（1）北偏西20o；（2）南偏东60o； （3）西南方向（即南偏西45o）。30o20o60o45o表示（1）、（2）方向的两条射线所成的角是多少度？表示（2）、（3）方向的两条射线所成的角呢？140o105o练一练如图，直线CD经过点O，且OC平分∠AOB。试判断∠AOD与∠BOD的大小关系，并说明理由。ODABC答：∠AOD=∠BOD∵∠AOD与∠AOC互补， ∠BOD与∠BOC互补∴∠AOD=180°- ∠AOC
∠BOD=180°-∠BOC又∵OC平分∠AOB
∴∠AOD=∠BOD（等角的补角相等）∴∠AOC=∠BOC如图:三角形ABC中,∠ACB=Rt∠, CD是AB边上的高线.
指出图中互余的角和相等的角.并说明理由.练一练