【新课堂】华师版数学九年级下册 26.2.2 二次函数y=ax2+bx+c的图象和性质 教案
文档属性
| 名称 | 【新课堂】华师版数学九年级下册 26.2.2 二次函数y=ax2+bx+c的图象和性质 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 495.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 15:05:53 | ||
图片预览

文档简介
26.2.2 二次函数y=ax2+bx+c的图象和性质
课题 26.2.2 二次函数y=ax2+bx+c的图象和性质 单元 第26章 学科 数学 年级 九年级
学习 目标 1.熟练画出二次函数y=ax2+c 的函数图象. 2.掌握并能够正确运用二次函数y=ax2+c 的特点与性质.
重点 运用二次函数y=ax2+c 的特点与性质.
难点 掌握并能够正确运用二次函数y=ax2+c 的特点与性质.
教学过程
教学环节 教师活动 学生活动 设计意图
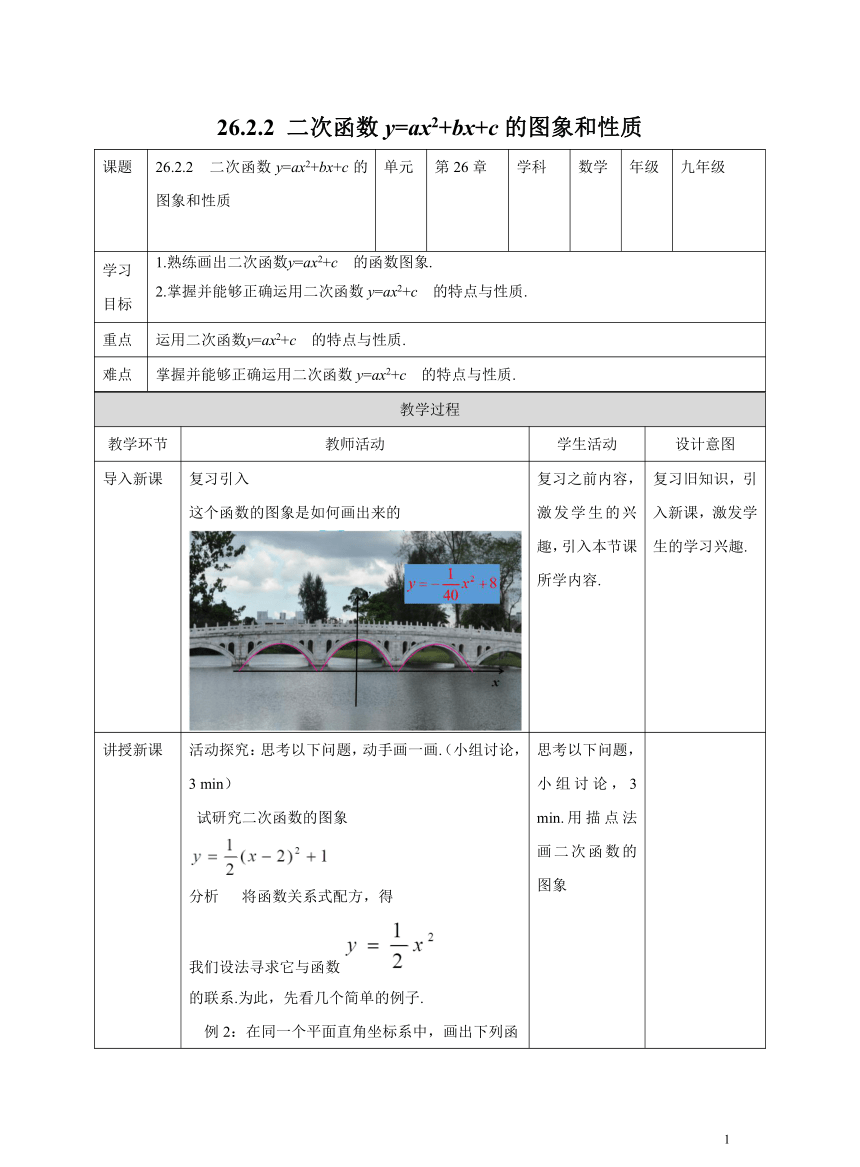
导入新课 复习引入 这个函数的图象是如何画出来的 复习之前内容,激发学生的兴趣,引入本节课所学内容. 复习旧知识,引入新课,激发学生的学习兴趣.
讲授新课 活动探究:思考以下问题,动手画一画.(小组讨论,3 min) 试研究二次函数的图象 分析 将函数关系式配方,得 我们设法寻求它与函数 的联系.为此,先看几个简单的例子. 例2:在同一个平面直角坐标系中,画出下列函数与的图象. 解:列表 在平面直角坐标系中描点、 连线 ,画出这两个函数的图象,如图所示 . 活动探究:思考以下问题.(小组讨论,3 min) 当自变量x取同一数值时,这两个函数的函数值之间有什么关系 反映在图象上 相应的两个点之间的位置又有什么关系 观察这两个函数的图象,分别说出它们的开口方向 ,对称轴和顶点坐标,它们有哪些是相同的 又有哪些不同? 当自变量x取同一数值时,函数 的值都比函数 的值大1.反映在图象上,函数 的图象上的每一个点都在函数 的图象上相应点的上方一个单位. 当x 时,函数值y随x的增大而减小; 当x 时,函数值y随x的增大而增大; 当x 时,函数取得最 值,最 值y= . 函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的图象形状 ,只是位置不同;当c>0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到,当c<0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到. 巩固练习 思考以下问题,小组讨论,3 min.用描点法画二次函数的图象 在平面直角坐标系中描点,然后用光滑的曲线顺次连接各点,得到函数的图象. 当自变量x取同一数值时,这两个函数的函数值之间有什么关系 反映在图象上 相应的两个点之间的位置又有什么关系 教师再给予点评、引导,然后共同完成问题的解决. 在探索中发现,这样才能理解其中的规律并能加以总结 通过本环节的讲解与训练,让学生对利用新知识解决一些简单问题有更加明确的认识,同时也尽量让学生明白知识点不是孤立的,需要前后联系,才能更好地处理一些新问题. 加强学生的合作意识,使学生养成大胆猜测和想象的能力,积极参与数学问题的谈论,敢于发表自己的见解 当c>0时,y=ax2+c的图象可由y=ax2的图象向上平移 c个单位得到,当c<0时,函数y=ax2+c的图象可由y=ax2的图象向 下平移 |c|个单位得到.
课堂小结 引导学生自己小结本节课的知识要点及数学方法. 将本节知识点进行很好的回顾以加深学生的印象,同时使知识系统化.
1
课题 26.2.2 二次函数y=ax2+bx+c的图象和性质 单元 第26章 学科 数学 年级 九年级
学习 目标 1.熟练画出二次函数y=ax2+c 的函数图象. 2.掌握并能够正确运用二次函数y=ax2+c 的特点与性质.
重点 运用二次函数y=ax2+c 的特点与性质.
难点 掌握并能够正确运用二次函数y=ax2+c 的特点与性质.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 复习引入 这个函数的图象是如何画出来的 复习之前内容,激发学生的兴趣,引入本节课所学内容. 复习旧知识,引入新课,激发学生的学习兴趣.
讲授新课 活动探究:思考以下问题,动手画一画.(小组讨论,3 min) 试研究二次函数的图象 分析 将函数关系式配方,得 我们设法寻求它与函数 的联系.为此,先看几个简单的例子. 例2:在同一个平面直角坐标系中,画出下列函数与的图象. 解:列表 在平面直角坐标系中描点、 连线 ,画出这两个函数的图象,如图所示 . 活动探究:思考以下问题.(小组讨论,3 min) 当自变量x取同一数值时,这两个函数的函数值之间有什么关系 反映在图象上 相应的两个点之间的位置又有什么关系 观察这两个函数的图象,分别说出它们的开口方向 ,对称轴和顶点坐标,它们有哪些是相同的 又有哪些不同? 当自变量x取同一数值时,函数 的值都比函数 的值大1.反映在图象上,函数 的图象上的每一个点都在函数 的图象上相应点的上方一个单位. 当x 时,函数值y随x的增大而减小; 当x 时,函数值y随x的增大而增大; 当x 时,函数取得最 值,最 值y= . 函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的图象形状 ,只是位置不同;当c>0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到,当c<0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到. 巩固练习 思考以下问题,小组讨论,3 min.用描点法画二次函数的图象 在平面直角坐标系中描点,然后用光滑的曲线顺次连接各点,得到函数的图象. 当自变量x取同一数值时,这两个函数的函数值之间有什么关系 反映在图象上 相应的两个点之间的位置又有什么关系 教师再给予点评、引导,然后共同完成问题的解决. 在探索中发现,这样才能理解其中的规律并能加以总结 通过本环节的讲解与训练,让学生对利用新知识解决一些简单问题有更加明确的认识,同时也尽量让学生明白知识点不是孤立的,需要前后联系,才能更好地处理一些新问题. 加强学生的合作意识,使学生养成大胆猜测和想象的能力,积极参与数学问题的谈论,敢于发表自己的见解 当c>0时,y=ax2+c的图象可由y=ax2的图象向上平移 c个单位得到,当c<0时,函数y=ax2+c的图象可由y=ax2的图象向 下平移 |c|个单位得到.
课堂小结 引导学生自己小结本节课的知识要点及数学方法. 将本节知识点进行很好的回顾以加深学生的印象,同时使知识系统化.
1
