2.5 直角三角形（1)说课课件

课件19张PPT。2.5 直角三角形（1）许巷中学 於国栋一、教材分析：1、教材的地位和作用： 本节课是在上节学习了等边三角形之后，继续学习的一种特殊三角形——直角三角形，是初中几何学习中的重要内容之一，是今后判断某个三角形是直角三角形的重要方法之一，在以后的解题中，将有十分广泛的应用，所以本节在本章中是重要内容之一。2、教材的重、难点：难点：本节例2涉及的知识点较多，推理表述较长。 重点：直角三角形的两个锐角互余的性质及其应用。 二、教学目标
根据新课程标准和本节内容在整个初中数学中的地位与作用，我从以下三个方面制定了本节课的教学目标：1、知识与技能目标：理解直角三角形的性质，知道怎样
判定一个直角三角形是直角三角形，能够运用直角三角形
的性质和判定来解决有关问题。2、过程与方法目标：经过实际操作、独立思考、沟通交
流的学习过程，发展学生的思维，培养学生观察分析能力、
判断能力以及对数学的应用能力和创新能力。3、情感态度与价值观目标：培养学生敢于面对挑战和勇
于克服困难的意志，鼓励学生大胆尝试，从中获得成功的
体验，激发学生的学习热情。三、教法与学法1、教学方法：
（1）复习引入法：回顾学生已经熟悉的知识，以学生感兴趣的，并容易理解的问题为开端，让学生轻松、愉快地回答老师提出的问题后，带着成功的喜悦进入新课的学习。
（2）师生互动的探究教学法：充分给学生提供交流与归纳的空间，使整个数学活动生动活泼和富有个性的学习过程。 2、学法指导：
根据新课程理念，结合学生自身年龄特点和思维特点，主
要是要求和引导学生采用实践探索的方法，进而培养学生数
学学习的良好习惯，渗透终身学习的意识，培养学生们的创新
精神，使他们体会到数学问题解决的严密性和规范性。回顾1.三角形内角和为度.2.有 边相等的三角形叫做等腰三角
形;在同一个三角形中,等边对3.在△ABC中，若∠C=90度,则∠A+∠B=180两等角度.90四、教学过程锐角三角形
直角三角形
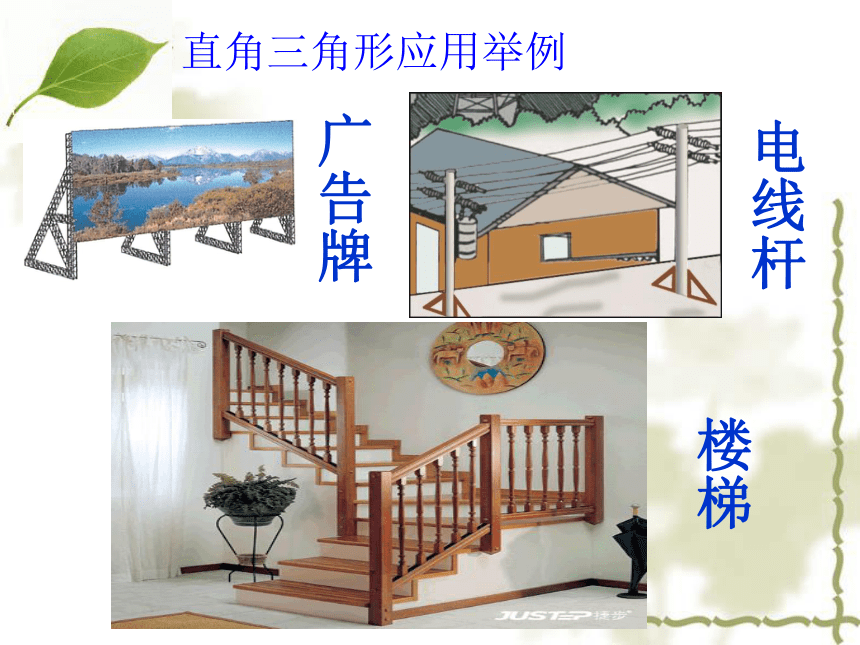
钝角三角形——有一个角是钝角。三角形按角的分类三角形——三个角都是锐角。——有一个角是直角。 你能举出生活中用到直角三角形的例子吗?直角三角形直角三角形应用举例广告牌电线杆楼梯定义 :有一个角是直角的三角形叫做 三角形。表示方法直角三角形用符号 Rt△ 表示，如图所示的三角形可记Rt△ABC,其中边AB叫做斜边，BC，AC叫做
直角边 。直角边直角边斜边直角直角三角形的性质 ACB从角看： ∠C=90° ， ∠A+∠B=90°怎样来判断一个三角形是直角三角形？ 从角看： ∠C=90° 或 ∠A+∠B=90° 直角三角形的两个锐角互余. 反过来，有两个角互余的三角形是直角三角形.上图中的三角板所表示的三角形有什么特征？
（从边、角方面去说明）等腰直角三角形两条直角边相等的直角三角形叫做等腰直角三角形。ACB它有什么性质呢？1）具有等腰三角形的所有性质
2）具有直角三角形的所有性质∠C=90°，∠A=∠B=45° 练习一：
1 Rt△ABC中，∠C=90°,∠B=28°，
则∠A=_______.
2 若∠C =∠A+∠B, 则△ABC是____
三角形.
在△ABC中，∠A=90°, ∠B=2∠C,
求∠B，∠C的度数。62 °直角例1 如图，CD是Rt△ABC斜边上的高。
（1）请找出图中各对互余的角。12（2）请找出图中各对相等的角。∵Rt△ABC，CD⊥AB，
∴∠1=∠B，∠2=∠A。例2 如图，在等腰直角三角形ABC中，AD是斜边BC上的高，则AD=BD=CD。请说明理由。D练习二在△ABC中，AD⊥BC,∠1=∠B,试说明△ABC为直角三角形
。ＢＣＡＤ１解：∵ AD⊥BC∴∠１＋∠Ｃ＝900∵ ∠1=∠B∴∠B ＋∠Ｃ＝900
∴∠BAC=1800-(∠B ＋∠Ｃ)=900∴△ABC为直角三角形。
1、认识直角三角形.
2、直角三角形的性质
直角三角形的两个锐角互余. 反过来，有两个角互余的三角形是直角三角形.
3、两条直角边相等的直角三角形叫做等腰直角三角形.收获五、板书设计2.5 直角三角形（1）一、直角三角形的定义：有一个角是直角的三角形。直角三角形的两个锐角互余。反过来，有两个角互余的三角形是直角三角形。二、例1：如图，CD是Rt⊿ABC斜边上的高,
请找出图中各对互余的角. 例2　如图，在等腰直角三角形ABC中,
AD是斜边BC上的高，则AD＝BD＝CD.
请说明理由。解：∵⊿ABC是Rt⊿.
∴∠A+∠B＝90°
∵CD⊥AB（已知）
∴⊿ACD，⊿BCD是Rt.⊿
∴∠A+ACD＝90°，∠B+∠BCD＝90°
∵∠ACB＝Rt∠，
∴∠ACD+∠BCD＝90°.
∴图中一共有4对互余的角，分别是
∠A与∠B；∠A与∠ACD，
∠B与∠BCD　∠ACD与∠BCD.（1）已知，如例2图，AD＝BD＝CD，
AD是斜边BC上的高，则AB＝AC.
请说明理由。
（2）已知，如例2图，AD＝BD＝CD,
∠B＝45°,则⊿ABC是等腰直角三角形.
请说明理由.变式六、设计说明 1、新课程大力提倡学生主动参与、乐于探究、勤于动手
的学习方式，我在教学设计过程中注意把学生的活动设
计放在首位，把知识的教学融于活动中，大胆放手，给
学生足够的时间和空间，动手实践，动脑思考。2.为学生提供思考、尝试、探索和发现的机会，使学生以一个创造者或发明者的身份去探究知识，从而形成学生主动参与、自觉实践的氛围。谢谢!
再见!