5.2函数（一）课件

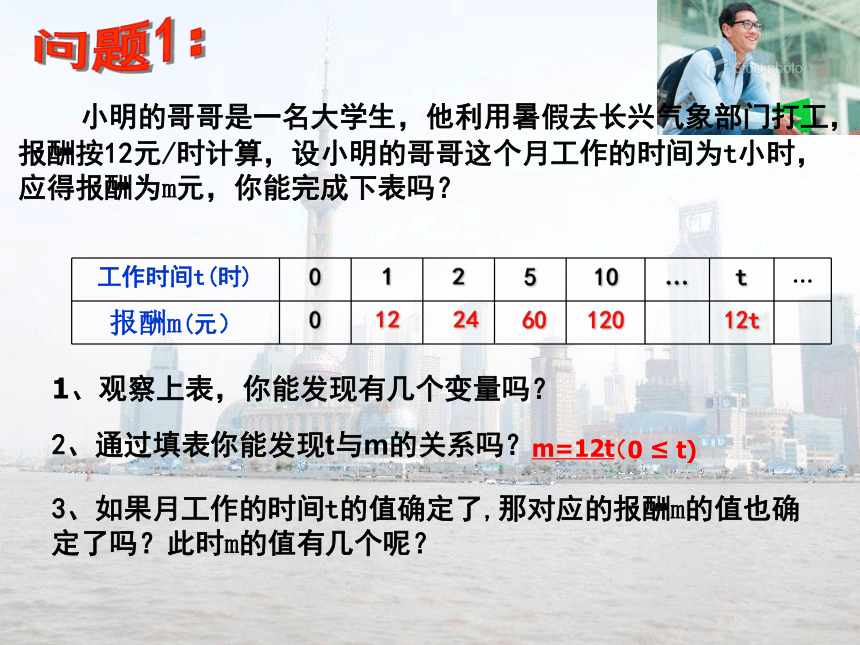
课件19张PPT。5.2函数 2、通过填表你能发现t与m的关系吗？122460120问题1： 小明的哥哥是一名大学生，他利用暑假去长兴气象部门打工，报酬按12元/时计算，设小明的哥哥这个月工作的时间为t小时，应得报酬为m元，你能完成下表吗？1、观察上表，你能发现有几个变量吗？3、如果月工作的时间t的值确定了,那对应的报酬m的值也确定了吗？此时m的值有几个呢？m=12t（0 ≤ t)12t问题2：1、在上图表示的变化过程中，有几个变量？
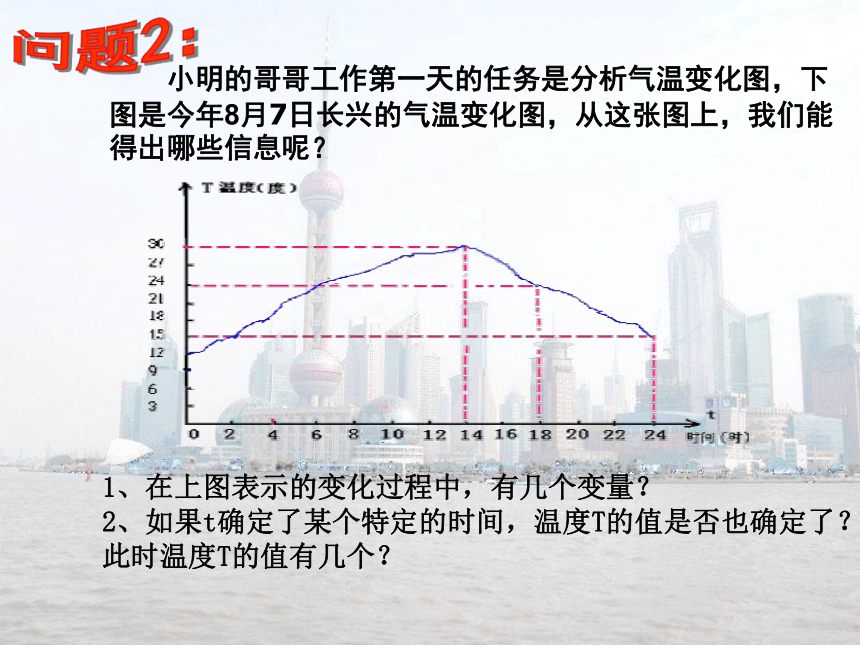
2、如果t确定了某个特定的时间，温度T的值是否也确定了？此时温度T的值有几个？　　小明的哥哥工作第一天的任务是分析气温变化图，下图是今年8月7日长兴的气温变化图，从这张图上，我们能得出哪些信息呢？　　长兴某建筑材料公司为气象局新的楼房建设提供部分材料。 设每吨材料售价为a(元),该公司的月利润为w(万元).
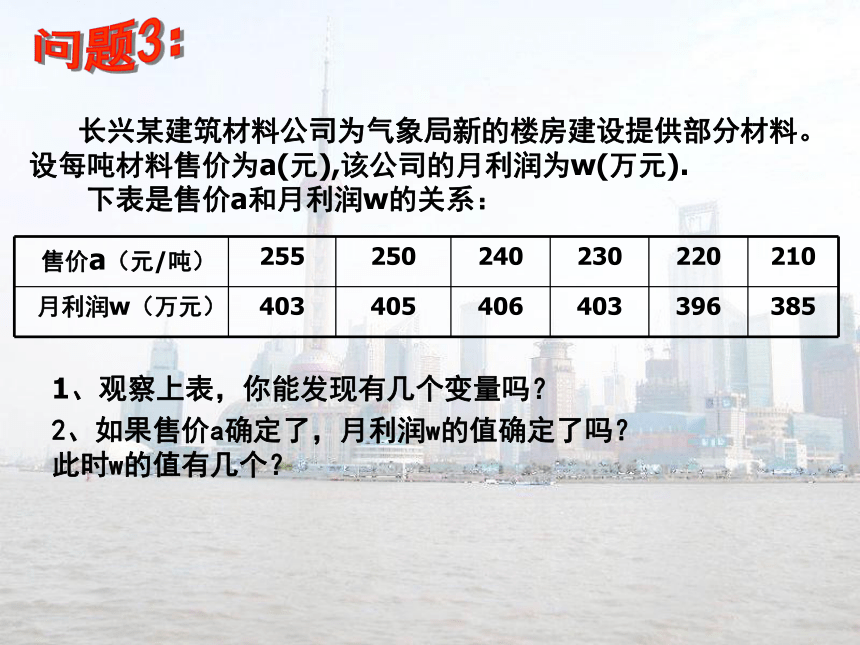
　　下表是售价a和月利润w的关系：1、观察上表，你能发现有几个变量吗？2、如果售价a确定了，月利润w的值确定了吗？
此时w的值有几个？问题3：
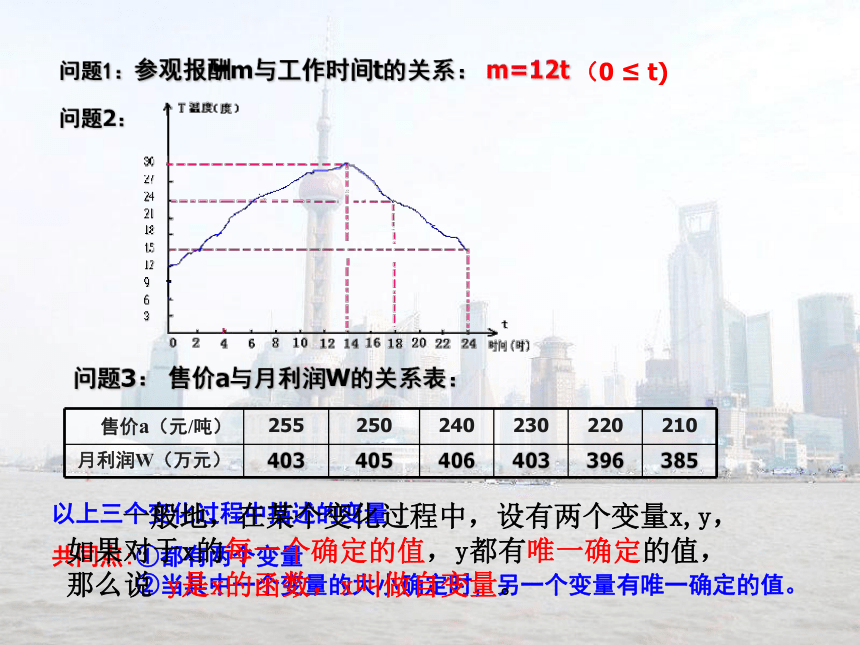
问题1：参观报酬m与工作时间t的关系： m=12t
问题2：问题3： 售价a与月利润W的关系表： 一般地，在某个变化过程中，设有两个变量x,y，
如果对于x的每一个确定的值，y都有唯一确定的值，
那么说 y是x的函数，x叫做自变量。
（0 ≤ t)
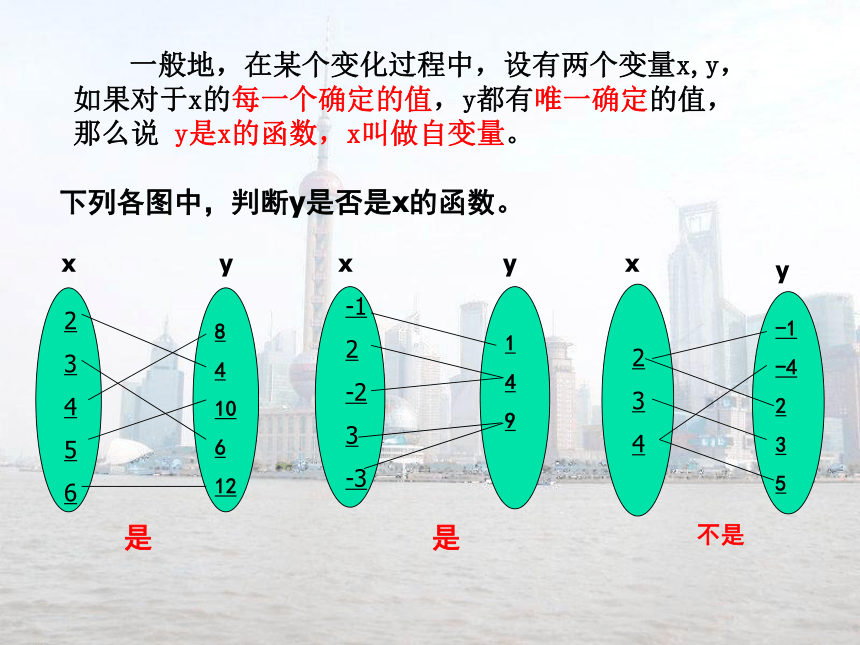
一般地，在某个变化过程中，设有两个变量x,y，
如果对于x的每一个确定的值，y都有唯一确定的值，
那么说 y是x的函数，x叫做自变量。
下列各图中，判断y是否是x的函数。是是不是
我们可以用哪些方法来表示函数呢？函数的常用表示方法：解析法，图象法，列表法问题1：报酬m与工作时间t的关系： m=12t
问题2：问题3： 售价a与月利润W的关系表：代一代画一画查一查一展身手 例1：长兴居民生活用电电费价格将定为0.53元/度，
设用电量是x度，应付电费y元.
（1）求y关于x的函数解析式.
（2）当x=10时，函数值是多少？
(3) 当y=53时，自变量x的值为多少？0.20.2增大0.1元展示自我　　某市市民用水费的价格是1.4元/立方米。设用水量为 n 立方米,应付水费为m元.在这个问题中,m关于n的函数解析式是________.当 n=5时,函数值是________,这一函数值的实际意义是______________________________________.7用水量为5立方米,应付水费用7元m=1.4n 观察下表反映的数据，y是x的函数吗？ 。
你的理由是 　　　　。不是对于x每一个确定的值，y的值不唯一确定 一个三角形的两边长分别为3，5，设第三边为x，周长为y。
(1)写出y与x的函数关系式________________(2)其中自变量x取值范围是什么？2＜x＜8 儿子学成今日返，老父早早到车站，
儿子到后细端详，父子高兴把家还．
如果用纵轴y表示父亲与儿子行进中离家的距离，用横轴x表示父亲离家的时间，那么下面的图象与上述诗的含义大致吻合的是 （　　） C (1)y是m的函数吗？为什么？解:（1）是，因为对于每个确定的m值，y都有唯一确定的值. 在国内投寄平信应付邮资如下表： (2)分别求当m=5,10,30,50时的函数值。（2）当m=5时，函数y的值是0.80元。当m=10时，函数y的值是0.80元。当m=30时，函数y的值是1.60元。当m=50时，函数y的值是2.40元。1.小明哥哥家住长兴，星期六上午9时骑自行车离开家去学校，途中休 息半小时，15时回到家，他有意描绘了离家的距离与
时间的变化情况.合作学习，共同提高（5）他由学校返回到家的平均速度是多少？（1） 10时和13时，他分别离 家多远？（2）小明休息时离家多远？（3）他到达学校是什么时间？学校离家多远？（4）11时到12时他行驶了多少千米？ 2.如图,正方形ABCD的边长为16，M为CD上的 一个动点，CM=x。（1）请写出△ADM的面积y关于x的函数关系式。（2）求出自变量x的取值范围。（3）当x取多少时，△ADM的面积为64？超越自我ABCD（M）x16-xM　这节课你学到了哪些新知识？说一说.畅所欲言：1、函数
　　一般地，在某个变化过程中，设有两个变量x,y，
如果对于x的每一个确定的值，y都有唯一确定的值，
那么说y 是x的函数，x叫做自变量。
代一代查一查画一画再 见