不等式的基本性质
图片预览

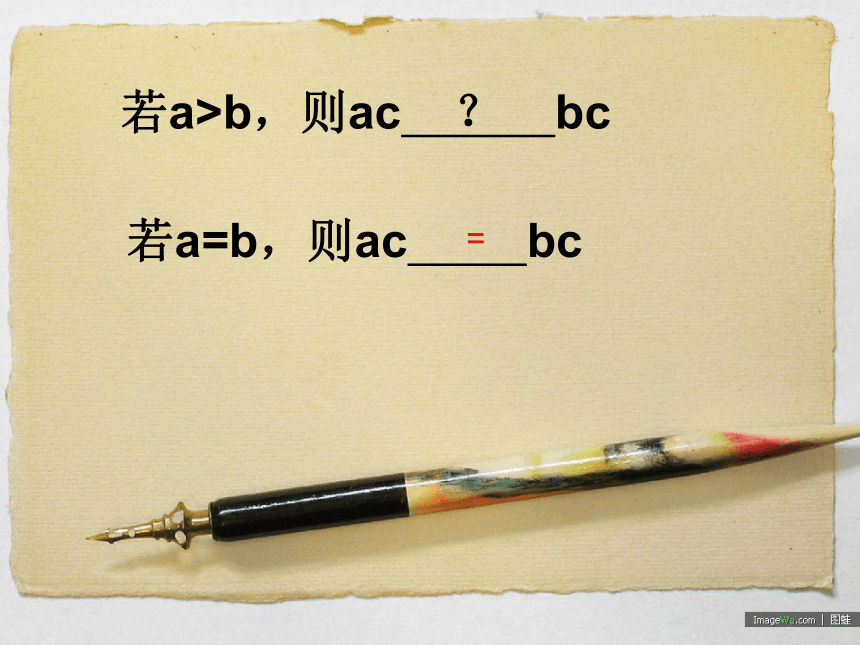


文档简介
课件12张PPT。若a>b,则ac ? bc
若a=b,则ac bc
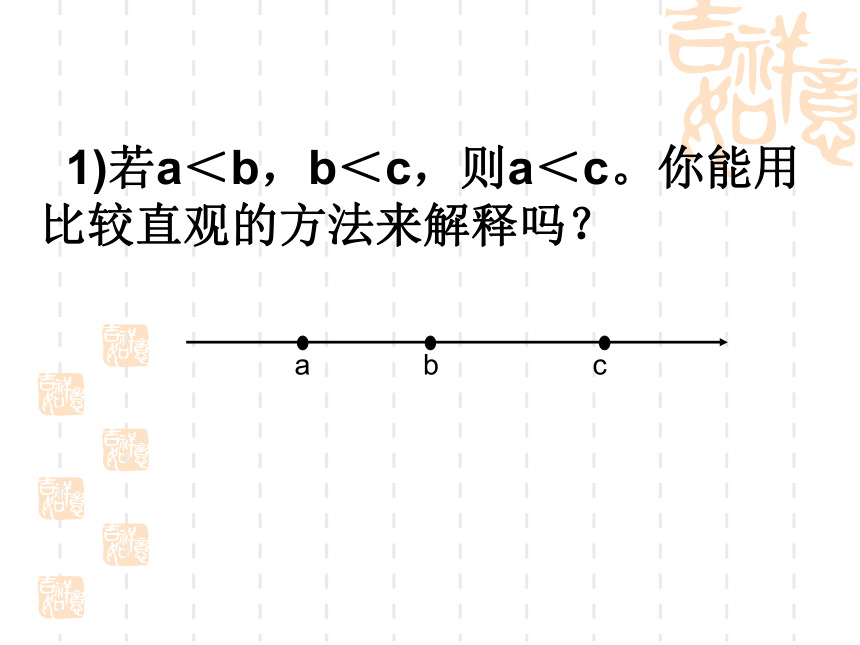
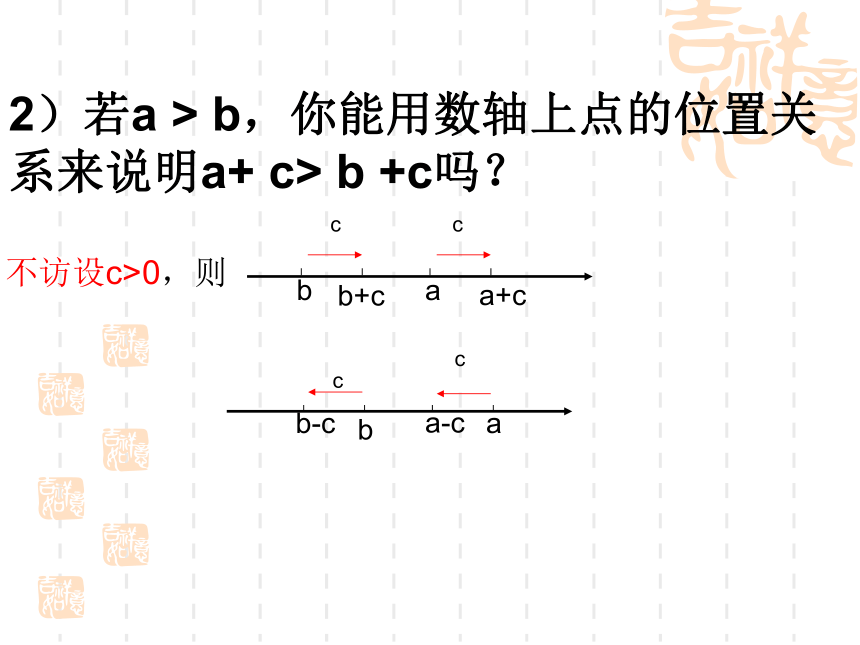
=§5.2不等式的基本性质 1)若a<b,b<c,则a<c。你能用比较直观的方法来解释吗?abc不访设c>0,则abb+ca+ccc2)若a > b,你能用数轴上点的位置关系来说明a+ c> b +c吗?
abb-ca-ccc3、填空,用“<、>、=“完成下列填空
1)由2<3 2)由4 <5
则2×5 3×5 则4×(-7) 5× (-7)
2÷5 3÷5 4÷(-7) 5 ÷(-7)
1)仔细观察两组数据有何变化?3)第一组不等号的方向没变,为什么第二组不等号的方向改变了呢?2)这两组不等式的变形有什么不同?<<>>2)不等式的两边都乘以零, 不等式不成立.
(不能除以零)注意:
1)不等式的两边都乘(或都除以)同一个负数, 必须改变不等号的方向。
1) 已知a > b,用不等号填空,并说明理由。则
2a 2 b (理由: )
2a+1 2b+1 (理由: )
-a -b (理由: )
5-3a 5-3b (理由: )小试牛刀:<<>不等式性质3不等式性质2、3不等式性质3不等式性质2、 3>2)下列各题是否正确?请说明理由
① 若a>b,则a-b>0
②如果ax>b且a≠0,那么x>
解:不正确, 两边都都除以同一个正数, 不等号不变;
两边都乘都除以同 一个负数,必须改变不等号的方向.
解:正确,两边同时减去一个数,所得的不等式仍然成立。数轴表示法
解:在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a典型例题:
已知a<0 ,试比较2a与a的大小。已知:不等式(a-2)x>a-2,得x<1, 求a 的取值范围?变式拓展:解:∵ (a-2)x>a-2 , x<1 ∴a-2 <0
∴a <-2
小结反思②若a >b,则ac>bc这种变形对吗?为什么?
①∵a+2>b,∴a>b-2这种变形对吗?
为什么?你能根据所学的知识来解释吗?再见!
若a=b,则ac bc
=§5.2不等式的基本性质 1)若a<b,b<c,则a<c。你能用比较直观的方法来解释吗?abc不访设c>0,则abb+ca+ccc2)若a > b,你能用数轴上点的位置关系来说明a+ c> b +c吗?
abb-ca-ccc3、填空,用“<、>、=“完成下列填空
1)由2<3 2)由4 <5
则2×5 3×5 则4×(-7) 5× (-7)
2÷5 3÷5 4÷(-7) 5 ÷(-7)
1)仔细观察两组数据有何变化?3)第一组不等号的方向没变,为什么第二组不等号的方向改变了呢?2)这两组不等式的变形有什么不同?<<>>2)不等式的两边都乘以零, 不等式不成立.
(不能除以零)注意:
1)不等式的两边都乘(或都除以)同一个负数, 必须改变不等号的方向。
1) 已知a > b,用不等号填空,并说明理由。则
2a 2 b (理由: )
2a+1 2b+1 (理由: )
-a -b (理由: )
5-3a 5-3b (理由: )小试牛刀:<<>不等式性质3不等式性质2、3不等式性质3不等式性质2、 3>2)下列各题是否正确?请说明理由
① 若a>b,则a-b>0
②如果ax>b且a≠0,那么x>
解:不正确, 两边都都除以同一个正数, 不等号不变;
两边都乘都除以同 一个负数,必须改变不等号的方向.
解:正确,两边同时减去一个数,所得的不等式仍然成立。数轴表示法
解:在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a典型例题:
已知a<0 ,试比较2a与a的大小。已知:不等式(a-2)x>a-2,得x<1, 求a 的取值范围?变式拓展:解:∵ (a-2)x>a-2 , x<1 ∴a-2 <0
∴a <-2
小结反思②若a >b,则ac>bc这种变形对吗?为什么?
①∵a+2>b,∴a>b-2这种变形对吗?
为什么?你能根据所学的知识来解释吗?再见!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
