九年级数学下册试题 1.3 解直角三角形同步测试-浙教版(含答案)
文档属性
| 名称 | 九年级数学下册试题 1.3 解直角三角形同步测试-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 292.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 00:00:00 | ||
图片预览


文档简介
1.3 解直角三角形
一、单选题
1.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为( )
A. B. C. D.
2.如图,在量角器的圆心处下挂一铅锤,制作了一个简易测倾仪.量角器的0刻度线对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是( ).
A.30° B.40° C.50° D.60°
3.如图,有一斜坡的长米,坡角,则斜坡的铅垂高度为( ).
A. B. C. D.
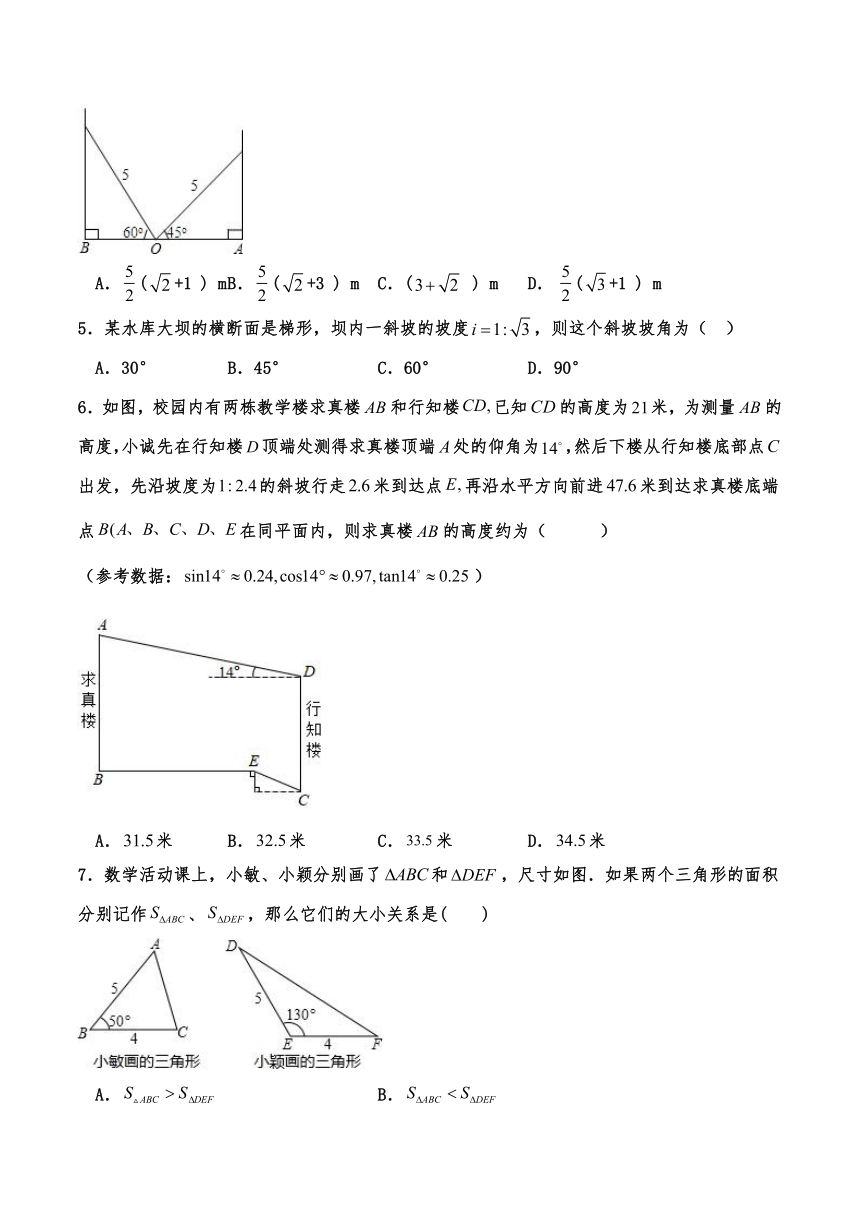
4.如图,学校的保管室有一架5m长的梯子斜靠在墙上,此时梯子与地面所成的角为45°如果梯子底端O固定不变,顶端靠到对面墙上,此时梯子与地面所成的角为60°,则此保管室的宽度AB为( )
A.(+1 ) m B.(+3 ) m C.( ) m D.(+1 ) m
5.某水库大坝的横断面是梯形,坝内一斜坡的坡度,则这个斜坡坡角为( )
A.30° B.45° C.60° D.90°
6.如图,校园内有两栋教学楼求真楼和行知楼已知的高度为米,为测量的高度,小诚先在行知楼顶端处测得求真楼顶端处的仰角为,然后下楼从行知楼底部点出发,先沿坡度为的斜坡行走米到达点再沿水平方向前进米到达求真楼底端点在同平面内,则求真楼的高度约为( )
(参考数据:)
A.米 B.米 C.米 D.米
7.数学活动课上,小敏、小颖分别画了和,尺寸如图.如果两个三角形的面积分别记作、,那么它们的大小关系是( )
A. B.
C. D.不能确定
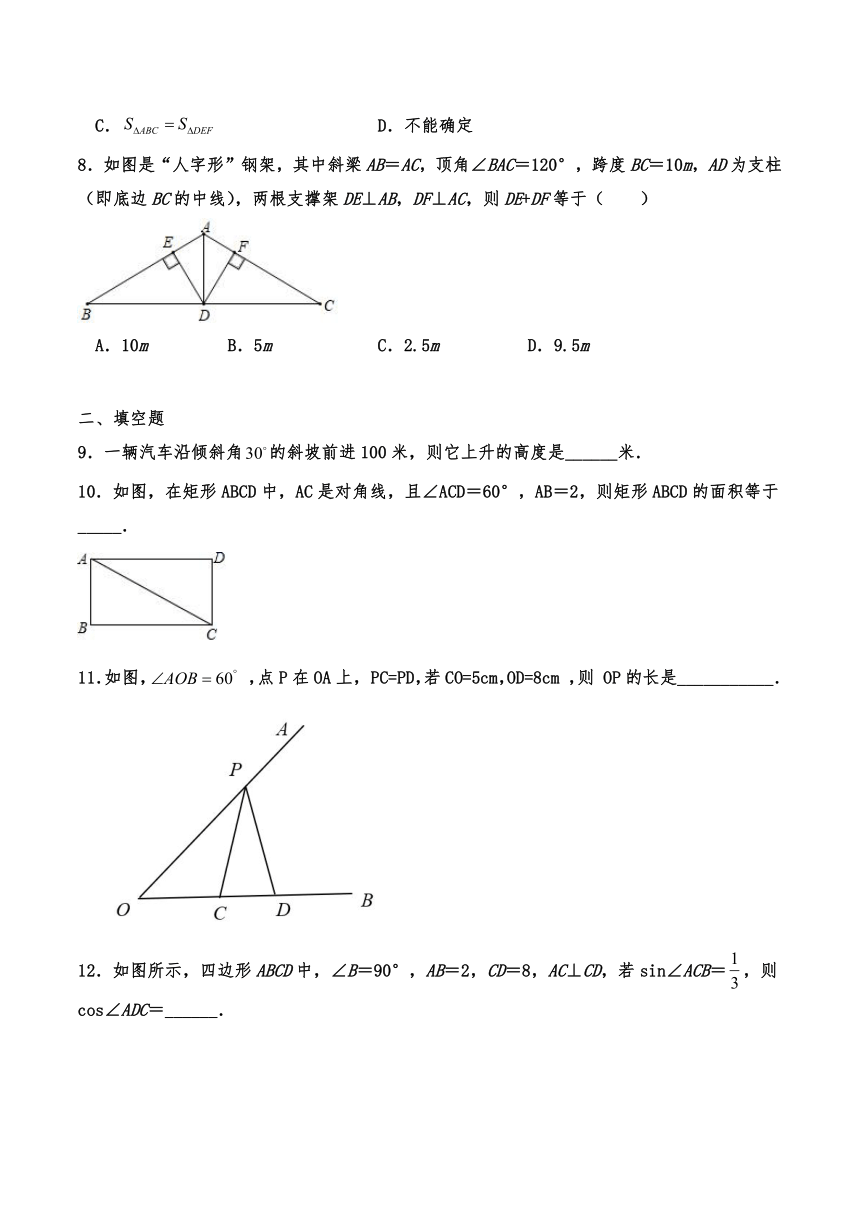
8.如图是“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为支柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF等于( )
A.10m B.5m C.2.5m D.9.5m
二、填空题
9.一辆汽车沿倾斜角的斜坡前进100米,则它上升的高度是______米.
10.如图,在矩形ABCD中,AC是对角线,且∠ACD=60°,AB=2,则矩形ABCD的面积等于_____.
11.如图, ,点P在OA上, PC=PD,若CO=5cm,OD=8cm ,则 OP的长是___________.
12.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=______.
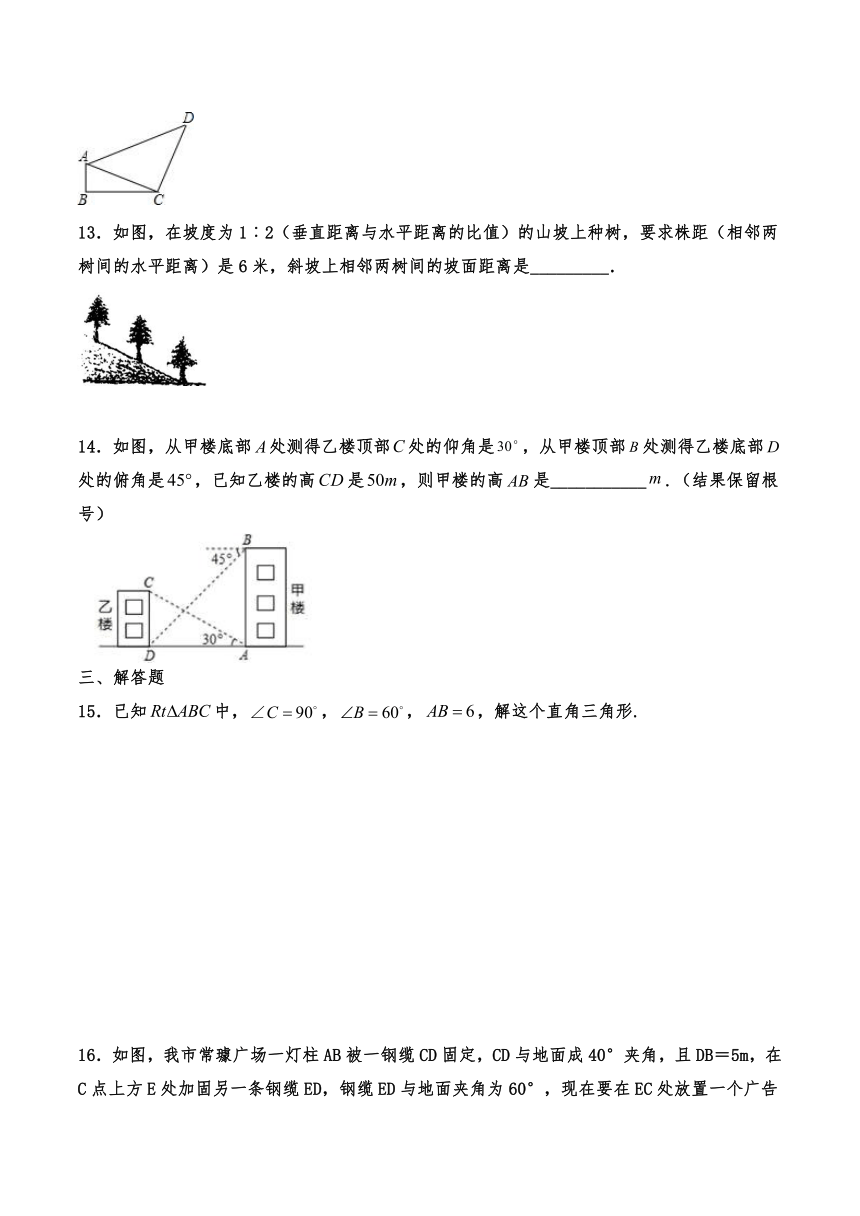
13.如图,在坡度为1︰2(垂直距离与水平距离的比值)的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是_________.
14.如图,从甲楼底部处测得乙楼顶部处的仰角是,从甲楼顶部处测得乙楼底部处的俯角是,已知乙楼的高是,则甲楼的高是___________.(结果保留根号)
三、解答题
15.已知中,,,,解这个直角三角形.
16.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
17.襄阳东站的建成运营标志者我市正式进入高铁时代,郑万高速铁路襄阳至万州段的建设也正在推进中.如图,工程队拟沿方向开山修路,为加快施工进度,需在小山的另一边点E处同时施工,要使A,C,E三点在一条直线上,工程队从上的一点B取,米,.那么点E与点D间的距离是多少米?(参考数据:,,)
18.如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:≈1.732)
19.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
20.如图,在边长为1个单位长度的小正方形组成的12×12的网格中,AB是以网络线的交点(格点)为端点的线段;
(1)将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段CD;
(2)以线段CD为一边,作一个菱形CDEF,连接DF,使,点E,F也为格点.
答案
一、单选题
B.B.C.A.A.B.C.B.
二、填空题
9.50.
10.4.
11.13cm.
12.
13.米.
14..
三、解答题
15.
解:在中,,,,
,
,
.
故答案为∠A=30°,BC=3,AC= .
16.
解:在Rt△CDB中,tan∠BDC=,
∴BC=BDtan40°≈4,
在Rt△BDE中,tan∠BDE=,
∴BE=BDtan∠BDE=5,
∴CE=BE﹣BC≈4.66(m),
答:广告牌EC的高度约为4.66m.
17.
解:∵,
∴,
∴,即,解得(米),
答:点E与点D间的距离是358.4米.
18.
解:如图,过点C作CD⊥AB于点D,
由题意可知:
∠DCA=60°,∠DCB=45°,AB=380,
∴在Rt△BCD中,CD=BD,
在Rt△ACD中,tan∠DCA=,
∴tan60°==,
∴CD=190+190≈519.1(米).
答:这条公路的长约为519.1米.
19.
解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
20.
(1)如图所示:线段CD即为所求;
(2)如图所示:菱形CDEF即为所求.
一、单选题
1.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为( )
A. B. C. D.
2.如图,在量角器的圆心处下挂一铅锤,制作了一个简易测倾仪.量角器的0刻度线对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是( ).
A.30° B.40° C.50° D.60°
3.如图,有一斜坡的长米,坡角,则斜坡的铅垂高度为( ).
A. B. C. D.
4.如图,学校的保管室有一架5m长的梯子斜靠在墙上,此时梯子与地面所成的角为45°如果梯子底端O固定不变,顶端靠到对面墙上,此时梯子与地面所成的角为60°,则此保管室的宽度AB为( )
A.(+1 ) m B.(+3 ) m C.( ) m D.(+1 ) m
5.某水库大坝的横断面是梯形,坝内一斜坡的坡度,则这个斜坡坡角为( )
A.30° B.45° C.60° D.90°
6.如图,校园内有两栋教学楼求真楼和行知楼已知的高度为米,为测量的高度,小诚先在行知楼顶端处测得求真楼顶端处的仰角为,然后下楼从行知楼底部点出发,先沿坡度为的斜坡行走米到达点再沿水平方向前进米到达求真楼底端点在同平面内,则求真楼的高度约为( )
(参考数据:)
A.米 B.米 C.米 D.米
7.数学活动课上,小敏、小颖分别画了和,尺寸如图.如果两个三角形的面积分别记作、,那么它们的大小关系是( )
A. B.
C. D.不能确定
8.如图是“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为支柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF等于( )
A.10m B.5m C.2.5m D.9.5m
二、填空题
9.一辆汽车沿倾斜角的斜坡前进100米,则它上升的高度是______米.
10.如图,在矩形ABCD中,AC是对角线,且∠ACD=60°,AB=2,则矩形ABCD的面积等于_____.
11.如图, ,点P在OA上, PC=PD,若CO=5cm,OD=8cm ,则 OP的长是___________.
12.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=______.
13.如图,在坡度为1︰2(垂直距离与水平距离的比值)的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是_________.
14.如图,从甲楼底部处测得乙楼顶部处的仰角是,从甲楼顶部处测得乙楼底部处的俯角是,已知乙楼的高是,则甲楼的高是___________.(结果保留根号)
三、解答题
15.已知中,,,,解这个直角三角形.
16.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
17.襄阳东站的建成运营标志者我市正式进入高铁时代,郑万高速铁路襄阳至万州段的建设也正在推进中.如图,工程队拟沿方向开山修路,为加快施工进度,需在小山的另一边点E处同时施工,要使A,C,E三点在一条直线上,工程队从上的一点B取,米,.那么点E与点D间的距离是多少米?(参考数据:,,)
18.如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:≈1.732)
19.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
20.如图,在边长为1个单位长度的小正方形组成的12×12的网格中,AB是以网络线的交点(格点)为端点的线段;
(1)将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段CD;
(2)以线段CD为一边,作一个菱形CDEF,连接DF,使,点E,F也为格点.
答案
一、单选题
B.B.C.A.A.B.C.B.
二、填空题
9.50.
10.4.
11.13cm.
12.
13.米.
14..
三、解答题
15.
解:在中,,,,
,
,
.
故答案为∠A=30°,BC=3,AC= .
16.
解:在Rt△CDB中,tan∠BDC=,
∴BC=BDtan40°≈4,
在Rt△BDE中,tan∠BDE=,
∴BE=BDtan∠BDE=5,
∴CE=BE﹣BC≈4.66(m),
答:广告牌EC的高度约为4.66m.
17.
解:∵,
∴,
∴,即,解得(米),
答:点E与点D间的距离是358.4米.
18.
解:如图,过点C作CD⊥AB于点D,
由题意可知:
∠DCA=60°,∠DCB=45°,AB=380,
∴在Rt△BCD中,CD=BD,
在Rt△ACD中,tan∠DCA=,
∴tan60°==,
∴CD=190+190≈519.1(米).
答:这条公路的长约为519.1米.
19.
解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
20.
(1)如图所示:线段CD即为所求;
(2)如图所示:菱形CDEF即为所求.
