九年级数学下册试题 2.2 切线长定理同步测试-浙教版(含答案)
文档属性
| 名称 | 九年级数学下册试题 2.2 切线长定理同步测试-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 536.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 20:34:17 | ||
图片预览


文档简介
2.2 切线长定理
一、单选题
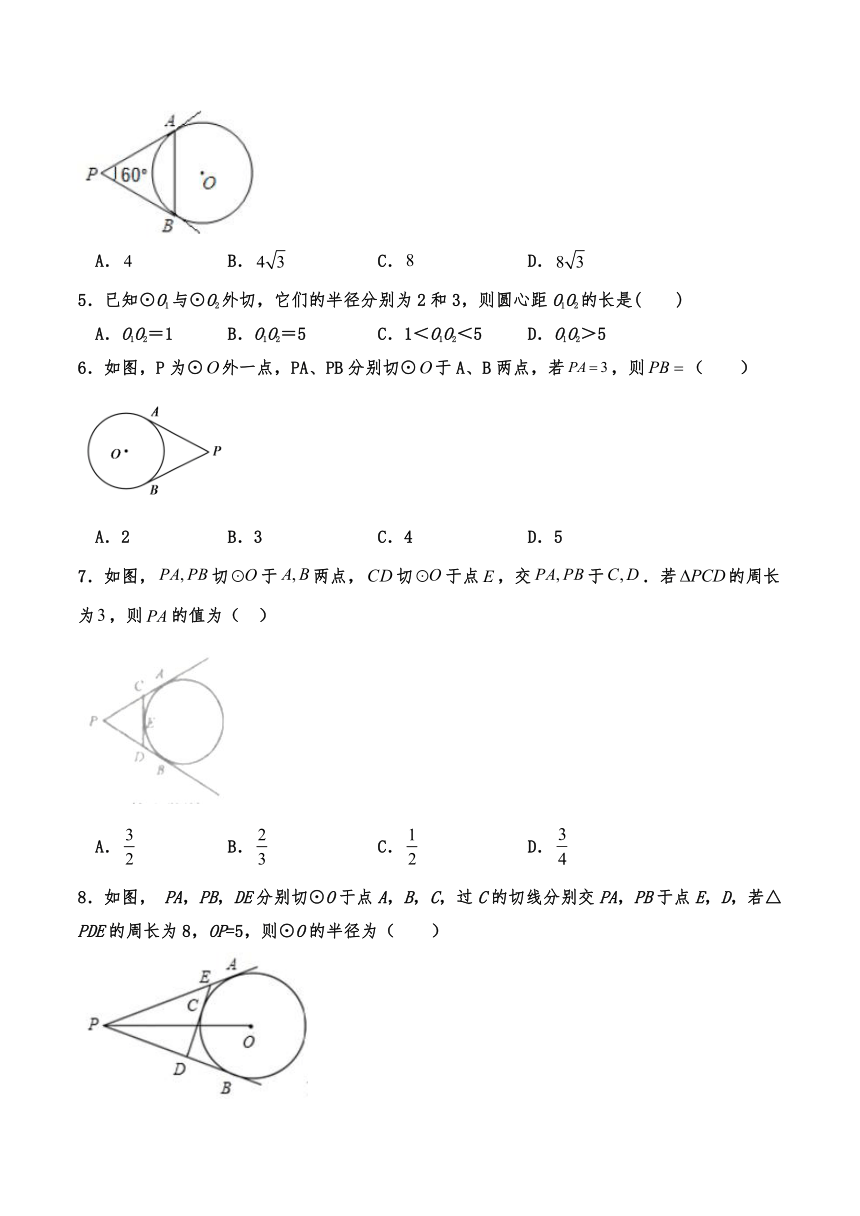
1.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( )
A. B. C. D.
2.如图,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是弧AB上任意一点,过点C作⊙O的切线分别交PA,PB于点D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
3.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,则∠P的度数是( )
A.50° B.60° C.70° D.80°
4.如图,从圆外一点引圆的两条切线,,切点分别为,,如果, ,那么弦AB的长是( )
A. B. C. D.
5.已知⊙O1与⊙O2外切,它们的半径分别为2和3,则圆心距O1O2的长是( )
A.O1O2=1 B.O1O2=5 C.1<O1O2<5 D.O1O2>5
6.如图,P为⊙外一点,PA、PB分别切⊙于A、B两点,若,则( )
A.2 B.3 C.4 D.5
7.如图,切于两点,切于点,交于.若的周长为,则的值为( )
A. B. C. D.
8.如图, PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若△PDE的周长为8,OP=5,则⊙O的半径为( )
A.2 B.3 C.4 D.不能确定
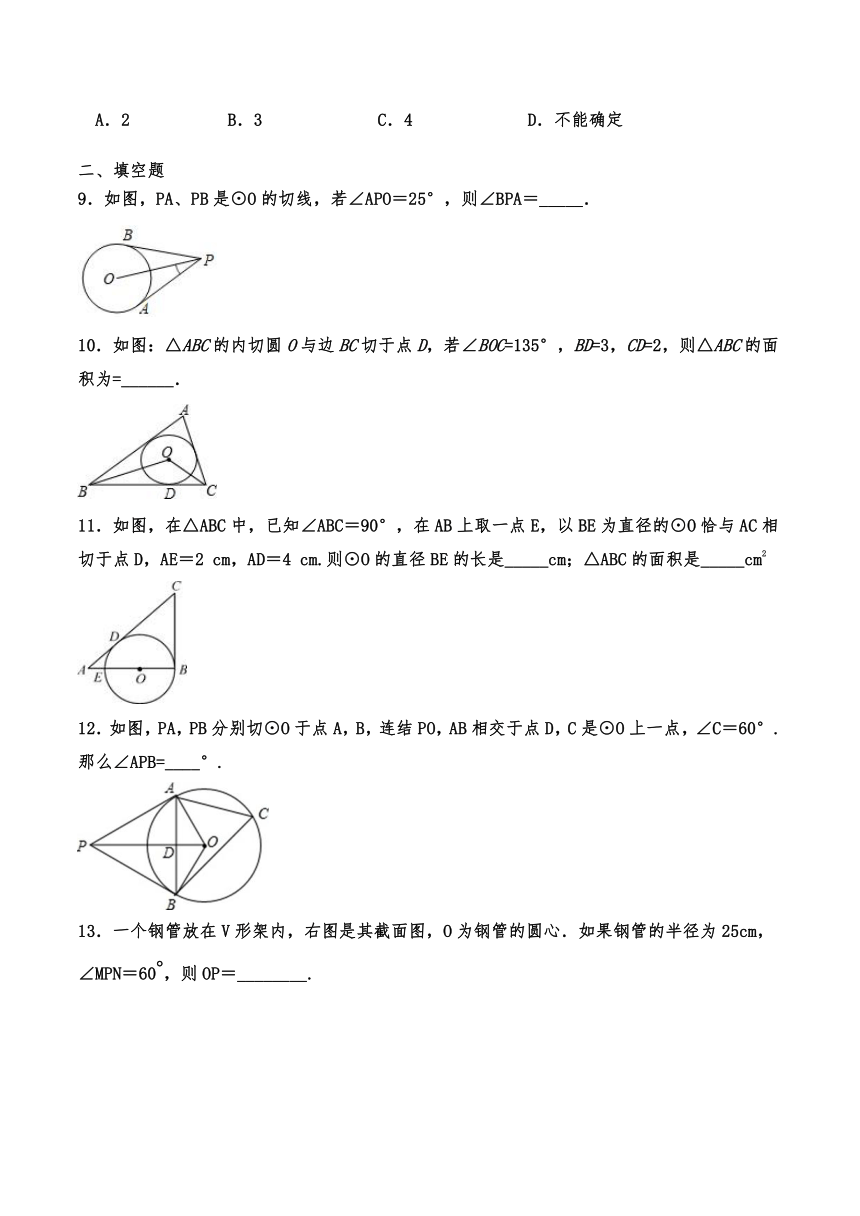
二、填空题
9.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=_____.
10.如图:△ABC的内切圆O与边BC切于点D,若∠BOC=135°,BD=3,CD=2,则△ABC的面积为=______.
11.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,AE=2 cm,AD=4 cm.则⊙O的直径BE的长是_____cm;△ABC的面积是_____cm2
12.如图,PA,PB分别切⊙O于点A,B,连结PO,AB相交于点D,C是⊙O上一点,∠C=60°. 那么∠APB=____°.
13.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25cm,∠MPN=60,则OP=________.
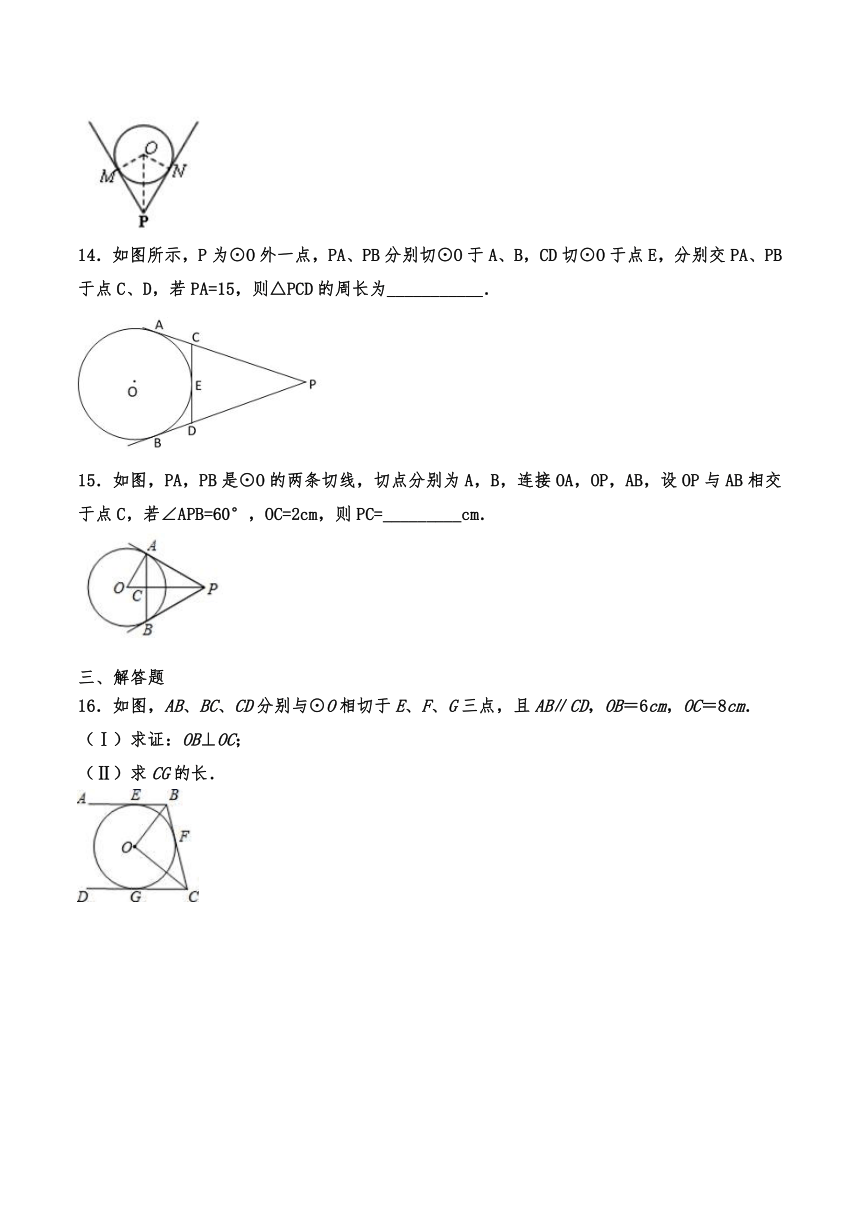
14.如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为___________.
15.如图,PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OP,AB,设OP与AB相交于点C,若∠APB=60°,OC=2cm,则PC=_________cm.
三、解答题
16.如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(Ⅰ)求证:OB⊥OC;
(Ⅱ)求CG的长.
17.如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
18.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
19.如图,是直角三角形,,以为直径的与边交于点,过作的切线交于,连接,交于.
(1)求证:;
(2)若,,求线段的长.
20.如图,在中,,是线段上一点,以为圆心,为半径作,与相切于点,直线交于点,.
(1)求证:是的角平分线;
(2)若,求的值;
(3)如图,在(2)条件下,连接交于点,的半径为3,求的长.
答案
一、单选题
A .B.C.C.B.B.A.B.
二、填空题
9.50°
10.6.
11.6, 24
12.60
13.50cm
14.30
15.6
三、解答题
16.
解:(Ⅰ)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°,
∴OB⊥OC;
(Ⅱ)由(Ⅰ)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴ 即
∴OF=4.8cm.
∴ =6.4cm,
∵CF、CG分别与⊙O相切于F、G,
∴CG=CF=6.4cm.
17.
(1)连接OD,
∴OD⊥AC
∴△ODA是直角三角形
设半径为r
∴AO=r+2
∴
解之得:r=3
∴BE=6
(2)∵∠ABC=900
∴OB⊥BC
∴BC是⊙O的切线
∵CD切⊙O于D
∴CB=CD
令CB=x
∴AC=x+4, CB=x,AB=8
∵
∴x=6.
∴S△ABC=24(cm2).
故答案为:(1)BE=6;(2) S△ABC=24..
18.
证明:连接OD,
∵BC是和⊙O相切于点B的切线
∴∠CBO=90°.
∵AD平行于OC,
∴∠COD=∠ODA,∠COB=∠A;
∵∠ODA=∠A,
∴∠COD=∠COB,OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠CDO=∠CBO=90°.
∴DC是⊙O的切线.
19.
证明(1)方法一:连接交于,
∵且为直径
∴是的切线
又∵DE是的切线
∴,,
∴
∴
∵为直径
∴
∴
方法二:连接,
∵且为直径
∴是的切线
又∵是的切线
∴
∴
∵为直径
∴
∴
∴
∴
∴
∴
又∵
∴
(2)连接,
∵
∴
∵
∴
∴
∵
又∵,
∴
∴
∵
∴
∴
∴.
20.
(1)证明:连接,
与相切于点,
,
,,
,
即是的角平分线;
(2)如图2,连接,
是的直径,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(3)由(2)可知:,
设,,
,
,
,
,
解得:或(不合题意,舍去),
,,
,
如图3,连接交于点,
,是的切线,
,,
,
,
,
,
,
,
,
,
.
一、单选题
1.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( )
A. B. C. D.
2.如图,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是弧AB上任意一点,过点C作⊙O的切线分别交PA,PB于点D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
3.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,则∠P的度数是( )
A.50° B.60° C.70° D.80°
4.如图,从圆外一点引圆的两条切线,,切点分别为,,如果, ,那么弦AB的长是( )
A. B. C. D.
5.已知⊙O1与⊙O2外切,它们的半径分别为2和3,则圆心距O1O2的长是( )
A.O1O2=1 B.O1O2=5 C.1<O1O2<5 D.O1O2>5
6.如图,P为⊙外一点,PA、PB分别切⊙于A、B两点,若,则( )
A.2 B.3 C.4 D.5
7.如图,切于两点,切于点,交于.若的周长为,则的值为( )
A. B. C. D.
8.如图, PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若△PDE的周长为8,OP=5,则⊙O的半径为( )
A.2 B.3 C.4 D.不能确定
二、填空题
9.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=_____.
10.如图:△ABC的内切圆O与边BC切于点D,若∠BOC=135°,BD=3,CD=2,则△ABC的面积为=______.
11.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,AE=2 cm,AD=4 cm.则⊙O的直径BE的长是_____cm;△ABC的面积是_____cm2
12.如图,PA,PB分别切⊙O于点A,B,连结PO,AB相交于点D,C是⊙O上一点,∠C=60°. 那么∠APB=____°.
13.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25cm,∠MPN=60,则OP=________.
14.如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为___________.
15.如图,PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OP,AB,设OP与AB相交于点C,若∠APB=60°,OC=2cm,则PC=_________cm.
三、解答题
16.如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(Ⅰ)求证:OB⊥OC;
(Ⅱ)求CG的长.
17.如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
18.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
19.如图,是直角三角形,,以为直径的与边交于点,过作的切线交于,连接,交于.
(1)求证:;
(2)若,,求线段的长.
20.如图,在中,,是线段上一点,以为圆心,为半径作,与相切于点,直线交于点,.
(1)求证:是的角平分线;
(2)若,求的值;
(3)如图,在(2)条件下,连接交于点,的半径为3,求的长.
答案
一、单选题
A .B.C.C.B.B.A.B.
二、填空题
9.50°
10.6.
11.6, 24
12.60
13.50cm
14.30
15.6
三、解答题
16.
解:(Ⅰ)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°,
∴OB⊥OC;
(Ⅱ)由(Ⅰ)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴ 即
∴OF=4.8cm.
∴ =6.4cm,
∵CF、CG分别与⊙O相切于F、G,
∴CG=CF=6.4cm.
17.
(1)连接OD,
∴OD⊥AC
∴△ODA是直角三角形
设半径为r
∴AO=r+2
∴
解之得:r=3
∴BE=6
(2)∵∠ABC=900
∴OB⊥BC
∴BC是⊙O的切线
∵CD切⊙O于D
∴CB=CD
令CB=x
∴AC=x+4, CB=x,AB=8
∵
∴x=6.
∴S△ABC=24(cm2).
故答案为:(1)BE=6;(2) S△ABC=24..
18.
证明:连接OD,
∵BC是和⊙O相切于点B的切线
∴∠CBO=90°.
∵AD平行于OC,
∴∠COD=∠ODA,∠COB=∠A;
∵∠ODA=∠A,
∴∠COD=∠COB,OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠CDO=∠CBO=90°.
∴DC是⊙O的切线.
19.
证明(1)方法一:连接交于,
∵且为直径
∴是的切线
又∵DE是的切线
∴,,
∴
∴
∵为直径
∴
∴
方法二:连接,
∵且为直径
∴是的切线
又∵是的切线
∴
∴
∵为直径
∴
∴
∴
∴
∴
∴
又∵
∴
(2)连接,
∵
∴
∵
∴
∴
∵
又∵,
∴
∴
∵
∴
∴
∴.
20.
(1)证明:连接,
与相切于点,
,
,,
,
即是的角平分线;
(2)如图2,连接,
是的直径,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(3)由(2)可知:,
设,,
,
,
,
,
解得:或(不合题意,舍去),
,,
,
如图3,连接交于点,
,是的切线,
,,
,
,
,
,
,
,
,
,
.
