九年级数学下册试题 2.3 三角形的内切圆同步测试-浙教版(含答案)
文档属性
| 名称 | 九年级数学下册试题 2.3 三角形的内切圆同步测试-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 530.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 00:00:00 | ||
图片预览




文档简介
2.3 三角形的内切圆
一、单选题
1.如图,已知正方形ABCD的边长是8,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值是( )
A. B. C. D.
2.如图,在中,是直径,点是上一点,点是弧的中点,于点,过点的切线交的延长线于点,连接,分别交,于点.连接,关于下列结论:① ;②;③点是的外心,其中正确结论是( )
A.①② B.①③ C.②③ D.①②③
3.如图,把剪成三部分,边,,放在同一直线上,点都落在直线上,直线.在中,若,则的度数为( )
A. B. C. D.
4.一个等腰直角三角形的内切圆与外接圆的半径之比为( )
A. B. C. D.
5.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?“其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径”则该圆的直径为( )
A.6步 B.5步 C.4步 D.3步
6.下列关于三角形的内心说法正确的是( )
A.内心是三角形三条角平分线的交点
B.内心是三角形三边中垂线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )
A.128° B.126° C.122° D.120°
8.如图,的直径与弦的延长线交于点,若,,则=( )
A. B. C. D.
二、填空题
9.阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:求作:的内切圆.
小明的作法如下:如图2,
作,的平分线BE和CF,两线相交于点O;
过点O作,垂足为点D;
点O为圆心,OD长为半径作所以,即为所求作的圆.
请回答:该尺规作图的依据是______.
10.边长分别为3、4、5的三角形的内切圆半径与外接圆半径之比为________.
11.已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.
12.如图,已知点是的内心,若,则__________.
13.如图,在中,弦,点在上移动,连结,过点作交于点,则的最大值为__________.
14.在中,,若为的外心,则______度;若为的内心,则______度.
三、解答题
15.如图,点是外接圆的圆心,点是内切圆的圆心,已知,求和的度数.
16.如图所示,AB为☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
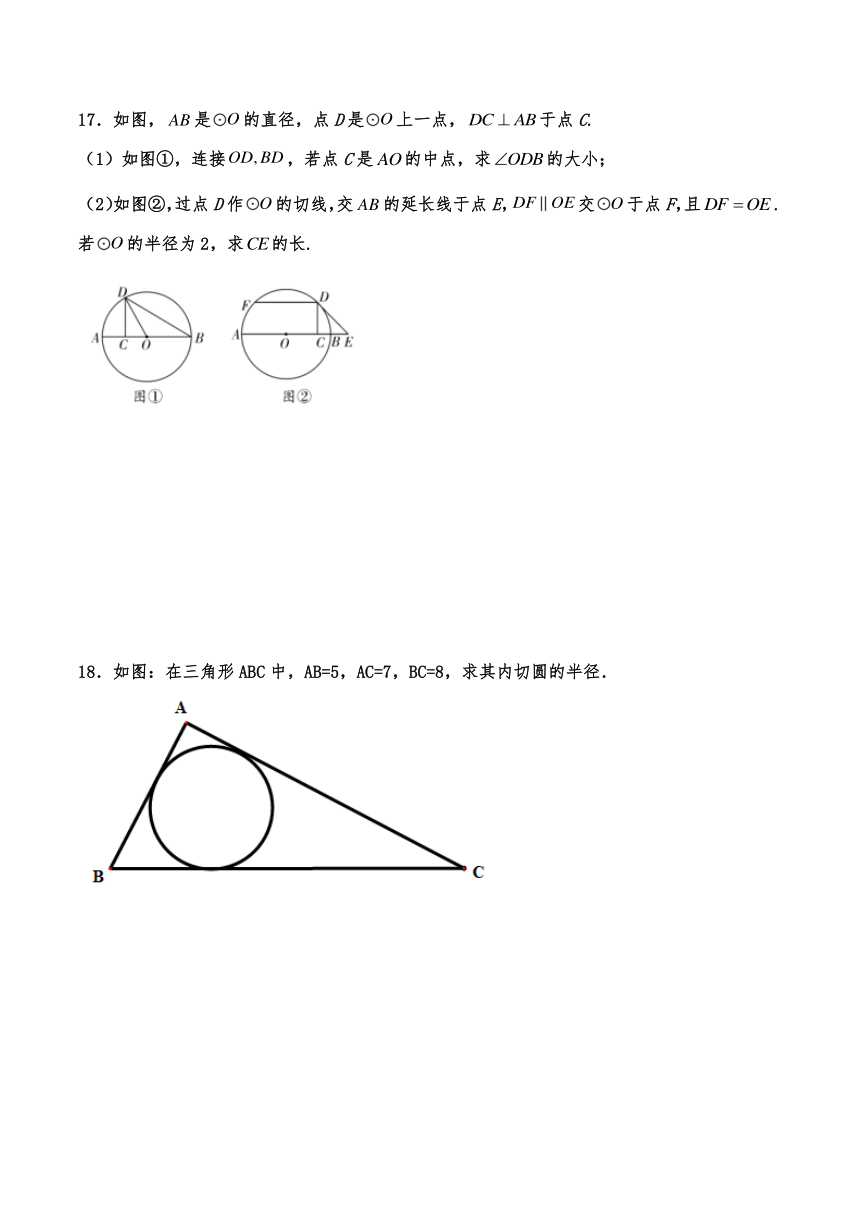
17.如图,是的直径,点D是上一点,于点C.
(1)如图①,连接,若点C是的中点,求的大小;
(2)如图②,过点D作的切线,交的延长线于点E,交于点F,且.若的半径为2,求的长.
18.如图:在三角形ABC中,AB=5,AC=7,BC=8,求其内切圆的半径.
19.在同一平面直角坐标系中有6个点:
A(1,1),B( 3, 1),C( 3,1),D( 2, 2),E( 2, 3),F(0, 4).
(1)画出△ABC的外接圆P,则点D与P的位置关系___;
(2)△ABC的外接圆的半径=___,△ABC的内切圆的半径=___.
(3)若将直线EF沿y轴向上平移,当它经过点D时,设此时的直线为,则直线与⊙P的位置关系____
20.如图,在中,,,是其内部一点,平分,连接,在上取一点,使,连接.
(1)求证:≌;
(2)若,连接,求的度数;
(3)若是的内心,过作于,求的取值范围.
答案
一、单选题
B.C.C.D.A.A.C.A.
二、填空题
9.到角两边距离相等的点在角平分线上;两点确定一条直线;角平分上的点到角两边的距离相等;圆的定义;经过半径的外端,并且垂直于这条半径的直线是圆的切线.
10.1:2.5
11.r=
12.60
13.2
14.140 125
三、解答题
15.
解:如图,在上取点,连接
四边形为的内接四边形,
为的内心,
分别平分
16.
解:连接OD.
∵AB=2DE,AB=2OD,∴OD=DE,
∴∠DOE=∠E=20°,∴∠CDO=∠DOE+∠E=40°,
∵OC=OD,∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
17.
解:(I)如图,连接,
∵点C是的中点,
∴,
∵,
∴,
∵,
∴,
∴为等边三角形,
∴,
∴,
∵,
∴.
(2)如图,连接,
∵为的切线,
∴,
∵,
∴四边形为平行四边形,
∴,
∴为等腰直角三角形,
∴,
∵,
∴.
18.
如图,作,设,则,
由勾股定理可知:,
则,解得,则,
故,
由三角形的内切圆性质,可得:
.
19.
(1)画出△ABC的外接圆P,如图所示,
∵,
∴点D与P的位置关系是点在圆上;
故答案为:在圆上;
(2)△ABC的外接圆的半径,△ABC的内切圆的半径为;
故答案为:;;
(3)画图之后由网格图得,直线与圆相交
故答案为:相交.
20.
解:(1)证明:∵,,,
∴≌.
(2)∵≌,
∴,,
∴,
∵,
∴.
(3)过作于,于,
∵是的内心,
∴,
∵,,
∴≌,
∴.
同理可得,,
∵,
∴,
∴,
∵,∴,
∴
一、单选题
1.如图,已知正方形ABCD的边长是8,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值是( )
A. B. C. D.
2.如图,在中,是直径,点是上一点,点是弧的中点,于点,过点的切线交的延长线于点,连接,分别交,于点.连接,关于下列结论:① ;②;③点是的外心,其中正确结论是( )
A.①② B.①③ C.②③ D.①②③
3.如图,把剪成三部分,边,,放在同一直线上,点都落在直线上,直线.在中,若,则的度数为( )
A. B. C. D.
4.一个等腰直角三角形的内切圆与外接圆的半径之比为( )
A. B. C. D.
5.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?“其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径”则该圆的直径为( )
A.6步 B.5步 C.4步 D.3步
6.下列关于三角形的内心说法正确的是( )
A.内心是三角形三条角平分线的交点
B.内心是三角形三边中垂线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )
A.128° B.126° C.122° D.120°
8.如图,的直径与弦的延长线交于点,若,,则=( )
A. B. C. D.
二、填空题
9.阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:求作:的内切圆.
小明的作法如下:如图2,
作,的平分线BE和CF,两线相交于点O;
过点O作,垂足为点D;
点O为圆心,OD长为半径作所以,即为所求作的圆.
请回答:该尺规作图的依据是______.
10.边长分别为3、4、5的三角形的内切圆半径与外接圆半径之比为________.
11.已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.
12.如图,已知点是的内心,若,则__________.
13.如图,在中,弦,点在上移动,连结,过点作交于点,则的最大值为__________.
14.在中,,若为的外心,则______度;若为的内心,则______度.
三、解答题
15.如图,点是外接圆的圆心,点是内切圆的圆心,已知,求和的度数.
16.如图所示,AB为☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
17.如图,是的直径,点D是上一点,于点C.
(1)如图①,连接,若点C是的中点,求的大小;
(2)如图②,过点D作的切线,交的延长线于点E,交于点F,且.若的半径为2,求的长.
18.如图:在三角形ABC中,AB=5,AC=7,BC=8,求其内切圆的半径.
19.在同一平面直角坐标系中有6个点:
A(1,1),B( 3, 1),C( 3,1),D( 2, 2),E( 2, 3),F(0, 4).
(1)画出△ABC的外接圆P,则点D与P的位置关系___;
(2)△ABC的外接圆的半径=___,△ABC的内切圆的半径=___.
(3)若将直线EF沿y轴向上平移,当它经过点D时,设此时的直线为,则直线与⊙P的位置关系____
20.如图,在中,,,是其内部一点,平分,连接,在上取一点,使,连接.
(1)求证:≌;
(2)若,连接,求的度数;
(3)若是的内心,过作于,求的取值范围.
答案
一、单选题
B.C.C.D.A.A.C.A.
二、填空题
9.到角两边距离相等的点在角平分线上;两点确定一条直线;角平分上的点到角两边的距离相等;圆的定义;经过半径的外端,并且垂直于这条半径的直线是圆的切线.
10.1:2.5
11.r=
12.60
13.2
14.140 125
三、解答题
15.
解:如图,在上取点,连接
四边形为的内接四边形,
为的内心,
分别平分
16.
解:连接OD.
∵AB=2DE,AB=2OD,∴OD=DE,
∴∠DOE=∠E=20°,∴∠CDO=∠DOE+∠E=40°,
∵OC=OD,∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
17.
解:(I)如图,连接,
∵点C是的中点,
∴,
∵,
∴,
∵,
∴,
∴为等边三角形,
∴,
∴,
∵,
∴.
(2)如图,连接,
∵为的切线,
∴,
∵,
∴四边形为平行四边形,
∴,
∴为等腰直角三角形,
∴,
∵,
∴.
18.
如图,作,设,则,
由勾股定理可知:,
则,解得,则,
故,
由三角形的内切圆性质,可得:
.
19.
(1)画出△ABC的外接圆P,如图所示,
∵,
∴点D与P的位置关系是点在圆上;
故答案为:在圆上;
(2)△ABC的外接圆的半径,△ABC的内切圆的半径为;
故答案为:;;
(3)画图之后由网格图得,直线与圆相交
故答案为:相交.
20.
解:(1)证明:∵,,,
∴≌.
(2)∵≌,
∴,,
∴,
∵,
∴.
(3)过作于,于,
∵是的内心,
∴,
∵,,
∴≌,
∴.
同理可得,,
∵,
∴,
∴,
∵,∴,
∴
