浙教版九年级数学下册试题 3.3 由三视图描述几何体同步习题(含答案)
文档属性
| 名称 | 浙教版九年级数学下册试题 3.3 由三视图描述几何体同步习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 299.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 14:04:44 | ||
图片预览

文档简介
3.3 由三视图描述几何体
一、选择题
1.一个几何体由若干个小正方体组成,其主视图和俯视图如图所示,若这个几何体中正方体的个数最多有个,最少有个,则的值为( )
A.10 B.11 C.12 D.9
2.一个几何体由大小相同的小立方块搭成,如图是从上面观察这个几何体得到的形状图,小正方形中的数字表示该位置上小立方块的个数,若要将该几何体补全成一个长方体,至少需添加同样的小立方块的个数为( )
A.4个 B.16个 C.24个 D.36个
3.物体的三视图是如图所示的三个图形,那么该物体形状是( )
A.长方体 B.圆锥体 C.立方体 D.圆柱体
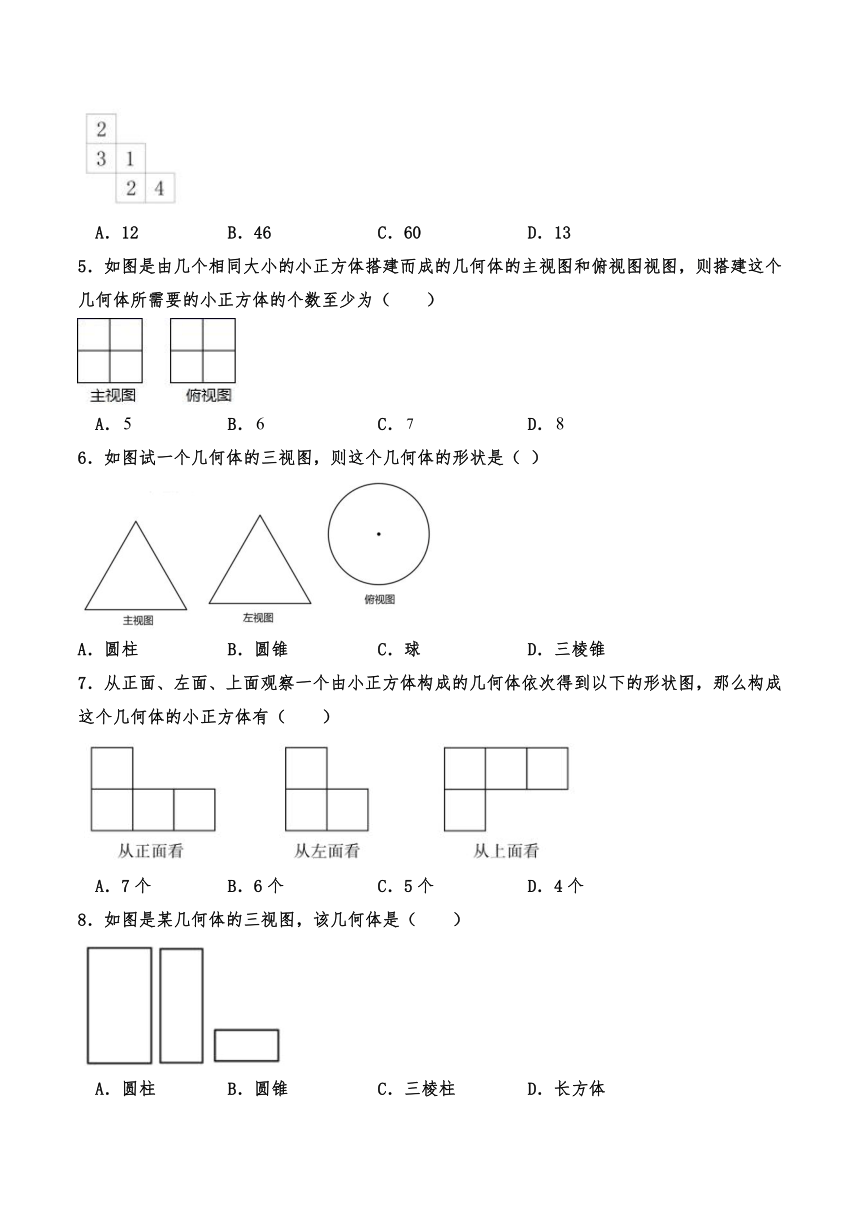
4.如图所示的是由几个棱长为1的小立方体块搭成的几何体从上往下看的平面图形,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的体积是( )
A.12 B.46 C.60 D.13
5.如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图视图,则搭建这个几何体所需要的小正方体的个数至少为( )
A. B. C. D.
6.如图试一个几何体的三视图,则这个几何体的形状是( )
A.圆柱 B.圆锥 C.球 D.三棱锥
7.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.7个 B.6个 C.5个 D.4个
8.如图是某几何体的三视图,该几何体是( )
A.圆柱 B.圆锥 C.三棱柱 D.长方体
二、填空题
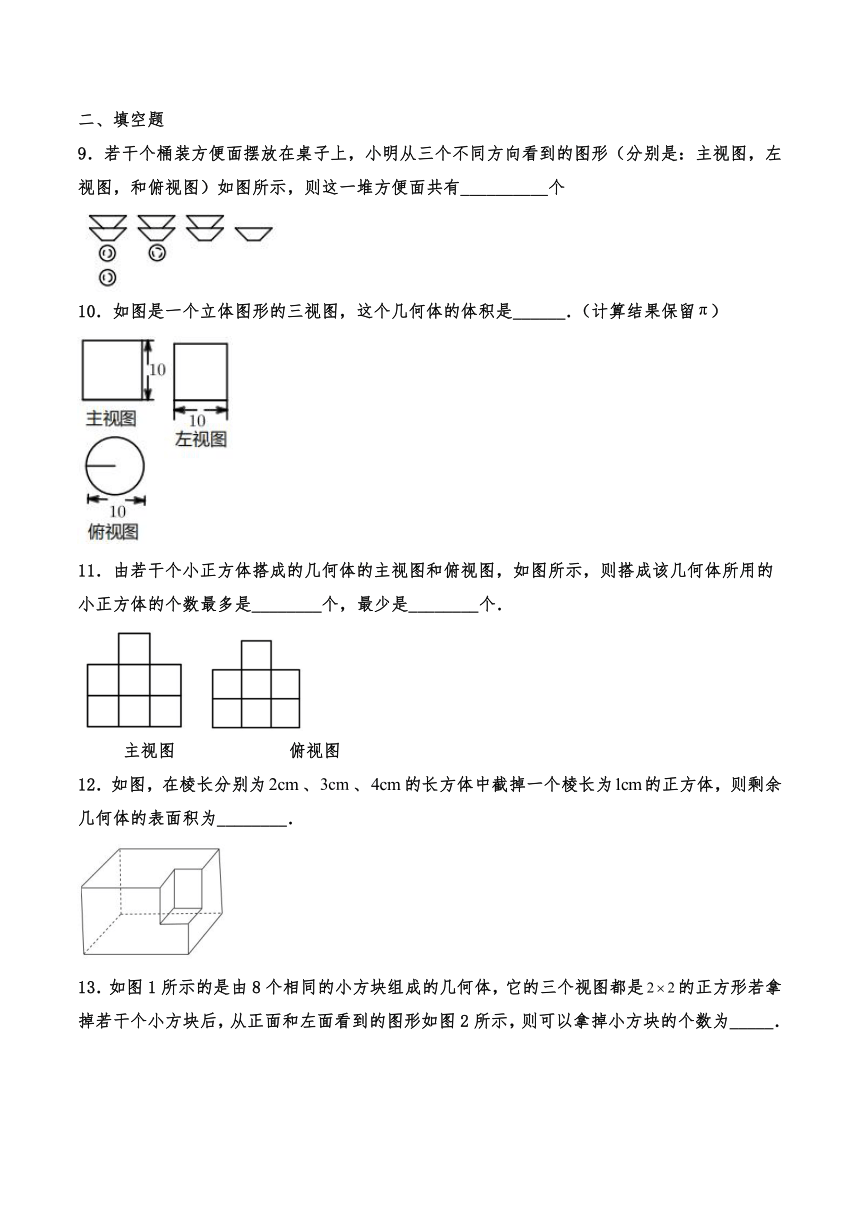
9.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形(分别是:主视图,左视图,和俯视图)如图所示,则这一堆方便面共有__________个
10.如图是一个立体图形的三视图,这个几何体的体积是______.(计算结果保留)
11.由若干个小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体所用的小正方体的个数最多是________个,最少是________个.
主视图 俯视图
12.如图,在棱长分别为、、的长方体中截掉一个棱长为的正方体,则剩余几何体的表面积为________.
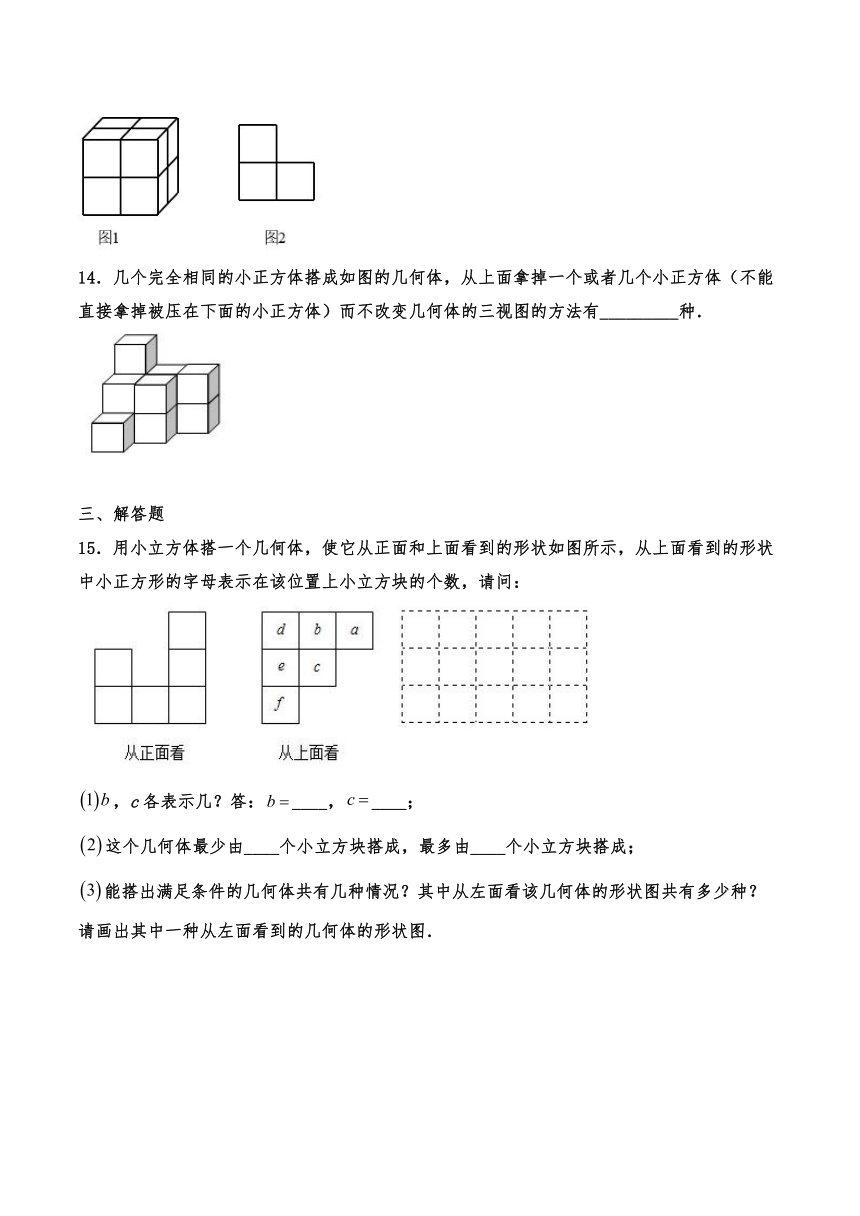
13.如图1所示的是由8个相同的小方块组成的几何体,它的三个视图都是的正方形若拿掉若干个小方块后,从正面和左面看到的图形如图2所示,则可以拿掉小方块的个数为_____.
14.几个完全相同的小正方体搭成如图的几何体,从上面拿掉一个或者几个小正方体(不能直接拿掉被压在下面的小正方体)而不改变几何体的三视图的方法有_________种.
三、解答题
15.用小立方体搭一个几何体,使它从正面和上面看到的形状如图所示,从上面看到的形状中小正方形的字母表示在该位置上小立方块的个数,请问:
,c各表示几?答:____,____;
这个几何体最少由____个小立方块搭成,最多由____个小立方块搭成;
能搭出满足条件的几何体共有几种情况?其中从左面看该几何体的形状图共有多少种?请画出其中一种从左面看到的几何体的形状图.
16.在桌面上,有若干个完全相同的小正方体堆成的一个几何体,如图所示.
(1)请依次画出从正面、左面、上面看这个几何体得到的形状图;
(2)如果保持从上面和正面观察到的形状图不变,那么最多可以添加______个小正方体.
17.如图是由几个相同的小立方体搭成的几何体从上面看到的形状图,小正方形中的数字表示在该位置的小立方体个数,画出这个几何体从正面看和左面看到的形状图.
18.用小立方体搭一个几何体,使它从正面看和从上面看的图形如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的图形.
19.如图所示.(V球=πr3).
(1)三个大小相同的球恰好放在一个圆柱形盒子里,三个球的体积占整个盒子容积的 (几分之几);
(2)若4个大小相同的球恰好放在一个圆柱形盒子里,4个球的体积占整个盒子容积的 (几分之几);
(3)m个大小相同的球恰好放在一个圆柱形盒子里,m个球的体积占整个盒子容积的 (几分之几).
20.在平整的地面上,有一个由若干个相同的小立方块搭成的几何体,如图所示.
(1)请依次画出从正面、左面、上面看这个几何体得到的图形;
(2)现在还有一些相同的小立方块,如果要保持从上面和左面看到的图形不变,那么最多可以添加几个这样的小立方块?
答案
一、选择题
B.C.D.A.B.B.C.D.
二、填空题
9.5
10.
11.17 11
12.
13.4或5
14.4
三、解答题
15.
(1)由主视图可知,第二列小立方体的个数均为1,那么,;
故答案为1,1;
(2)这个几何体最少由个小立方块搭成;
这个几何体最多由个小立方块搭成;
故答案为9,11;
(3)能搭出满足条件的几何体共有7种情况,其中从左面看该几何体的形状图共有4种,从左面看到的几何体的形状图如图所示:
.
16.
解:(1)如图所示:
(2)保持从上面和正面观察到的形状图不变,那么最多可以添加3个小立方块.
故答案为:3.
17.
解:如图所示:
18.
解:这样的几何体不只有一种,它最多需要2×3+2+3×2=14个小立方体,它最少需要3+1+2+2+2=10个小立方体.
小立方体最多时的左视图有3列,从左往右依次为2,3,3个正方形;
小立方体最少时的左视图有5种情况:①有3列,从左往右依次为1,1,3个正方形;②有3列,从左往右依次为1,2,3个正方形;③有3列,从左往右依次为2,1,3个正方形;④有3列,从左往右依次为1,3,2个正方形;⑤有3列,从左往右依次为2,3,2个正方形.
如图所示:
19.
解:(1)设球的半径为r,
根据题意得:三个球的体积之和=3×πr3=4πr3,
圆柱体盒子容积=πr2 6r=6πr3,
所以=.
即三个球的体积之和占整个盒子容积的;
(2)设球的半径为r,
根据题意得:四个球的体积之和=4×πr3=πr3,
圆柱体盒子容积=πr2 8r=8πr3,
所以=.
即四个球的体积之和占整个盒子容积的为;
(3)设球的半径为r,
根据题意得:m个球的体积之和=πr3=πr3,
圆柱体盒子容积=πr2 2mr=2mπr3,
所以=.
即m个球的体积之和占整个盒子容积的.
20.
解:(1)如图所示
(2)保持从上面看和从左面看所得图形不变,可往第二列的小正方体上各放一个小正方体,第3列的小正方体上放1个小正方体,
∴最多可以添加个这样的小立方块.
一、选择题
1.一个几何体由若干个小正方体组成,其主视图和俯视图如图所示,若这个几何体中正方体的个数最多有个,最少有个,则的值为( )
A.10 B.11 C.12 D.9
2.一个几何体由大小相同的小立方块搭成,如图是从上面观察这个几何体得到的形状图,小正方形中的数字表示该位置上小立方块的个数,若要将该几何体补全成一个长方体,至少需添加同样的小立方块的个数为( )
A.4个 B.16个 C.24个 D.36个
3.物体的三视图是如图所示的三个图形,那么该物体形状是( )
A.长方体 B.圆锥体 C.立方体 D.圆柱体
4.如图所示的是由几个棱长为1的小立方体块搭成的几何体从上往下看的平面图形,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的体积是( )
A.12 B.46 C.60 D.13
5.如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图视图,则搭建这个几何体所需要的小正方体的个数至少为( )
A. B. C. D.
6.如图试一个几何体的三视图,则这个几何体的形状是( )
A.圆柱 B.圆锥 C.球 D.三棱锥
7.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.7个 B.6个 C.5个 D.4个
8.如图是某几何体的三视图,该几何体是( )
A.圆柱 B.圆锥 C.三棱柱 D.长方体
二、填空题
9.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形(分别是:主视图,左视图,和俯视图)如图所示,则这一堆方便面共有__________个
10.如图是一个立体图形的三视图,这个几何体的体积是______.(计算结果保留)
11.由若干个小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体所用的小正方体的个数最多是________个,最少是________个.
主视图 俯视图
12.如图,在棱长分别为、、的长方体中截掉一个棱长为的正方体,则剩余几何体的表面积为________.
13.如图1所示的是由8个相同的小方块组成的几何体,它的三个视图都是的正方形若拿掉若干个小方块后,从正面和左面看到的图形如图2所示,则可以拿掉小方块的个数为_____.
14.几个完全相同的小正方体搭成如图的几何体,从上面拿掉一个或者几个小正方体(不能直接拿掉被压在下面的小正方体)而不改变几何体的三视图的方法有_________种.
三、解答题
15.用小立方体搭一个几何体,使它从正面和上面看到的形状如图所示,从上面看到的形状中小正方形的字母表示在该位置上小立方块的个数,请问:
,c各表示几?答:____,____;
这个几何体最少由____个小立方块搭成,最多由____个小立方块搭成;
能搭出满足条件的几何体共有几种情况?其中从左面看该几何体的形状图共有多少种?请画出其中一种从左面看到的几何体的形状图.
16.在桌面上,有若干个完全相同的小正方体堆成的一个几何体,如图所示.
(1)请依次画出从正面、左面、上面看这个几何体得到的形状图;
(2)如果保持从上面和正面观察到的形状图不变,那么最多可以添加______个小正方体.
17.如图是由几个相同的小立方体搭成的几何体从上面看到的形状图,小正方形中的数字表示在该位置的小立方体个数,画出这个几何体从正面看和左面看到的形状图.
18.用小立方体搭一个几何体,使它从正面看和从上面看的图形如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的图形.
19.如图所示.(V球=πr3).
(1)三个大小相同的球恰好放在一个圆柱形盒子里,三个球的体积占整个盒子容积的 (几分之几);
(2)若4个大小相同的球恰好放在一个圆柱形盒子里,4个球的体积占整个盒子容积的 (几分之几);
(3)m个大小相同的球恰好放在一个圆柱形盒子里,m个球的体积占整个盒子容积的 (几分之几).
20.在平整的地面上,有一个由若干个相同的小立方块搭成的几何体,如图所示.
(1)请依次画出从正面、左面、上面看这个几何体得到的图形;
(2)现在还有一些相同的小立方块,如果要保持从上面和左面看到的图形不变,那么最多可以添加几个这样的小立方块?
答案
一、选择题
B.C.D.A.B.B.C.D.
二、填空题
9.5
10.
11.17 11
12.
13.4或5
14.4
三、解答题
15.
(1)由主视图可知,第二列小立方体的个数均为1,那么,;
故答案为1,1;
(2)这个几何体最少由个小立方块搭成;
这个几何体最多由个小立方块搭成;
故答案为9,11;
(3)能搭出满足条件的几何体共有7种情况,其中从左面看该几何体的形状图共有4种,从左面看到的几何体的形状图如图所示:
.
16.
解:(1)如图所示:
(2)保持从上面和正面观察到的形状图不变,那么最多可以添加3个小立方块.
故答案为:3.
17.
解:如图所示:
18.
解:这样的几何体不只有一种,它最多需要2×3+2+3×2=14个小立方体,它最少需要3+1+2+2+2=10个小立方体.
小立方体最多时的左视图有3列,从左往右依次为2,3,3个正方形;
小立方体最少时的左视图有5种情况:①有3列,从左往右依次为1,1,3个正方形;②有3列,从左往右依次为1,2,3个正方形;③有3列,从左往右依次为2,1,3个正方形;④有3列,从左往右依次为1,3,2个正方形;⑤有3列,从左往右依次为2,3,2个正方形.
如图所示:
19.
解:(1)设球的半径为r,
根据题意得:三个球的体积之和=3×πr3=4πr3,
圆柱体盒子容积=πr2 6r=6πr3,
所以=.
即三个球的体积之和占整个盒子容积的;
(2)设球的半径为r,
根据题意得:四个球的体积之和=4×πr3=πr3,
圆柱体盒子容积=πr2 8r=8πr3,
所以=.
即四个球的体积之和占整个盒子容积的为;
(3)设球的半径为r,
根据题意得:m个球的体积之和=πr3=πr3,
圆柱体盒子容积=πr2 2mr=2mπr3,
所以=.
即m个球的体积之和占整个盒子容积的.
20.
解:(1)如图所示
(2)保持从上面看和从左面看所得图形不变,可往第二列的小正方体上各放一个小正方体,第3列的小正方体上放1个小正方体,
∴最多可以添加个这样的小立方块.
