浙教版九年级数学下册3.4 简单几何体的表面展开图 同步测试(含答案)
文档属性
| 名称 | 浙教版九年级数学下册3.4 简单几何体的表面展开图 同步测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 266.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 15:29:40 | ||
图片预览


文档简介
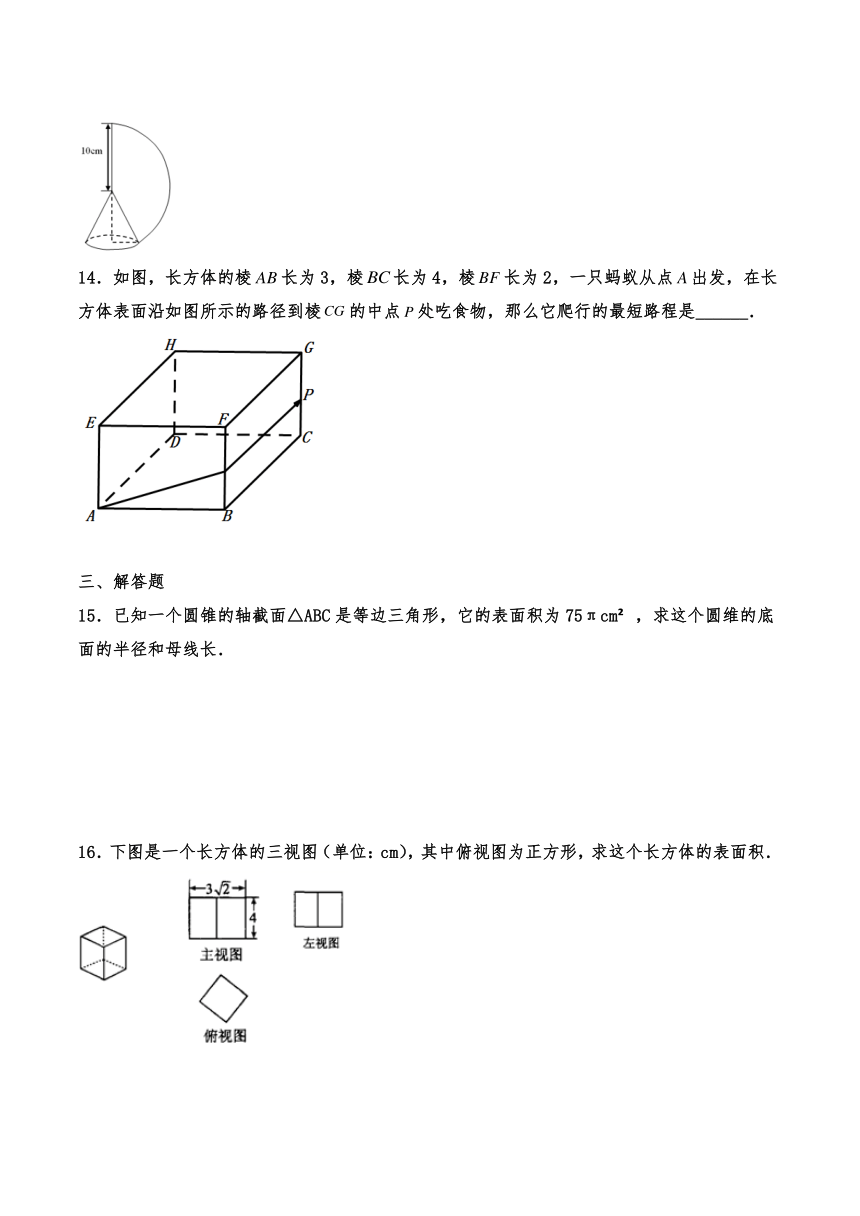
3.4 简单几何体的表面展开图
一、选择题
1.若圆锥的母线长20cm,底面圆的直径长10cm,则此圆锥侧面展开图的圆心角的度数是( )
A.30° B.60° C.90° D.180°
2.为落实好扶贫工作,某村驻村干部帮助村民修建了一个粮仓,该粮仓的屋顶是一个圆锥,为了合理购买、不浪费原材料,需要进行计算1个屋顶的侧面积大小,该圆锥母线长为5m,底面圆周长为,则1个屋顶的侧面积等于( ).(结果保留)
A. B. C. D.
3.有一个棱长为5的正方体木块,从它的每一个面看都有一个穿透的完全相同的孔(如图中的阴影部分),则这个立体图形的内、外表面的总面积是 ( )
A.192 B.216 C.218 D.225
4.若圆锥的底面半径为,侧面积为,则该圆锥的高是( )
A. B. C. D.
5.一个圆锥的底面直径为4 cm,其侧面展开后是圆心角为90°的扇形,则这个圆锥的侧面积等于( )
A.4πcm2 B.8πcm2 C.12πcm2 D.16πcm2
6.已知圆锥的底面半径为3cm,母线长为6cm,则圆锥的侧面积是( )
A.18cm2 B. C.27cm2 D.
7.如图是某工件的三视图.则此工件的表面积为( )
A.20πcm2 B.36πcm2 C.56πcm2 D.24πcm2
8.如图,矩形的长与宽分别为a和b,在矩形中截取两个大小相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成一个没有空隙的圆柱,则a和b要满足的数量关系是( )
A. B. C. D.
二、填空题
9.圆锥的侧面展开图是一个扇形,扇形的弧长为10π cm,扇形面积为65π cm2,则圆锥的高为______cm.
10.小红在手工制作课上,用面积为,半径为的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为_______.
11.已知圆锥的轴截面是边长为6的等边三角形,则这个圆锥侧面展开图的圆心角为______度.
12.圆锥的侧面展开图的面积为,母线长为3,则该圆锥的底面半径为_________.
13.如图,用一张半径为10cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的高为8cm,那么这张扇形纸板的弧长是_______cm,制作这个帽子需要的纸板的面积为_______cm2.
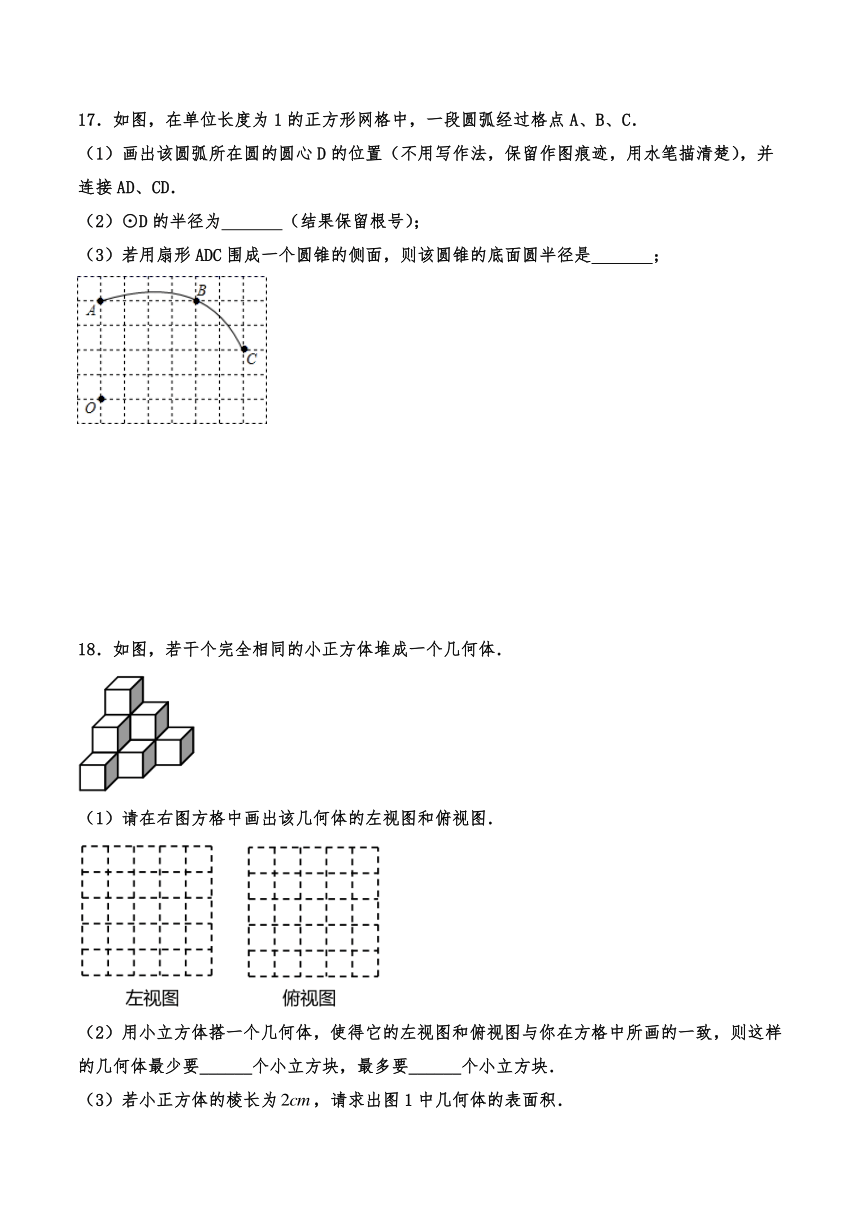
14.如图,长方体的棱长为3,棱长为4,棱长为2,一只蚂蚁从点出发,在长方体表面沿如图所示的路径到棱的中点处吃食物,那么它爬行的最短路程是______.
三、解答题
15.已知一个圆锥的轴截面△ABC是等边三角形,它的表面积为75πcm ,求这个圆维的底面的半径和母线长.
16.下图是一个长方体的三视图(单位:cm),其中俯视图为正方形,求这个长方体的表面积.
17.如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
(1)画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹,用水笔描清楚),并连接AD、CD.
(2)⊙D的半径为 (结果保留根号);
(3)若用扇形ADC围成一个圆锥的侧面,则该圆锥的底面圆半径是 ;
18.如图,若干个完全相同的小正方体堆成一个几何体.
(1)请在右图方格中画出该几何体的左视图和俯视图.
(2)用小立方体搭一个几何体,使得它的左视图和俯视图与你在方格中所画的一致,则这样的几何体最少要______个小立方块,最多要______个小立方块.
(3)若小正方体的棱长为,请求出图1中几何体的表面积.
19.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a,2的对面数字为b,那么a+b的值为_____.
20.已知图为一几何体从不同方向看的图形:
(1)写出这几个几何体的名称;
(2)若长方形的高为10厘米,三角形的边长为4厘米,求这个几何体的侧面积.
答案
一、选择题
C.B.B.B.D.B.B.D.
二、填空题
9.12
10.1
11.180
12.2.
13.12π 60π
14.
三、解答题
15.解:设这个圆锥的底面半径为rcm,
∵圆锥的轴截面△ABC是等边三角形,∴圆锥母线的长为2rcm,
∵圆锥的母线即为扇形半径,圆锥底面圆的周长等于扇形弧长,扇形面积+底面圆的面积=圆锥表面积.
∴×2πr×2r+πr2=75π,
解得:r=5,∴2r=10.
故这个圆锥的底面半径为5cm,母线长为10cm.
16.
解:如图所示:AB=3,
∵AC2+BC2=AB2,
∴AC=BC=3,
∴正方形ACBD面积为:3×3=9,
侧面积为:4AC×CE=3×4×4=48,
故这个长方体的表面积为:48+9+9=.
17.
解:(1)
(2)⊙D的半径AD
(3)根据图上信息,可知道
的长度l= =
扇形ADC围成一个圆锥的侧面,则圆锥的底面圆周长等于弧长的长度.
圆锥的底面圆半径
18.
解:(1)如图所示:
(2)由俯视图易得最底层有6个小正方体,第二层最少有2个小正方体,第三层最少有1个小正方体,所以最少有个小正方体;
由俯视图易得最底层有6个小正方体,第二层最多有5个小正方体,第三层最多有3个小正方体,所以最多有个小正方体.
故答案为:9,14;
(3)这个几何体的表面积为:.
19.
一个正方体已知1,4,6,第二个正方体已知1,2,3,第三个正方体已知2,5,6,且不同的面上写的数字各不相同,可求得1的对面数字为5,6的对面数字为3,2的对面数字为4
∴a+b=7
故答案为:7.
20.
(1)∵主视图和左视图是长方形,根据俯视图是正三角形,
∴这个几何体为正三棱柱;
(2)3×10×4=120(cm2),
答:这个几何体的侧面积为120cm2.
一、选择题
1.若圆锥的母线长20cm,底面圆的直径长10cm,则此圆锥侧面展开图的圆心角的度数是( )
A.30° B.60° C.90° D.180°
2.为落实好扶贫工作,某村驻村干部帮助村民修建了一个粮仓,该粮仓的屋顶是一个圆锥,为了合理购买、不浪费原材料,需要进行计算1个屋顶的侧面积大小,该圆锥母线长为5m,底面圆周长为,则1个屋顶的侧面积等于( ).(结果保留)
A. B. C. D.
3.有一个棱长为5的正方体木块,从它的每一个面看都有一个穿透的完全相同的孔(如图中的阴影部分),则这个立体图形的内、外表面的总面积是 ( )
A.192 B.216 C.218 D.225
4.若圆锥的底面半径为,侧面积为,则该圆锥的高是( )
A. B. C. D.
5.一个圆锥的底面直径为4 cm,其侧面展开后是圆心角为90°的扇形,则这个圆锥的侧面积等于( )
A.4πcm2 B.8πcm2 C.12πcm2 D.16πcm2
6.已知圆锥的底面半径为3cm,母线长为6cm,则圆锥的侧面积是( )
A.18cm2 B. C.27cm2 D.
7.如图是某工件的三视图.则此工件的表面积为( )
A.20πcm2 B.36πcm2 C.56πcm2 D.24πcm2
8.如图,矩形的长与宽分别为a和b,在矩形中截取两个大小相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成一个没有空隙的圆柱,则a和b要满足的数量关系是( )
A. B. C. D.
二、填空题
9.圆锥的侧面展开图是一个扇形,扇形的弧长为10π cm,扇形面积为65π cm2,则圆锥的高为______cm.
10.小红在手工制作课上,用面积为,半径为的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为_______.
11.已知圆锥的轴截面是边长为6的等边三角形,则这个圆锥侧面展开图的圆心角为______度.
12.圆锥的侧面展开图的面积为,母线长为3,则该圆锥的底面半径为_________.
13.如图,用一张半径为10cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的高为8cm,那么这张扇形纸板的弧长是_______cm,制作这个帽子需要的纸板的面积为_______cm2.
14.如图,长方体的棱长为3,棱长为4,棱长为2,一只蚂蚁从点出发,在长方体表面沿如图所示的路径到棱的中点处吃食物,那么它爬行的最短路程是______.
三、解答题
15.已知一个圆锥的轴截面△ABC是等边三角形,它的表面积为75πcm ,求这个圆维的底面的半径和母线长.
16.下图是一个长方体的三视图(单位:cm),其中俯视图为正方形,求这个长方体的表面积.
17.如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
(1)画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹,用水笔描清楚),并连接AD、CD.
(2)⊙D的半径为 (结果保留根号);
(3)若用扇形ADC围成一个圆锥的侧面,则该圆锥的底面圆半径是 ;
18.如图,若干个完全相同的小正方体堆成一个几何体.
(1)请在右图方格中画出该几何体的左视图和俯视图.
(2)用小立方体搭一个几何体,使得它的左视图和俯视图与你在方格中所画的一致,则这样的几何体最少要______个小立方块,最多要______个小立方块.
(3)若小正方体的棱长为,请求出图1中几何体的表面积.
19.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a,2的对面数字为b,那么a+b的值为_____.
20.已知图为一几何体从不同方向看的图形:
(1)写出这几个几何体的名称;
(2)若长方形的高为10厘米,三角形的边长为4厘米,求这个几何体的侧面积.
答案
一、选择题
C.B.B.B.D.B.B.D.
二、填空题
9.12
10.1
11.180
12.2.
13.12π 60π
14.
三、解答题
15.解:设这个圆锥的底面半径为rcm,
∵圆锥的轴截面△ABC是等边三角形,∴圆锥母线的长为2rcm,
∵圆锥的母线即为扇形半径,圆锥底面圆的周长等于扇形弧长,扇形面积+底面圆的面积=圆锥表面积.
∴×2πr×2r+πr2=75π,
解得:r=5,∴2r=10.
故这个圆锥的底面半径为5cm,母线长为10cm.
16.
解:如图所示:AB=3,
∵AC2+BC2=AB2,
∴AC=BC=3,
∴正方形ACBD面积为:3×3=9,
侧面积为:4AC×CE=3×4×4=48,
故这个长方体的表面积为:48+9+9=.
17.
解:(1)
(2)⊙D的半径AD
(3)根据图上信息,可知道
的长度l= =
扇形ADC围成一个圆锥的侧面,则圆锥的底面圆周长等于弧长的长度.
圆锥的底面圆半径
18.
解:(1)如图所示:
(2)由俯视图易得最底层有6个小正方体,第二层最少有2个小正方体,第三层最少有1个小正方体,所以最少有个小正方体;
由俯视图易得最底层有6个小正方体,第二层最多有5个小正方体,第三层最多有3个小正方体,所以最多有个小正方体.
故答案为:9,14;
(3)这个几何体的表面积为:.
19.
一个正方体已知1,4,6,第二个正方体已知1,2,3,第三个正方体已知2,5,6,且不同的面上写的数字各不相同,可求得1的对面数字为5,6的对面数字为3,2的对面数字为4
∴a+b=7
故答案为:7.
20.
(1)∵主视图和左视图是长方形,根据俯视图是正三角形,
∴这个几何体为正三棱柱;
(2)3×10×4=120(cm2),
答:这个几何体的侧面积为120cm2.
