二次函数的图象与性质复习1(浙江省宁波市)
文档属性
| 名称 | 二次函数的图象与性质复习1(浙江省宁波市) |  | |
| 格式 | rar | ||
| 文件大小 | 221.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-04 19:55:00 | ||
图片预览


文档简介
课件18张PPT。二次函数的图象与性质
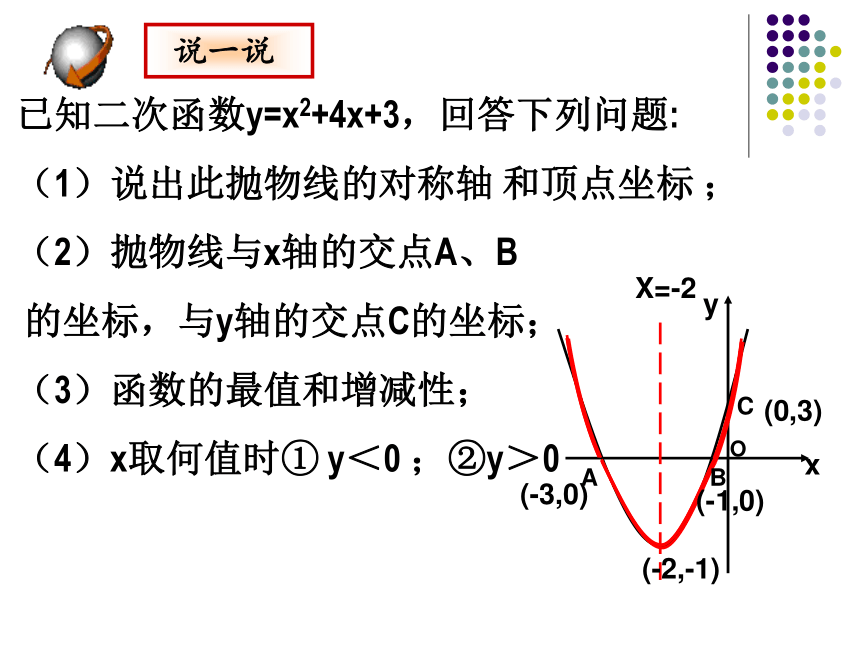
(复习一)已知二次函数y=x2+4x+3,回答下列问题:
(1)说出此抛物线的对称轴 和顶点坐标 ;
(2)抛物线与x轴的交点A、B
的坐标,与y轴的交点C的坐标;
(3)函数的最值和增减性;
(4)x取何值时① y<0 ;②y>0
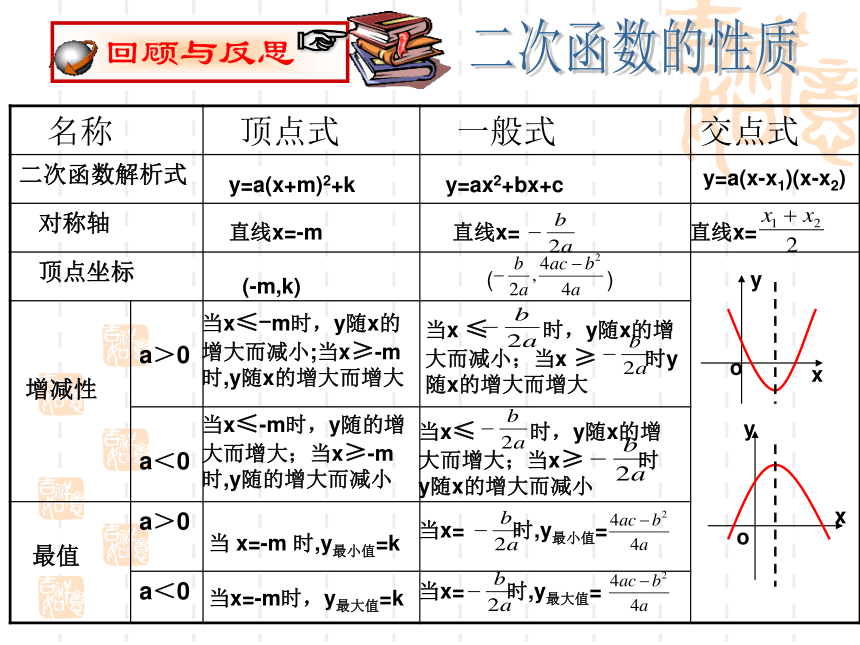
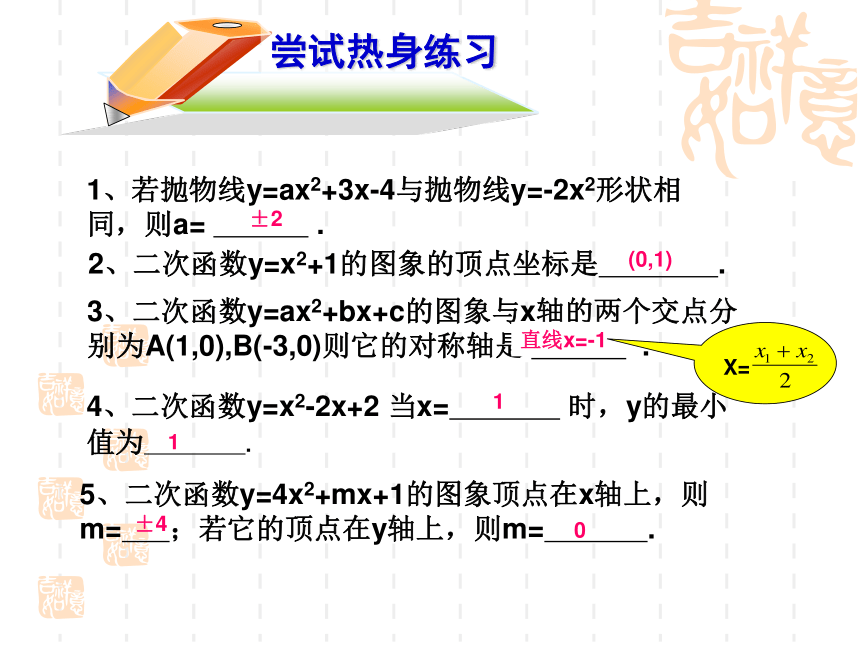
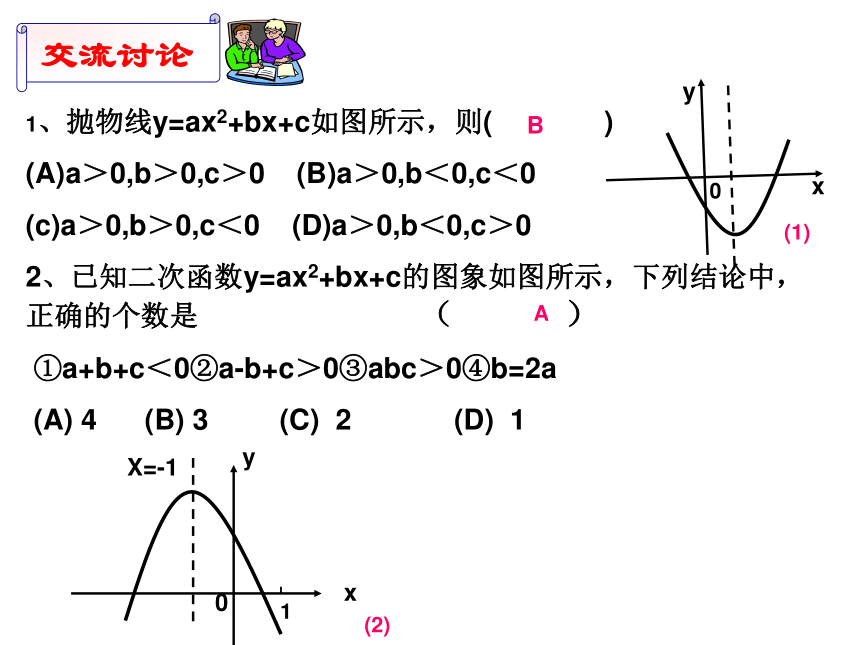
xyABOCX=-2(-3,0)(-1,0)(-2,-1)(0,3) 说一说二次函数的性质y=a(x+m)2+ky=ax2+bx+cy=a(x-x1)(x-x2)直线x=-m直线x=直线x=(-m,k)( ) 当x≤-m时,y随x的增大而减小;当x≥-m时,y随x的增大而增大当x ≤ 时,y随x的增大而减小;当x ≥ 时y随x的增大而增大当x≤-m时,y随的增大而增大;当x≥-m时,y随的增大而减小当x≤ 时,y随x的增大而增大;当x≥ 时y随x的增大而减小当 x=-m 时,y最小值=k当x= 时,y最小值=当x=-m时,y最大值=k当x= 时,y最大值=yxooyx1、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同,则a= .2、二次函数y=x2+1的图象的顶点坐标是 .3、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .4、二次函数y=x2-2x+2 当x= 时,y的最小值为 .5、二次函数y=4x2+mx+1的图象顶点在x轴上,则m= ;若它的顶点在y轴上,则m= .±2(0,1)直线x=-111±40X=1、抛物线y=ax2+bx+c如图所示,则( )
(A)a>0,b>0,c>0 (B)a>0,b<0,c<0
(c)a>0,b>0,c<0 (D)a>0,b<0,c>0
2、已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的个数是 ( )
①a+b+c<0②a-b+c>0③abc>0④b=2a
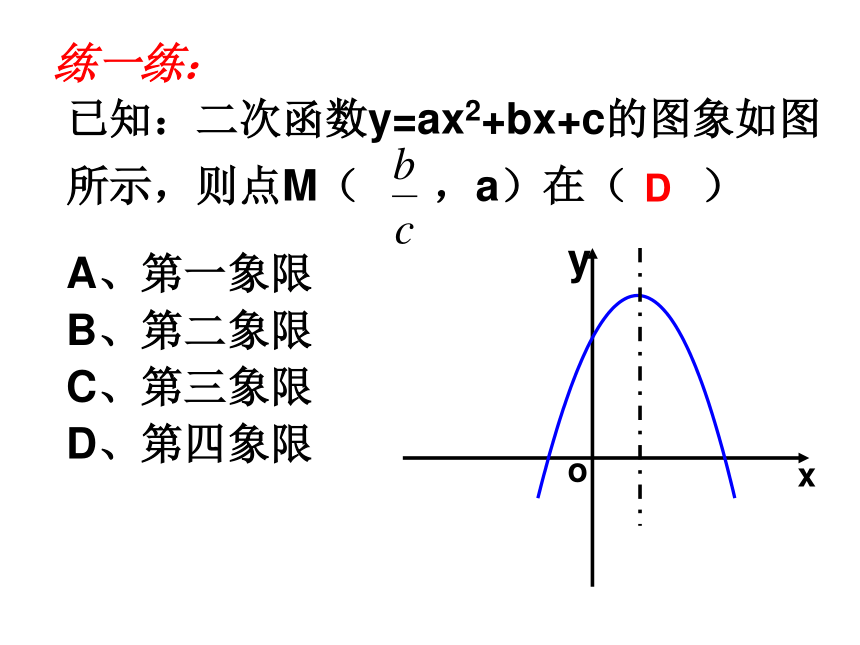
(A) 4 (B) 3 (C) 2 (D) 1xyxyX=-10(2)(1)BC1A看方向 (上正、下负)看交点 (上正、下负)二次函数的图象看对称轴(左同、右异) 练一练:已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD 练习:在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为答案: B二次函数应用解题步骤:
第一步设自变量;
第二步建立函数的解析式;
第三步确定自变量的取值范围;
第四步根据顶点坐标公式或配方法求出最大值或最小值(在自变量的取值范围内) 例1、某商人如果将进货单价为8元的商品按每件10元出售,每天可销售100件,现在他采用提高出售价格,减少进货量的办法增加利润,已知这种商品每涨价一元,其销售量将减少10件,问他将出售价定为多少元时,才能使每天所获利润最大?并且求出最大利润是多少?解:设利润为y元,售价为x元,则每天可销售100-10(x-10)件,依题意得:
y=(x-8)([100-10(x-10)]
化简得
y= -10x2-280x -1600
配方得
y= -10(x-14)2 + 360
∴当 (x-14)2 =0时,即x=14时,y 有最大值是360
答:当定价为14元时,所获利润最大,最大利润是360元。 典型例题典型例题 例2:等腰直角三角形以2米/秒的速度沿直线向边长为4cm的正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y平方米.
(1)写出y与x的函数关系式及自变量的取值范围
(2)当重叠部分的面积是正方形的面积的一半时,三角形移动了多长时间?思考:如果继续向前移动,则重叠部分面积又会如何变化?探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
已知:如图,二次函数 的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的顶点为P.
(1)求A、B两点的坐标;
(2)求证:AP∥CB;
(3)若∠CBP=60o,求抛物线的解析式. 1、已知对于x的所有实数,函数y=x2-4kx+2k+30的值均为非负数,化简:2、已知抛物线y=(m-1)x2+4x-3开口向上,与x轴相交于A(x1,0)和B(x2,0)两点,其中x1<x2
(1)求m的取值范围;
(2)若x12+x22=10,求抛物线的解析式,并在平面直角坐标系中画出这条抛物线;
(3)设这条抛物线的顶点坐标为C,延长CA交y轴于点D。在y轴上是否存在点P,使以P、O、B为顶点的三角形与△BCD相似?若存在,求出P点的坐标;若不存在,请说明理由。例:已知抛物线y=x2+(2n-1)x+n2-1(n为常数)
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数解析式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C。
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请你求出这个最大值,并指出此时A点的坐标;如果不存在,请说出你的理由。 尝试拓展 发展思维?行家看“门道”(1)通过本节课的学习你对二次函数的图象与性质有什么的认识?
(复习一)已知二次函数y=x2+4x+3,回答下列问题:
(1)说出此抛物线的对称轴 和顶点坐标 ;
(2)抛物线与x轴的交点A、B
的坐标,与y轴的交点C的坐标;
(3)函数的最值和增减性;
(4)x取何值时① y<0 ;②y>0
xyABOCX=-2(-3,0)(-1,0)(-2,-1)(0,3) 说一说二次函数的性质y=a(x+m)2+ky=ax2+bx+cy=a(x-x1)(x-x2)直线x=-m直线x=直线x=(-m,k)( ) 当x≤-m时,y随x的增大而减小;当x≥-m时,y随x的增大而增大当x ≤ 时,y随x的增大而减小;当x ≥ 时y随x的增大而增大当x≤-m时,y随的增大而增大;当x≥-m时,y随的增大而减小当x≤ 时,y随x的增大而增大;当x≥ 时y随x的增大而减小当 x=-m 时,y最小值=k当x= 时,y最小值=当x=-m时,y最大值=k当x= 时,y最大值=yxooyx1、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同,则a= .2、二次函数y=x2+1的图象的顶点坐标是 .3、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .4、二次函数y=x2-2x+2 当x= 时,y的最小值为 .5、二次函数y=4x2+mx+1的图象顶点在x轴上,则m= ;若它的顶点在y轴上,则m= .±2(0,1)直线x=-111±40X=1、抛物线y=ax2+bx+c如图所示,则( )
(A)a>0,b>0,c>0 (B)a>0,b<0,c<0
(c)a>0,b>0,c<0 (D)a>0,b<0,c>0
2、已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的个数是 ( )
①a+b+c<0②a-b+c>0③abc>0④b=2a
(A) 4 (B) 3 (C) 2 (D) 1xyxyX=-10(2)(1)BC1A看方向 (上正、下负)看交点 (上正、下负)二次函数的图象看对称轴(左同、右异) 练一练:已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD 练习:在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为答案: B二次函数应用解题步骤:
第一步设自变量;
第二步建立函数的解析式;
第三步确定自变量的取值范围;
第四步根据顶点坐标公式或配方法求出最大值或最小值(在自变量的取值范围内) 例1、某商人如果将进货单价为8元的商品按每件10元出售,每天可销售100件,现在他采用提高出售价格,减少进货量的办法增加利润,已知这种商品每涨价一元,其销售量将减少10件,问他将出售价定为多少元时,才能使每天所获利润最大?并且求出最大利润是多少?解:设利润为y元,售价为x元,则每天可销售100-10(x-10)件,依题意得:
y=(x-8)([100-10(x-10)]
化简得
y= -10x2-280x -1600
配方得
y= -10(x-14)2 + 360
∴当 (x-14)2 =0时,即x=14时,y 有最大值是360
答:当定价为14元时,所获利润最大,最大利润是360元。 典型例题典型例题 例2:等腰直角三角形以2米/秒的速度沿直线向边长为4cm的正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y平方米.
(1)写出y与x的函数关系式及自变量的取值范围
(2)当重叠部分的面积是正方形的面积的一半时,三角形移动了多长时间?思考:如果继续向前移动,则重叠部分面积又会如何变化?探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
已知:如图,二次函数 的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的顶点为P.
(1)求A、B两点的坐标;
(2)求证:AP∥CB;
(3)若∠CBP=60o,求抛物线的解析式. 1、已知对于x的所有实数,函数y=x2-4kx+2k+30的值均为非负数,化简:2、已知抛物线y=(m-1)x2+4x-3开口向上,与x轴相交于A(x1,0)和B(x2,0)两点,其中x1<x2
(1)求m的取值范围;
(2)若x12+x22=10,求抛物线的解析式,并在平面直角坐标系中画出这条抛物线;
(3)设这条抛物线的顶点坐标为C,延长CA交y轴于点D。在y轴上是否存在点P,使以P、O、B为顶点的三角形与△BCD相似?若存在,求出P点的坐标;若不存在,请说明理由。例:已知抛物线y=x2+(2n-1)x+n2-1(n为常数)
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数解析式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C。
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请你求出这个最大值,并指出此时A点的坐标;如果不存在,请说出你的理由。 尝试拓展 发展思维?行家看“门道”(1)通过本节课的学习你对二次函数的图象与性质有什么的认识?
同课章节目录
