中位线教案

7.3.5中位线
【教学目标】
1． 能准确地掌握三角形、梯形的中位线定理。
2．能运用中位线解决中点四边形问题。
3．通过定理的证明与应用提高分析问题、解决问题的能力。
【教学重点、难点】
教学重点：理解三角形、梯形的中位线定理以及定理的应用。
教学难点：进一步领会把未知问题转化为已知问题的思想方法。
【教学准备】
多媒体课件
【教学过程】
一．情景引入
你知道中间的菱形与矩形是怎样设计出来的吗？
二．新课教学
1． 复习三角形的中位线的概念与定理（证明定理）
定义：连结三角形两边中点的线段叫做三角形的中位线。
定理： 三角形的中位线平行于第三边，并且等于第三边的一半。
2． 复习梯形的中位线的概念与定理（证明定理）
定义：连结梯形的两腰的中点的线段叫做梯形的中位线。
定理：梯形的中位线平行于两底边，并且等于两底边和的一半。
3． 应用
（1） 任意画一个四边形，依次连接四边中点，你能得到什么图形？
（2） 观察下图的变化过程，顺次连接任意四边形四边中点所得的是什么图形？试证明你的发现。
结论：顺次连接任意四边形四边中点所得的图形是平行四边形。
（3）回顾刚才的证明过程，得到的平行四边形的边长取决于谁的长度？
（4）如果原四边形的对角线相等，则得到的图形四边有何关系？由此你发现了什么？证明你的发现。
结论：如果四边形的对角线相等，那么顺次连接各边中点所得到的图形是菱形。
（5）设问：平行四边形EFGH的每个角取决于什么，为什么？
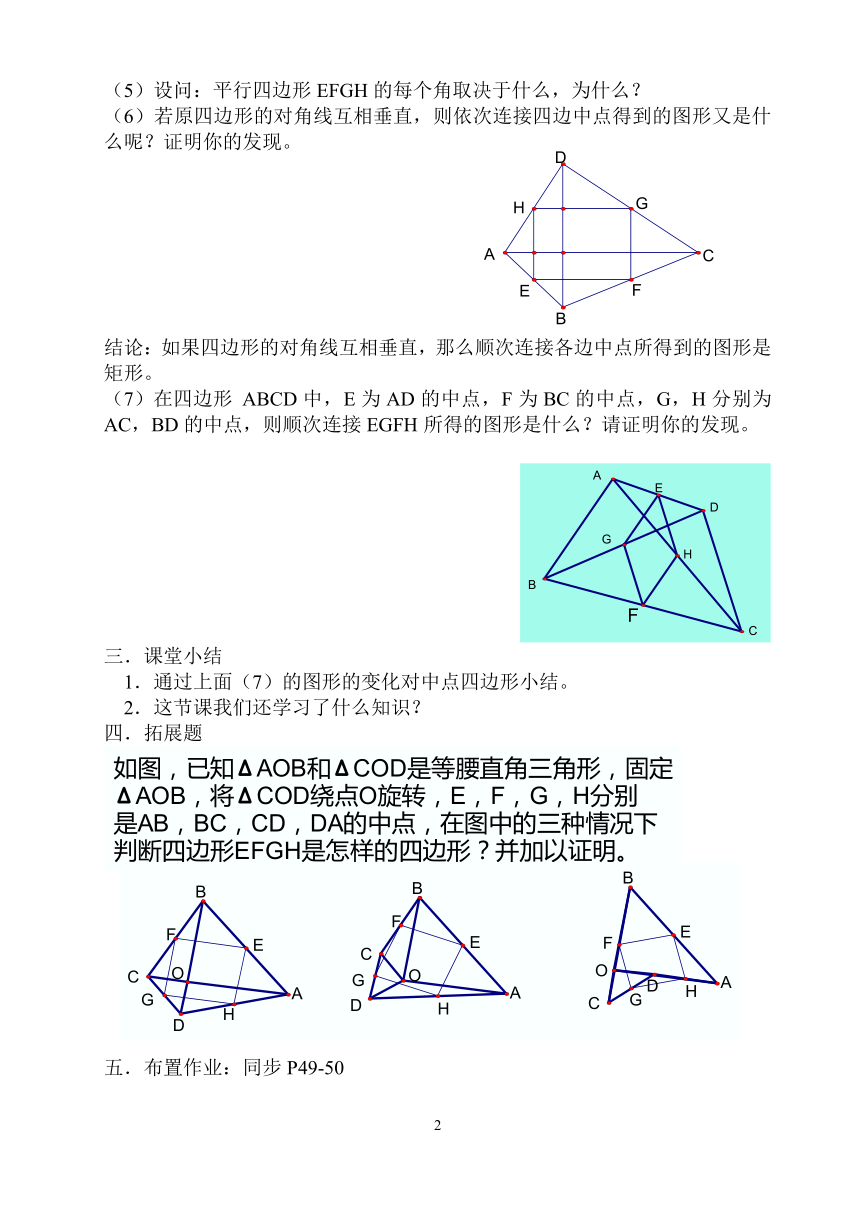
（6）若原四边形的对角线互相垂直，则依次连接四边中点得到的图形又是什么呢？证明你的发现。
结论：如果四边形的对角线互相垂直，那么顺次连接各边中点所得到的图形是矩形。
（7）在四边形 ABCD中，E为AD的中点，F为BC的中点，G，H分别为AC，BD的中点，则顺次连接EGFH所得的图形是什么？请证明你的发现。
三．课堂小结
1． 通过上面（7）的图形的变化对中点四边形小结。
2． 这节课我们还学习了什么知识？
四．拓展题
五．布置作业：同步P49-50
练习题
一．填空：
1．一个梯形的中位线的长是高的2倍，面积是18平方厘米，则这个梯形的高是 。
2．等腰梯形的中位线的长为6厘米，腰长为4厘米，则它的周长是 。
3． 如图，EF是△ABC的中位线，AD是△ABC的中线，
则EF与AD的关系 。
一.解答题
1． 已知，如图，在正方形ABCD中，AC、BD相交于点O，
AE平分∠BAC，分别交BC、BO于点E、F。求证：OF=CE。
2.已知，如图，△ABC中，BM，CN平分∠BAC，∠ACB的外角，AM⊥BM于点M，AN⊥CN于点N。
求证：MN=（AB+AC+BC）
3．观察下图的变化过程，顺次连接任意四边形四边中点所得的是什么图形？试证明你的发现。
4．如果原四边形的对角线相等，则得到的图形四边有何关系？由此你发现了什么？证明你的发现。
5．若四边形的对角线互相垂直，则依次连接四边中点得到的图形又是什么呢？证明你的发现。
6．在四边形 ABCD中，E为AD的中点，F为B的中点，G，H分别为AC，BD的中点，则顺次连接EGFH所得的图形是什么？请证明你的发现。
7．
8.如图,AB=CD,AN=ND,BM=CM,
求证: ∠BFM=∠MEC
PAGE
1